2024年浙教版数学七年级下册期中仿真模拟卷(一)(范围:1-3章)
试卷更新日期:2024-04-16 类型:期中考试
一、选择题(每题3分,共30分)
-
1. 下列方程是二元一次方程的是( )A、 B、 C、 D、2. 的运算结果正确的时( )A、 B、 C、 D、3. 如图,的同位角是( )
 A、 B、 C、 D、4. 下列说法正确的是A、单项式的系数为 B、多项式的次数为3 C、单项式的次数为7 D、是整式5. 已知关于 , 的方程组 ,将此方程组的两个方程左右两边分别对应相加,得到一个新的方程,当 每取一个值时,就有一个方程,这些方程有一个公共解,这个公共解是( )A、 B、 C、 D、6. 如图,为一条长方形纸带, , 将沿折叠,A , D两点分别与 , 对应,若 , 则的度数是( )
A、 B、 C、 D、4. 下列说法正确的是A、单项式的系数为 B、多项式的次数为3 C、单项式的次数为7 D、是整式5. 已知关于 , 的方程组 ,将此方程组的两个方程左右两边分别对应相加,得到一个新的方程,当 每取一个值时,就有一个方程,这些方程有一个公共解,这个公共解是( )A、 B、 C、 D、6. 如图,为一条长方形纸带, , 将沿折叠,A , D两点分别与 , 对应,若 , 则的度数是( ) A、 B、 C、 D、7. 已知直线AB及AB外一点P,若过点P作一直线与AB平行,那么这样的直线( )A、有且只有一条 B、有两条 C、不存在 D、无数条8. 下列说法中,正确的是( )A、两条不相交的直线叫做平行线 B、在同一平面内,一条直线的平行线有无数条 C、在同一平面内,两条直线一定相交 D、经过一点有且只有一条直线与已 知直线平行9. 如图,在长方形ABCD中,AB=6,BC=10,其内部有边长为a的正方形AEFG与边长为b的正方形HIJK,两个正方形的重合部分也为正方形,且面积为5.若右侧阴影部分的面积S2是左侧阴影部分面积S1的4倍,则正方形AEFG与正方形HIJK的面积之和为( )
A、 B、 C、 D、7. 已知直线AB及AB外一点P,若过点P作一直线与AB平行,那么这样的直线( )A、有且只有一条 B、有两条 C、不存在 D、无数条8. 下列说法中,正确的是( )A、两条不相交的直线叫做平行线 B、在同一平面内,一条直线的平行线有无数条 C、在同一平面内,两条直线一定相交 D、经过一点有且只有一条直线与已 知直线平行9. 如图,在长方形ABCD中,AB=6,BC=10,其内部有边长为a的正方形AEFG与边长为b的正方形HIJK,两个正方形的重合部分也为正方形,且面积为5.若右侧阴影部分的面积S2是左侧阴影部分面积S1的4倍,则正方形AEFG与正方形HIJK的面积之和为( )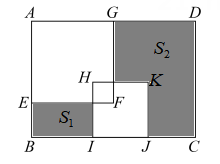 A、20 B、25 C、 D、10. 设 , 为实数,多项式展开后的一次项系数为 , 多项式展开后的一次项系数为:若 , 且 , 均为正整数,则( )A、与的最大值相等,与的最小值也相等 B、与的最大值相等,与的最小值不相等 C、与的最大值不相等,与的最小值相等 D、与的最大值不相等,与的最小值也不相等
A、20 B、25 C、 D、10. 设 , 为实数,多项式展开后的一次项系数为 , 多项式展开后的一次项系数为:若 , 且 , 均为正整数,则( )A、与的最大值相等,与的最小值也相等 B、与的最大值相等,与的最小值不相等 C、与的最大值不相等,与的最小值相等 D、与的最大值不相等,与的最小值也不相等二、填空题(每题3分,共18分)
-
11. 如图是小明学习三线八角时制作的模具,经测量,∠2=100°,要使木条a与b平行,则∠1的度数是°.
 12. 解二元一次方程组时,小华用加减消元法消去未知数y , 按照他的思路,用①+②得到的方程是 .13. 已知m+n=2,mn=-3,则(1+m)(1+n)的值为14. 按照如图所示的程序计算,如开始输入的m值为 , 则最后输出的结果是
12. 解二元一次方程组时,小华用加减消元法消去未知数y , 按照他的思路,用①+②得到的方程是 .13. 已知m+n=2,mn=-3,则(1+m)(1+n)的值为14. 按照如图所示的程序计算,如开始输入的m值为 , 则最后输出的结果是 15. 已知∠A与∠B的两边分别平行,其中∠B=(210-2x)°,则x的值为.16. 图1是一盏可折叠台灯。图2,图3是其平面示意图,固定底座OA⊥OM于点O,支架BA与CB分别可绕点A和B旋转,台灯灯罩可绕点C旋转调节光线角度,台灯最外侧光线CE,CD组成的∠ECD始终保持不变。如图2,调节台灯使光线CD//BA,CE//OM,此时∠BAO=158°,则∠ECD=.现继续调节图2中的支架CB与灯罩,发现当最外侧光线CE与水平方向的夹角∠CQM=29°,且∠ECD的角平分线CP与CB垂直时,光线最适合阅读(如图3),则此时∠ABC=.
15. 已知∠A与∠B的两边分别平行,其中∠B=(210-2x)°,则x的值为.16. 图1是一盏可折叠台灯。图2,图3是其平面示意图,固定底座OA⊥OM于点O,支架BA与CB分别可绕点A和B旋转,台灯灯罩可绕点C旋转调节光线角度,台灯最外侧光线CE,CD组成的∠ECD始终保持不变。如图2,调节台灯使光线CD//BA,CE//OM,此时∠BAO=158°,则∠ECD=.现继续调节图2中的支架CB与灯罩,发现当最外侧光线CE与水平方向的夹角∠CQM=29°,且∠ECD的角平分线CP与CB垂直时,光线最适合阅读(如图3),则此时∠ABC=.
三、解答题(共8题,共72分)
-
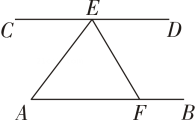
17. 解方程组:(1)、(2)、18. 先化简,再求值: , 其中x=1,y=2.19. 如图,AB∥CD,E是CD上一点,∠AEC=42°,EF平分∠AED交AB于点F,求∠AFE的度数.
 20. 定义新运算“※”:x※y=xy+x2﹣y2 , 化简(2a+3b)※(2a﹣3b),并求出当a=2,b=1时的值.21. 为了纪念革命英雄夏明翰,衡阳市政府计划将一块长为米,宽为米的长方形(如图所示)地块用于宣传革命英雄事迹,规划部门计划将阴影部分进行绿化,中间将修建一座夏明翰雕像.
20. 定义新运算“※”:x※y=xy+x2﹣y2 , 化简(2a+3b)※(2a﹣3b),并求出当a=2,b=1时的值.21. 为了纪念革命英雄夏明翰,衡阳市政府计划将一块长为米,宽为米的长方形(如图所示)地块用于宣传革命英雄事迹,规划部门计划将阴影部分进行绿化,中间将修建一座夏明翰雕像. (1)、试用含a , b的代数式表示绿化的面积是多少平方米?(2)、若 , , 请求出绿化面积.22. 如图, , .
(1)、试用含a , b的代数式表示绿化的面积是多少平方米?(2)、若 , , 请求出绿化面积.22. 如图, , .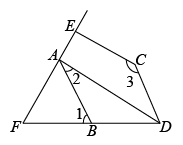 (1)、与平行吗?试说明理由;(2)、若平分 , 于点 , , 求的度数.23. 数学课上,老师用图1中的一张边长为a的正方形纸片A,1张边长为b的正方形纸片B和2张宽与长分别为a与b的长方形纸片C,拼成了如图2所示的大正方形,观察图形并解答下列问题:
(1)、与平行吗?试说明理由;(2)、若平分 , 于点 , , 求的度数.23. 数学课上,老师用图1中的一张边长为a的正方形纸片A,1张边长为b的正方形纸片B和2张宽与长分别为a与b的长方形纸片C,拼成了如图2所示的大正方形,观察图形并解答下列问题: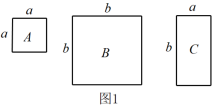
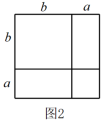
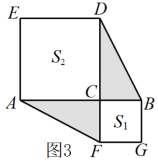 (1)、由图1和图2可以得到的等式为(用含a,b的等式表示);(2)、莉莉想用这三种纸片拼出一个面积为的大长方形,求需A,B,C三种纸片各多少张;(3)、如图3,S1 , S2分别表示边长为p,q的正方形的面积,且A,B,C三点在一条直线上, , . 求图中阴影部分的面积.24.
(1)、由图1和图2可以得到的等式为(用含a,b的等式表示);(2)、莉莉想用这三种纸片拼出一个面积为的大长方形,求需A,B,C三种纸片各多少张;(3)、如图3,S1 , S2分别表示边长为p,q的正方形的面积,且A,B,C三点在一条直线上, , . 求图中阴影部分的面积.24.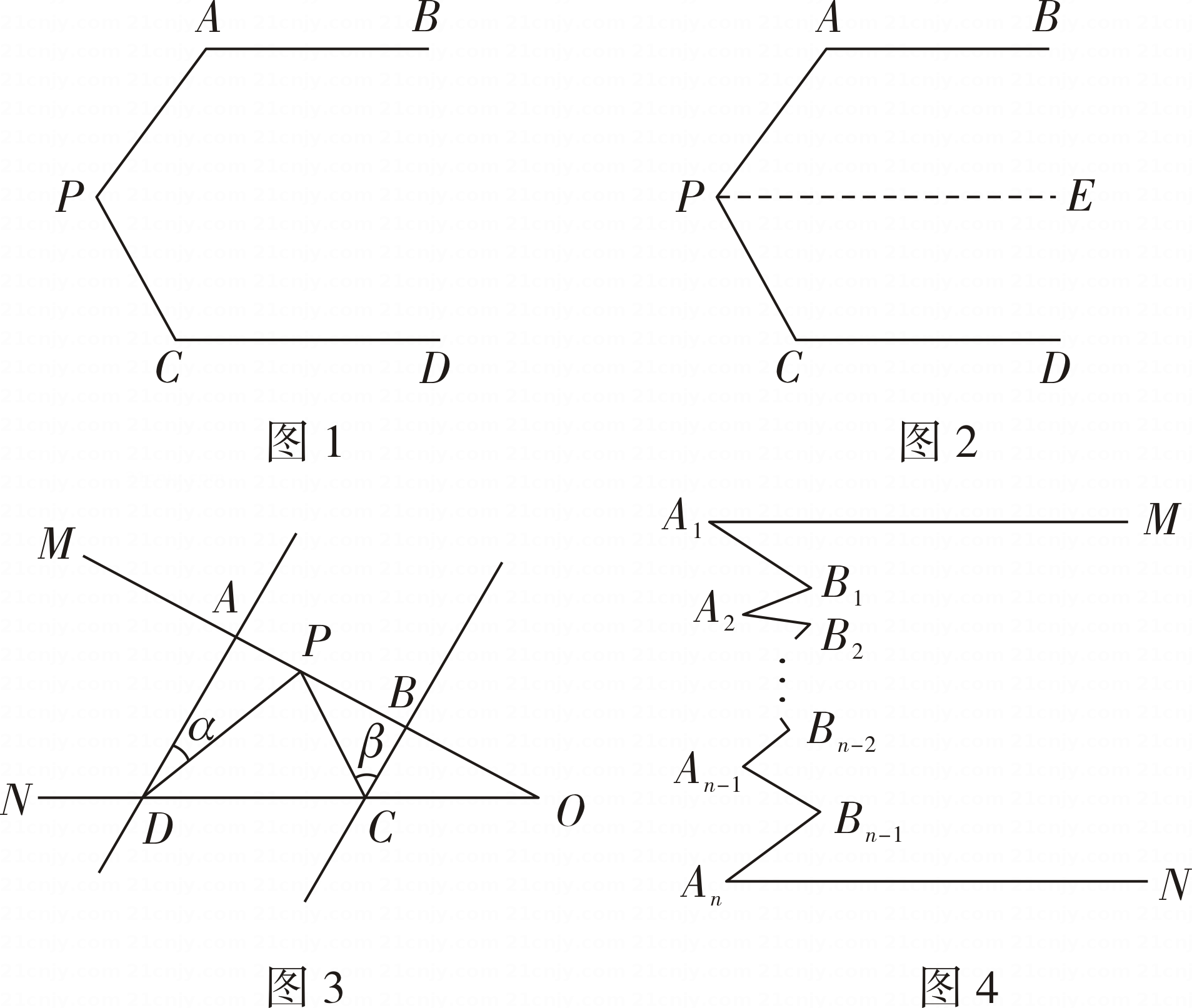 (1)、问题情境:
(1)、问题情境:如图1,已知 AB∥CD,∠APC=108°.求∠PAB+∠PCD的度数.
经过思考,小敏提出思路:如图2,过点 P 作PE∥AB,根据平行线的有关性质,可得∠PAB+∠PCD= °.
(2)、问题迁移:如图3,AD∥BC,点 P 在射线OM 上运动,∠ADP=α,∠BCP=β.
当点 P 在A,B两点之间运动时,∠CPD,α,β之间有何数量关系? 请说明理由.
(3)、当点 P 在A,B 两点外侧运动时(点 P 与点A,B,O不重合),请直接写出∠CPD,α,β之间的数量关系.(4)、问题拓展:如图4, -An是一条折线段.
依据此图信息,把你所发现的结论用数学式子表达出来: