湖北省十堰市茅箭区第一教联体2023-2024学年八年级下学期第一次月考数学试题
试卷更新日期:2024-04-16 类型:月考试卷
一、选择题:本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 要使二次根式有意义,则x的取值范围是( )A、x>8 B、x<8 C、x≤8 D、x≥82. 下列各式计算正确的是( )A、 B、 C、 D、3. 下列各组数中能构成直角三角形的是( )A、4,5,6 B、 , , C、4,5, D、5,12,104. 如图,在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )
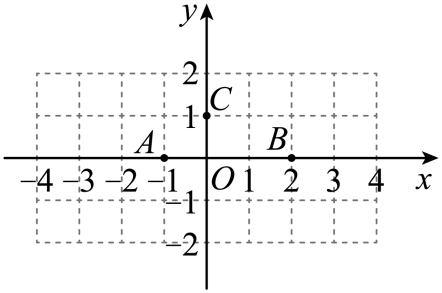 A、(3,1) B、(-4,1) C、(1,-1) D、(-3,1)5. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时, 梯子底端到左墙角的距离BC为0.7m,梯子顶端到地面的距离AC为2.4m.如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离A'D为1.5m,则小巷的宽为( ).
A、(3,1) B、(-4,1) C、(1,-1) D、(-3,1)5. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时, 梯子底端到左墙角的距离BC为0.7m,梯子顶端到地面的距离AC为2.4m.如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离A'D为1.5m,则小巷的宽为( ).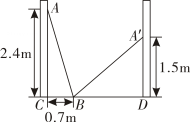 A、2.4m B、2m C、2.5m D、2.7m6. 《九章算术》是我国古代最重要的数学著作之一,它的出现标志着中国古代数学形成了完整的体系.“折竹抵地”问题源自《九章算术》﹔“今有竹高一丈,末折抵地,去本四尺,问折者高几何?”翻译成数学问题是:如图所示, 中, , 尺, 尺,求AC的长.则AC的长为( )
A、2.4m B、2m C、2.5m D、2.7m6. 《九章算术》是我国古代最重要的数学著作之一,它的出现标志着中国古代数学形成了完整的体系.“折竹抵地”问题源自《九章算术》﹔“今有竹高一丈,末折抵地,去本四尺,问折者高几何?”翻译成数学问题是:如图所示, 中, , 尺, 尺,求AC的长.则AC的长为( ) A、4.2尺 B、4.3尺 C、4.4尺 D、4.5尺7. 如图, , 与按如图方式拼接在一起, , , , 则的值为( )
A、4.2尺 B、4.3尺 C、4.4尺 D、4.5尺7. 如图, , 与按如图方式拼接在一起, , , , 则的值为( ) A、 B、 C、 D、8. 如图, 中,对角线 、 相交于点O , 交 于点E , 连接 ,若 的周长为28,则 的周长为( )
A、 B、 C、 D、8. 如图, 中,对角线 、 相交于点O , 交 于点E , 连接 ,若 的周长为28,则 的周长为( )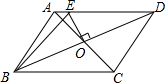 A、28 B、24 C、21 D、149. 阅读下列材料:若一个任意三角形的三边长分别为a , b , c , 记则这个三角形的面积 .古希腊的数学家海伦给出了这个公式的证明,这一公式称为海伦公式.若在海伦公式中, , , , 则( )A、10 B、 C、6 D、10. 在中, , 点D为中点, , 绕点D旋转,分别与边 , 交于E , F两点,下列结论:①;②;③;④始终为等腰直角三角形,其中正确的是( )A、①②④ B、①②③ C、③④ D、①②③④
A、28 B、24 C、21 D、149. 阅读下列材料:若一个任意三角形的三边长分别为a , b , c , 记则这个三角形的面积 .古希腊的数学家海伦给出了这个公式的证明,这一公式称为海伦公式.若在海伦公式中, , , , 则( )A、10 B、 C、6 D、10. 在中, , 点D为中点, , 绕点D旋转,分别与边 , 交于E , F两点,下列结论:①;②;③;④始终为等腰直角三角形,其中正确的是( )A、①②④ B、①②③ C、③④ D、①②③④二、填空题:本题共5小题,每小题3分,共15分.
-
11. 计算: = .12. 当时,代数式的值是 .13. 如图是棱长为4cm的立方体木块,一只蚂蚁现在A点,若在B点处有一块糖,它想尽快吃到这块糖,则蚂蚁沿正方体表面爬行的最短路程是cm .
 14. 如图,在 中,点E在 上,且 平分 ,若 , ,则 的面积为.
14. 如图,在 中,点E在 上,且 平分 ,若 , ,则 的面积为.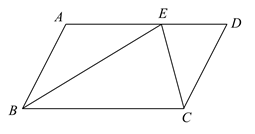 15. 如图, 在中, , , , P是边上一动点, 将沿折叠,点B落在处, 交于D , 则的最大值为 .
15. 如图, 在中, , , , P是边上一动点, 将沿折叠,点B落在处, 交于D , 则的最大值为 .
三、解答题:本题共9小题,共75分.解答应写出文字说明、证明过程或演算步聚.
-
16. 计算:(1)、(2)、17. 先化简,再求值: ÷ ,其中x= +1,y= ﹣1.18. 如图,在四边形 中, , ,垂足分别为点 , .
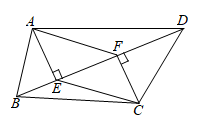 (1)、请你只添加一个条件(不另加辅助线),使得四边形 为平行四边形,你添加的条件是;(2)、添加了条件后,证明四边形 为平行四边形.19. 请运用平行四边形特征按下列要求作图:
(1)、请你只添加一个条件(不另加辅助线),使得四边形 为平行四边形,你添加的条件是;(2)、添加了条件后,证明四边形 为平行四边形.19. 请运用平行四边形特征按下列要求作图: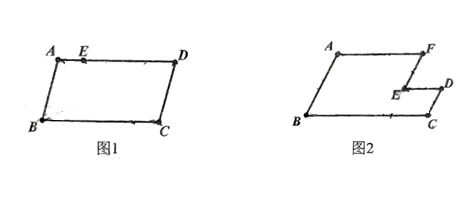 (1)、如图1,中,点E在上, 在上画点F , 使;(2)、如图2, , , 画一条直线平分此多边形的面积.20. 如图,有两只猴子在一棵树高的点B处,它们都要到A处的池塘去喝水,其中一只猴子沿树爬下走到离树处的池塘A处,另一只猴子爬到树顶D后直线跃向池塘的A处,如果两只猴子所经过的路程相等,这棵树高有多少米?树顶D到池塘A的距离有多少米?
(1)、如图1,中,点E在上, 在上画点F , 使;(2)、如图2, , , 画一条直线平分此多边形的面积.20. 如图,有两只猴子在一棵树高的点B处,它们都要到A处的池塘去喝水,其中一只猴子沿树爬下走到离树处的池塘A处,另一只猴子爬到树顶D后直线跃向池塘的A处,如果两只猴子所经过的路程相等,这棵树高有多少米?树顶D到池塘A的距离有多少米? 21. 在平行四边形ABCD中,E,F分别是AB,DC上的点,且AE=CF,连接DE,BF,AF.
21. 在平行四边形ABCD中,E,F分别是AB,DC上的点,且AE=CF,连接DE,BF,AF.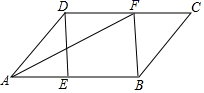 (1)、求证:四边形DEBF是平行四边形;(2)、若AF平分∠DAB,AE=3,DE=4,BE=5,求AF的长.22. 如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线交于点F .
(1)、求证:四边形DEBF是平行四边形;(2)、若AF平分∠DAB,AE=3,DE=4,BE=5,求AF的长.22. 如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线交于点F . (1)、求证:四边形BDFC是平行四边形;(2)、若BC=BD , 求四边形BDFC的面积.23.
(1)、求证:四边形BDFC是平行四边形;(2)、若BC=BD , 求四边形BDFC的面积.23. (1)、问题背景:在中, , , 三边的长分别为 , 求这个三角形的面积.小刚同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点(即三个顶点都在小正方形的顶点处),如图①所示.这样不需求的高,借用网格就能计算出它的面积.
(1)、问题背景:在中, , , 三边的长分别为 , 求这个三角形的面积.小刚同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点(即三个顶点都在小正方形的顶点处),如图①所示.这样不需求的高,借用网格就能计算出它的面积.请你将的面积直接填写在横线上: .
(2)、思维拓展:我们把上述求面积的方法叫作构图法,若中, , , 三边的长分别为 , 请利用图②的正方形网格(每个小正方形的边长为a)画出相应的 , 其中顶点A的位置如图所示.①求出的面积;②直接写出顶点B到的距离(用含a的式子表示).(3)、探索创新:若三边长分别为( , 且),请直接写出这个三角形的面积(用含m , n的式子表示).24. 如图,中, , D为中点,点E在直线上(点E不与点B , C重合),连接 , 过点D作交直线于点F , 连接 . (1)、如图1,当点F与点A重合时,请直接写出线段与的数量关系: .(2)、如图2,当点F不与点A重合时,请写出线段 , , 之间的数量关系,并说明理由;(3)、若 , , , 请直接写出线段AF的长.
(1)、如图1,当点F与点A重合时,请直接写出线段与的数量关系: .(2)、如图2,当点F不与点A重合时,请写出线段 , , 之间的数量关系,并说明理由;(3)、若 , , , 请直接写出线段AF的长.