广西壮族自治区贺州市2024年中考一模数学模拟试题

试卷更新日期：2024-04-16 类型：中考模拟

进入出卷网下载

一、选择题（共12小题，每小题3分，共36分.在每小题给出的四个选项中只有一项是符合要求的，用2B铅笔把答题卡上对应题目的答案标号涂黑）

1. 实数 $- 3$ 的相反数是（）

A、 $- \frac{1}{3}$ B、 $\frac{1}{3}$ C、3 D、 $- 3$

查看试题解析
2. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 $3 a + 2 a = 5 a^{2}$ C、 $a^{6} \div a^{3} = a^{2}$ D、 ${(a^{2})}^{3} = a^{6}$

查看试题解析
4. 不等式 $3 x - 3 > 0$ 的解集是（）

A、 $x < - 1$ B、 $x > - 1$ C、 $x < 1$ D、 $x > 1$

查看试题解析
5. 某段工程施工需要运送土石方总量为 $1 0^{5} m^{3}$ ，设土石方日平均运送量为V（单位： $m^{3}$ /天），完成运送任务所需要的时间为t（单位：天），则V是关于t的（）

A、反比例函数 B、正比例函数 C、一次函数 D、二次函数

查看试题解析
6. 下列长度的三条线段，能组成三角形的是（）

A、5，6，12 B、4，4，8 C、2，3，4 D、2，3，5

查看试题解析
7. 下列二次根式中，化简后能与 $\sqrt{2}$ 进行合并的二次根式是（）

A、 $\sqrt{4}$ B、 $\sqrt{6}$ C、 $\sqrt{8}$ D、 $\sqrt{12}$

查看试题解析
8. 某校准备组织研学活动，需要从青秀山、美丽南方、良风江森林公园、花花大世界四个地点中任选一个前往研学，选中花花大世界的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{3}{4}$

查看试题解析
9. 若点 $A (1 ， 2)$ 向下平移2个单位长度得到对应点 $A^{'}$ ，则点 $A^{'}$ 的坐标是（）

A、 $(- 1 ， 2)$ B、 $(1 ， 0)$ C、 $(1 ， 4)$ D、 $(3 ， 2)$

查看试题解析
10. 如图，在 $△ A B C$ 中，分别以点A和点C为圆心，大于 $\frac{1}{2} A C$ 的长为半径作弧（弧所在圆的半径都相等），两弧相交于M ， N两点，直线 $M N$ 分别与边 $B C$ ， $A C$ 相交于点D ， E ，连接 $A D$ .若 $A C = 8$ ， $A D = 5$ ，则 $D E$ 的长为（）

A、6 B、5 C、4 D、3

查看试题解析
11. 中国高铁的飞速发展，已成为中国现代化建设的重要标志.如图是高铁线路在转向处所设计的圆曲线（即圆弧），高铁列车在转弯时的曲线起点为A ，曲线终点为B ，过点A ， B的两条切线相交于点C ，从A到B行驶的过程中转角 $α$ 为60°，若圆曲线的半径 $O A = 1.5 k m$ ，则圆曲线 $\overset{⌢}{A B}$ 的长为（）

A、 $\frac{π}{4} k m$ B、 $\frac{3 π}{4} k m$ C、 $\frac{π}{2} k m$ D、 $\frac{3 π}{8} k m$

查看试题解析
12. 已知点 $M (6, a - 3)$ ， $N (- 2, a)$ ， $P (2, a)$ 在同一个函数图象上，则这个函数图象可能是（）

A、 B、 C、 D、

查看试题解析

二、填空题（共6小题，每小题2分，共12分.请将答案填在答题卡上）

13. 投篮一次，投进篮筐.这是事件.（填“随机”或“必然”或“不可能”）

查看试题解析
14. 因式分解： $a^{2} - 1$ =.

查看试题解析
15. 如图，在 $▱ A B C D$ 中， $B C = 10$ ， $A C = 8$ ， $B D = 14$ ， $△ A O D$ 的周长是.

查看试题解析
16. 如图，点 $D ， E$ 分别在 $△ A B C$ 的边 $A B ， A C$ 上，且 $D E ∥ B C$ ，点 $F$ 在线段 $B C$ 的延长线上．若 $∠ A D E = 28 °$ ， $∠ A C F = 118 °$ ，则 $∠ A =$ ．

查看试题解析
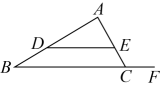17. 如图所示，桔槔是一种原始的汲水工具，它是在一根竖立的架子上加上一根细长的杠杆，末端悬挂一重物，前端悬挂水桶.当人把水桶放入水中打满水以后，由于杠杆末端的重力作用，便能轻易把水提升至所需处，若已知：杠杆 $A B = 6$ 米， $A O : O B = 2 : 1$ ，支架 $O M ⊥ E F$ ， $O M = 3$ 米， $A B$ 可以绕着点O自由旋转，当点A旋转到如图所示位置时 $∠ A O M = 45 °$ ，此时点B到水平地面 $E F$ 的距离为米.（结果保留根号）

查看试题解析
18. 如图，在直角坐标系中， $⊙ A$ 与x轴相切于点B ， $C B$ 为 $⊙ A$ 的直径，点C在函数 $y = \frac{6}{x} (x > 0)$ 的图象上，D为y轴上一点，则 $△ A C D$ 的面积为.

查看试题解析

三、解答题（本大题共8小题，共72分，解答应写出文字说明、证明过程或演算步骤）

19. 计算： $(- 1) \times (- 6) + 2^{2} \div (7 - 5)$ .

查看试题解析
20. 解分式方程： $\frac{2}{x - 3} = \frac{3}{x}$

查看试题解析
21. 如图，小刚在学习了“角平分线上的点到角的两边的距离相等”的性质基础上，进行了更进一步的研究， $O C$ 是 $∠ A O B$ 的角平分线，P是 $O C$ 上一点. $P D ⊥ O A$ 于点D ， $P E ⊥ O B$ 于点E.猜想线段 $O P$ 上任取一点F（O点、P点除外），到垂足D、E的距离也相等，按要求完成：

(1)、线段 $O P$ 上任取一点F（O点、P点除外），连接 $D F$ 、 $E F$ ，请补全图形并标明字母.

(2)、在（1）的基础上，求证： $D F = E F$ .

查看试题解析
22. 2023年9月21日下午，“天宫课堂”第四课在中国空间站开讲，新晋“太空教师”——神舟十六号航天员景海鹏、朱杨柱、桂海潮为广大青少年带来一节精彩的太空科普课.某中学为了解学生对“航空航天知识”的掌握情况，随机抽取50名学生进行测试，并对成绩（百分制）进行整理，信息如下：
a.成绩频数分布表：
成绩x（分） 50≤x＜60 60≤x＜70 70≤x＜80 80≤x＜90 90≤x≤100
频数 7 9 a 16 6
b.成绩在 $70 \leq x < 80$ 这一组的是（单位：分）：70，71，72，72，74，77，78，78，78，79，79，79，根据以上信息，回答下列问题：

(1)、表中a的值为；

(2)、在这次测试中，成绩的中位数是为分，成绩不低于75分的人数占测试人数的百分比为；

(3)、这次测试成绩的平均数是76.4分，甲的测试成绩是80分.乙说：“甲的成绩高于平均数，所以甲的成绩高于一半学生的成绩.”你认为乙的说法正确吗?请说明理由.

查看试题解析
23. 如图，A、P、B、C在圆上， $∠ A P C = ∠ C P B = 60 °$ ，连接 $A B$ 、 $B C$ 、 $A C$ .

(1)、判断 $△ A B C$ 的形状，并证明你的结论；

(2)、若 $∠ P A C = 90 °$ ， $A B = 2 \sqrt{3}$ ，求圆的半径.

查看试题解析

24. 如图，某校的饮水机有温水、开水两个按钮，温水和开水共用一个出水口.温水的温度为30℃，流速为

20 m l / s

；开水的温度为100℃，流速为

15 m l / s

.整个接水的过程不计热量损失.

物理常识：

开水和温水混合时会发生热传递，开水放出的热量等于温水吸收的热量，可以转化为：开水的体积 $\times$ 开水降低的温度 $=$ 温水的体积 $\times$ 温水升高的温度.

(1)、甲同学用空杯先接了6s温水，再接4s开水，接完后杯中共有水

m l

；

(2)、乙同学先接了一会儿温水，又接了一会儿开水，得到一杯

280 m l

温度为40℃的水（不计热损失），求乙同学分别接温水和开水的时间.

查看试题解析

25. 某校计划将新建图书楼的正门设计为一个抛物线型拱门，并要求设计的拱门的跨度与拱高之积为 $48 m^{2}$ ，还要兼顾美观、大方，和谐、通畅等因素，设计部门按要求给出了两个设计方案.现把这两个方案中的拱门图形放入平面直角坐标系中，如图所示：
方案一：抛物线型拱门的跨度 $O N = 12 m$ ，拱高 $P E = 4 m$ .点N在x轴上， $P E ⊥ O N$ ， $O E = E N$ .
方案二：抛物线型拱门的跨度 $O N^{'} = 8 m$ ，拱高 $P^{'} E^{'} = 6 m$ .点 $N^{'}$ 在x轴上， $P^{'} E^{'} ⊥ O N^{'}$ ， $O E^{'} = E^{'} N^{'}$ .要在拱门中设置高为 $3 m$ 的矩形框架，其面积越大越好（框架的粗细忽略不计）.方案一中，矩形框架 $A B C D$ 的面积记为 $S_{1}$ ，点A、D在抛物线上，边 $B C$ 在 $O N$ 上；方案二中，矩形框架 $A^{'} B^{'} C^{'} D^{'}$ 的面积记为 $S_{2}$ ，点 $A^{'}$ ， $D^{'}$ 在抛物线上，边 $B^{'} C^{'}$ 在 $O N^{'}$ 上.现知，小华已正确求出方案一中，当 $A B = 3 m$ 时， $S_{1} = 18 m^{2}$ ，请你根据以上提供的相关信息，解答下列问题：

(1)、求方案二中抛物线的函数表达式；

(2)、在方案二中，当 $A^{'} B^{'} = 3 m$ 时，求矩形框架 $A^{'} B^{'} C^{'} D^{'}$ 的面积 $S_{2}$ 并比较 $S_{1}$ ， $S_{2}$ 的大小.

查看试题解析
26.
图① 图② 备用图

(1)、【特例探究】如图①，正方形 $A B C D$ 的对角线相交于点O ，点O又是正方形 $A_{1} B_{1} C_{1} O$ 的一个顶点，而且这两个正方形的边长相等.无论正方形 $A_{1} B_{1} C_{1} O$ 绕点O怎样转动，两个正方形重叠部分的面积总等于一个正方形面积的，说明理由.

(2)、【类比迁移】如图②，正方形 $A B C D$ 的对角线 $A C$ 上一点P ， $∠ E P F = 90 °$ ，且 $P A : P C = k$ .
①判断 $P E$ 与 $P F$ 的数量关系（用含k的式子表示），并说明理由；
②若 $k = \frac{1}{2}$ ， $A C = 24$ ，当点F与点B重合时，求 $A E$ 的长.

查看试题解析

成绩x（分）	50≤x＜60	60≤x＜70	70≤x＜80	80≤x＜90	90≤x≤100
频数	7	9	a	16	6