广东省深圳市蛇口育才教育集团2024年中考一模数学试题
试卷更新日期:2024-04-16 类型:中考模拟
一、选择题(本题有10小题,每题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确的选项用2B铅笔填涂在答题卡上)
-
1. 实数在数轴上对应的点如图所示,下列各数中比实数小的是( )
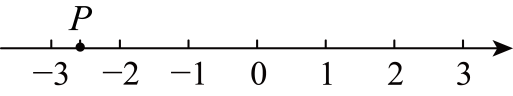 A、 B、 C、 D、2. 积木有助于开发智力,有利于数学概念的早期培养.某积木配件如图所示,则它的左视图为( )
A、 B、 C、 D、2. 积木有助于开发智力,有利于数学概念的早期培养.某积木配件如图所示,则它的左视图为( )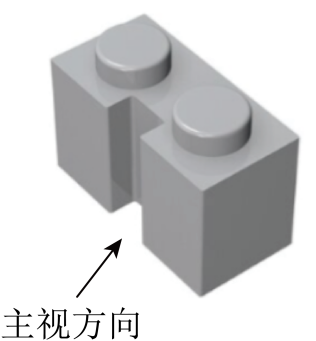 A、
A、 B、
B、 C、
C、 D、
D、 3. 人才是深圳城市发展的重要基因,深圳人才公园是全国第一个人才主题公园,占地面积约平方米.数据用科学记数法表示为( )A、 B、 C、 D、4. 在项目化学习中,“水是生命之源”项目组为了解本地区人均淡水消耗量,需要从四名同学(两名男生,两名女生)中随机抽取两人,组成调查小组进行社会调查,恰好抽到一名男生和一名女生的概率是( )A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心的光线相交于点 , 点为焦点.若 , 则的度数为( )
3. 人才是深圳城市发展的重要基因,深圳人才公园是全国第一个人才主题公园,占地面积约平方米.数据用科学记数法表示为( )A、 B、 C、 D、4. 在项目化学习中,“水是生命之源”项目组为了解本地区人均淡水消耗量,需要从四名同学(两名男生,两名女生)中随机抽取两人,组成调查小组进行社会调查,恰好抽到一名男生和一名女生的概率是( )A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心的光线相交于点 , 点为焦点.若 , 则的度数为( )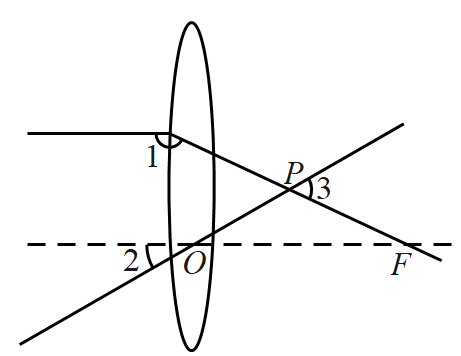 A、 B、 C、 D、7. 榫卯是古代中国建筑、家具及其他器械的主要结构方式.如图,在某燕尾榫中,榫槽的横截面是梯形,其中 , , 燕尾角 , 外口宽 , 榫槽深度是 , 则它的里口宽为( )
A、 B、 C、 D、7. 榫卯是古代中国建筑、家具及其他器械的主要结构方式.如图,在某燕尾榫中,榫槽的横截面是梯形,其中 , , 燕尾角 , 外口宽 , 榫槽深度是 , 则它的里口宽为( )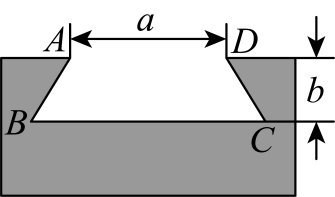 A、 B、 C、 D、8. 明代《算法纂要》书中有一题:“牧童分杏各争竞,不知人数不知杏.三人五个多十枚,四人八枚两个剩.问有几个牧童几个杏?”题目大意是:牧童们要分一堆杏,不知道人数也不知道有多少个杏.若人一组,每组个杏,则多个杏.若人一组,每组个杏,则多个杏.有多少个牧童,多少个杏?设共有个牧童,则下列方程正确的是( )A、 B、 C、 D、9. 如图,矩形中, , , 点在边上,连接 , . 将线段绕点逆时针旋转 , 点的对应点为点 , 连接 , 则的值为( )
A、 B、 C、 D、8. 明代《算法纂要》书中有一题:“牧童分杏各争竞,不知人数不知杏.三人五个多十枚,四人八枚两个剩.问有几个牧童几个杏?”题目大意是:牧童们要分一堆杏,不知道人数也不知道有多少个杏.若人一组,每组个杏,则多个杏.若人一组,每组个杏,则多个杏.有多少个牧童,多少个杏?设共有个牧童,则下列方程正确的是( )A、 B、 C、 D、9. 如图,矩形中, , , 点在边上,连接 , . 将线段绕点逆时针旋转 , 点的对应点为点 , 连接 , 则的值为( )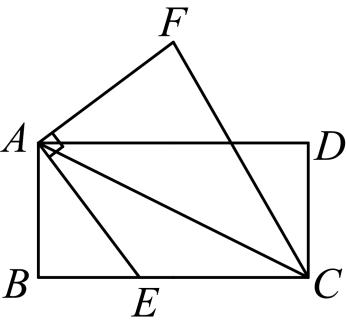 A、 B、 C、 D、10. 已知二次函数经过点、和 , 若在 , , 这三个实数中,只有一个是正数,则的取值范围为( )A、 B、 C、 D、
A、 B、 C、 D、10. 已知二次函数经过点、和 , 若在 , , 这三个实数中,只有一个是正数,则的取值范围为( )A、 B、 C、 D、二、填空题(本题有5小题,每题3分,共15分,把答案填在答题卡上)
-
11. 因式分解 = .12. “每天一节体育课”成深圳中小学生标配.某校九年级三班随机抽取了名男生进行引体向上测试,他们的成绩(单位:个)如下: . 则这组数据的中位数为 .13. 如图所示的网格中,每个小正方形的边长均为1,点A , B , C均在小正方形的顶点上,且点D在上, , 则的长为 .
 14. 如图,在平面直角坐标系中,等腰的底边在轴的正半轴上,顶点在反比例函数的图像上,延长交轴于点 , 若 , 的面积为 , 则的值为 .
14. 如图,在平面直角坐标系中,等腰的底边在轴的正半轴上,顶点在反比例函数的图像上,延长交轴于点 , 若 , 的面积为 , 则的值为 . 15. 如图,在正方形的对角线上取一点 , 使得 , 连接 , 将沿翻折得到 , 连接 . 若 , 则的长为 .
15. 如图,在正方形的对角线上取一点 , 使得 , 连接 , 将沿翻折得到 , 连接 . 若 , 则的长为 .
三、解答题(本题共7小题,共55分)
-
16. 计算: .17. 先化简 , 再从不等式组中选择一个适当的整数,代入求值.18. 科学教育是提升国家科技竞争力、培养创新人才、提高全民科学素质的重要基础。某学校计划在八年级开设“人工智能”“无人机”“创客”“航模”四门校本课程,要求每人必须参加,并且只能选择其中一门课程,为了解学生对这四门课程的选择情况,学校从八年级全体学生中随机抽取部分学生进行问卷调查,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(部分信息未给出).

请你根据以上信息解决下列问题:
(1)、参加问卷调查的学生人数为名,补全条形统计图(画图并标注相应数据);(2)、在扇形统计图中,选择“创客”课程的学生占 , 所对应的圆心角度数为;(3)、若该校八年级一共有名学生,试估计选择“航模”课程的学生有多少名?19. 某社区采购春节慰问礼品,购买了甲、乙两种类型的粮油套装.甲种粮油套装单价比乙种粮油套装单价多元,用元购买甲种粮油套装和用元购买乙种粮油套装的数量相同.(1)、求甲、乙两种粮油套装的单价分别是多少元?(2)、社区准备再次购买甲种和乙种粮油套装共件,购买乙种粮油套装不超过甲种粮油套装的倍,且商家给出了两种粮油套装均打八折的优惠.问购买甲种和乙种粮油套装各多少件时花费最少?最少花费是多少元?20. 如图,在中,以为直径作交、于点、 , 过点作于点 , 交的延长线于点 . (1)、下列条件:
(1)、下列条件:①是边的中点;
②是的中点;
③ .
请从中选择一个能证明直线是的切线的条件,并写出证明过程;
(2)、若直线是的切线,且 , , 求的长.21. 科研人员为了研究弹射器的某项性能,利用无人机测量小钢球竖直向上运动的相关数据.在地面用弹射器(高度不计)竖直向上弹射一个小钢球(忽略空气阻力),科研人员测量出小钢球离地面高度(米)与其运动时间(秒)的几组数据如下表:运动时间(秒)
离地面高度(米)
 (1)、在上图平面直角坐标系中,描出上表中各组对应值为坐标的点,并用平滑的曲线连接:科研人员发现,小钢球离地面高度(米)与其运动时间(秒)成二次函数关系,请求出关于的函数关系式(不要求写出自变量的取值范围).(2)、在弹射小钢球的同一时刻,无人机开始保持匀速竖直上升,无人机离地面高度(米)与小钢球运动时间(秒)之间的函数关系式为 .
(1)、在上图平面直角坐标系中,描出上表中各组对应值为坐标的点,并用平滑的曲线连接:科研人员发现,小钢球离地面高度(米)与其运动时间(秒)成二次函数关系,请求出关于的函数关系式(不要求写出自变量的取值范围).(2)、在弹射小钢球的同一时刻,无人机开始保持匀速竖直上升,无人机离地面高度(米)与小钢球运动时间(秒)之间的函数关系式为 .在小钢球运动过程中,当无人机高度不大于小钢球高度时,无人机可以采集到某项相关性能数据,则能采集到该性能数据的时长为_▲_秒;
弹射器间隔秒弹射第二枚小钢球,其飞行路径视为同一条抛物线.当两枚小钢球处于同一高度时,求此时无人机离地面的高度.
22. 如图1,菱形中, , , 是边上一动点(不与点重合),连接 , 点关于直线的对称点为 , 连接并延长交直线于点是的中点,连接 . (1)、填空: , (用含的代数式表示);(2)、如图2,当 , 题干中其余条件均不变,连接 . 求证: .(3)、(2)的条件下,连接 .
(1)、填空: , (用含的代数式表示);(2)、如图2,当 , 题干中其余条件均不变,连接 . 求证: .(3)、(2)的条件下,连接 .①若动点运动到边的中点处时,的面积为 .
②在动点的整个运动过程中,面积的最大值为 .