浙江省金华市+义乌市北苑六校联考2023-2024学年七年级下学期3月月考数学试题
试卷更新日期:2024-04-16 类型:月考试卷
一、选择题(本大题共10小题,每小题3分,共30分.)
-
1. 下面四个选项中的图形,可以从所给的心形图平移得到的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 若是关于y的二元一次方程的一组解,则a的值为( )A、1 B、2 C、3 D、43. 下列图形中,与不是同位角的是( )A、
2. 若是关于y的二元一次方程的一组解,则a的值为( )A、1 B、2 C、3 D、43. 下列图形中,与不是同位角的是( )A、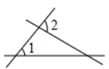 B、
B、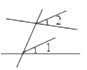 C、
C、 D、
D、 4. 若方程是关于x , y的二元一次方程,则a的值为( )A、 B、 C、0 D、15. 下面的计算,不正确的是( )A、 B、 C、 D、6. 如图,将直角三角形的直角顶点放在直尺的一边BC上(),若 , 则的度数为( )
4. 若方程是关于x , y的二元一次方程,则a的值为( )A、 B、 C、0 D、15. 下面的计算,不正确的是( )A、 B、 C、 D、6. 如图,将直角三角形的直角顶点放在直尺的一边BC上(),若 , 则的度数为( ) A、 B、 C、 D、7. 现代办公纸张通常以A0,A1,A2,A3,A4等标记来衣示纸张的幅面规格,一张A2纸可裁成2张A3纸或4张A4纸.现计划将100张A2纸裁成A3纸和A4纸,两者共计300张,设可裁成A3纸x张,A4纸y张,根据题意,可列方程组( )A、 B、 C、 D、8. 在长方形ABCD中放入六个长、宽都相同的小长方形,所标尺寸如图所示,则图中阴影部分的面积之和为( )
A、 B、 C、 D、7. 现代办公纸张通常以A0,A1,A2,A3,A4等标记来衣示纸张的幅面规格,一张A2纸可裁成2张A3纸或4张A4纸.现计划将100张A2纸裁成A3纸和A4纸,两者共计300张,设可裁成A3纸x张,A4纸y张,根据题意,可列方程组( )A、 B、 C、 D、8. 在长方形ABCD中放入六个长、宽都相同的小长方形,所标尺寸如图所示,则图中阴影部分的面积之和为( ) A、48 B、44 C、36 D、249. 如图, , 那么( )
A、48 B、44 C、36 D、249. 如图, , 那么( ) A、 B、 C、 D、10. 已知关于 , 的方程组给出下列结论:
A、 B、 C、 D、10. 已知关于 , 的方程组给出下列结论:①当时,方程组的解也是的解;
②无论取何值 , 的值不可能是互为相反数;
③ , 都为自然数的解有对;
④若 , 则 .
正确的有几个( )
A、 B、 C、 D、二、填空题(本大题共6小题,每小题3分,共18分)
-
11. 把方程变形,用含x的代数式表示y , 则 .12. 如图,已知 , 则的度数为 .
 13. 计算: .14. 已知a , b满足 , 则 .15. 已知方程组的解是 , 则方程组的解是 .16. 有长方形纸片ABCD , E , F分别是AD , BC上一点,().将纸片沿EF折叠成图1(C , D的对应点分别为 , ),再沿GF折叠成图2( , 的对应点分别为N , M).
13. 计算: .14. 已知a , b满足 , 则 .15. 已知方程组的解是 , 则方程组的解是 .16. 有长方形纸片ABCD , E , F分别是AD , BC上一点,().将纸片沿EF折叠成图1(C , D的对应点分别为 , ),再沿GF折叠成图2( , 的对应点分别为N , M). (1)、如图1,当时,度.(2)、如图2,若GP平分交直线EF于点P , 则(用含x的式子表示)
(1)、如图1,当时,度.(2)、如图2,若GP平分交直线EF于点P , 则(用含x的式子表示)三、解答题(本大题共8小题,第17-22每题6分,第23,24每题8分,共52分。)
-
17. 解方程组:(1)、(2)、18. 先化简,再求值: , 其中 .19. 如图, , 点E是直线AB上的一点,CE平分 .
 (1)、求的度数;(2)、若 , 求证: .20.(1)、若 , 求代数式的值.(2)、已知: , 求的值.21. 如图,在直角三角形ABC中, , , 沿AB方向平移至 , 若 .
(1)、求的度数;(2)、若 , 求证: .20.(1)、若 , 求代数式的值.(2)、已知: , 求的值.21. 如图,在直角三角形ABC中, , , 沿AB方向平移至 , 若 . (1)、求沿AB方向平移的距离;(2)、求四边形AEFC的周长.22. 阅读下列解方程组的方法,然后解答问题:
(1)、求沿AB方向平移的距离;(2)、求四边形AEFC的周长.22. 阅读下列解方程组的方法,然后解答问题:解方程组时,由于x、y的系数及常数项的数值较大,如果用常规的代入消元法、加减消元法来解,那将是计算量大,且易出现运算错误,而采用下面的解法则比较简单:
②-①得: , 所以③
③×14得:④
①-④得: , 从而得
所以原方程组的解是
(1)、请你运用上述方法解方程组(2)、请你直接写出方程组的解是;(3)、猜测关于x、y的方程组的解是什么?并用方程组的解加以验证.23. 水果商贩小王到水果批发市场进货,他了解到草莓的批发价格是每箱60元,苹果的批发价格是每箱40元.小王购得草莓和苹果共60箱,刚好花费3100元.(1)、问草莓、苹果各购买了多少箱?(2)、小王有甲、乙两家店铺,每售出一箱草莓和苹果,甲店分别获利15元和20元,乙店分别获利12元和16元.设老徐将购进的60箱水果分配给甲店草莓a箱,苹果b箱,其余均分配给乙店.由于他口碑良好,两家店都很快卖完了这批水果.①若小王在甲店获利600元,则他在乙店获利多少元?
②若小王希望获得总利润为1000元,则__▲_.(直接写出答案)
24. 义乌江滨绿廊分布于义乌江两岸,东起阳光大道,南至环城路,全长约14千米,总面积400多万平方米,是市民散步休闲的好去处.为了安全起见计划在某段江两岸安置了两座可旋转探照灯.如图1所示灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒3度,灯B转动的速度是每秒2度,假定江两岸是平行的,即 , 且 . (1)、填空:;(2)、若灯B射线先转动10秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?(3)、如图2,若两灯同时开始转动,两灯射出的光束交于点C , 则在灯B射线到达BQ之前,A灯转动秒时, . (在横线处直接写出答案)
(1)、填空:;(2)、若灯B射线先转动10秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?(3)、如图2,若两灯同时开始转动,两灯射出的光束交于点C , 则在灯B射线到达BQ之前,A灯转动秒时, . (在横线处直接写出答案)