浙江省G3联盟2024年中考数学第二次联考试卷

试卷更新日期：2024-04-16 类型：中考模拟

进入出卷网下载

一、选择题：本题共10小题，每小题3分，共30分。在每小题给出的选项中，只有一项是符合题目要求的。

1. 这是 $2024$ 年 $1$ 月某日的气温实施预测情况，则通过预测图可知，下午 $5$ 时的气温和此时气温的相对差值为（）

A、 $4 ℃$ B、 $3 ℃$ C、 $2 ℃$ D、 $- 4 ℃$

查看试题解析
2. “天有日月，道分阴阳”，从古至今，中国人一直都在追求对称美 $.$ 中国传统图形比较注重于对称，其集中体现在文字和建筑、绘画上，下列图形、文字为轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. $2023$ 年杭州亚运会，有五位同学将参加“中国舞迎亚运”活动，已知小队中的每个人的身高 $($ 单位： $c m)$ 分别为： $168$ 、 $167$ 、 $170$ 、 $172$ 、 $158 .$ 则这些队员的身高的方差为（）

A、 $116$ B、 $33.4$ C、 $23.2$ D、 $4.8$

查看试题解析
4. 某商场举办促销活动，负责人在一个不透明的袋子里装着 $8$ 个大小、质量相同的小球，其中 $5$ 个为红色、 $2$ 个为黄色、 $1$ 个为绿色，若要获奖需要一次性摸出 $2$ 个红球和 $1$ 个黄球，那么获奖的概率为（）

A、 $\frac{25}{256}$ B、 $\frac{3}{8}$ C、 $\frac{1}{4}$ D、 $\frac{5}{14}$

查看试题解析
5. 如图，在 $R t △ A B C$ 中， $D$ 为 $B C$ 的中点，若 $A D = \sqrt{2} C D$ ， $A B = B D$ ，则 $t a n ∠ C$ 的值为（）

A、 $\sqrt{2}$ B、 $2$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{1}{2}$

查看试题解析
6. 如图，在 $⊙ A$ 上有 $C$ 、 $E$ 、 $F$ 、 $G$ 四个点，其中 $C G$ 为 $∠ A C E$ 的角平分线，若 $∠ A = 120 °$ ， $E$ 、 $A$ 、 $F$ 共线，则 $∠ G C F$ 的度数为（）

A、 $75 °$ B、 $60 °$ C、 $45 °$ D、 $90 °$

查看试题解析
7. 如图，四个边长均为 $1$ 的正方形如图摆放，其中三个顶点位于坐标轴上，其中一个顶点在反比例函数 $y = \frac{k}{x}$ 的图象上，则 $k$ 的值为（）

A、 $5$ B、 $6$ C、 $7$ D、 $8$

查看试题解析
8. 在平面直角坐标系中，一次函数 $y_{1} = m (x + 1) + 1 (m \neq 0)$ 和 $y_{2} = a (x - 1) + 2 (a \neq 0)$ ，无论 $x$ 取何值，始终有 $y_{2} < y_{1}$ ，则 $m$ 的取值为（）

A、 $m \neq 0$ B、 $m > \frac{1}{2}$ C、 $m < \frac{1}{2}$ D、 $m < \frac{1}{2}$ 且 $m \neq 0$

查看试题解析
9. 点 $A (- 2, m)$ ， $B (4, n)$ 都在二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象上，若 $m > n$ ，则下列可能成立的是（）

A、当 $a < 0$ 时， $4 a + b = 0$ B、当 $a < 0$ 时， $2 a + b = 0$ C、当 $a > 0$ 时， $3 a + b = 0$ D、当 $a > 0$ 时， $a + b = 0$

查看试题解析
10. 将两张全等的等腰直角三角形纸片 $△ A B H$ 与 $△ C D F$ 和一张正方形纸片 $E F G H$ 按照如图所示的方式拼成一个平行四边形 $A B C D$ ，同时形成了剩余部分 $($ 即 $△ B E F$ ， $△ B F C$ ， $△ A H D$ ， $△ H D G)$ ，若只知道阴影部分的面积，则不能直接求出（）

A、 $△ B E F$ 的面积 B、 $△ C D F$ 的面积 C、平行四边形 $A B C D$ 的面积 D、剩余部分的面积之和与正方形 $E F G H$ 面积和

查看试题解析

二、填空题：本题共6小题，每小题4分，共24分。

11. 定义一种运算 $∣\begin{matrix} a & b \\ c & d \end{matrix}∣ = a d - b c$ ，计算 $∣\begin{matrix} \sqrt{5} & s i n 60 ° \\ 2 & \sqrt{15} \end{matrix}∣ =$ ．

查看试题解析
12. 从如图的一块半径为 $1 m$ 的铁圆盘上剪出一个圆周角为 $120 °$ 扇形 $A B C$ ，若将剪下的扇形围成一个圆锥，则该圆锥的体积为．

查看试题解析
13. 某校区的输水管模型如图，输水管的直径为 $4 m$ ，某时刻水面 $A B$ 满足 $∠ A O B = 60 °$ ，则此时水管截面的水面面积 $($ 即阴影部分面积 $)$ 为．

查看试题解析
14. 平面直角坐标系 $x O y$ 中，直线 $y = \frac{1}{2} (x + 3)$ 分别与函数 $y = \frac{k}{x} (k > 0)$ 的图象交于 $A$ 、 $B$ ，若 $y$ 轴负半轴上存在点 $C$ 使得 $△ A B C$ 是以 $C$ 为直角顶点的等腰直角三角形，则 $k$ 为．

查看试题解析
15. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，以点 $B$ 为圆心、 $B A$ 为半径画劣弧 $\overset{⏜}{A D}$ 交射线 $C B$ 于点 $D$ ， $M$ 为 $\overset{⏜}{A D}$ 的中点，联结 $C M$ 、 $A D$ ， $C M$ 分别交 $A B$ 、 $A D$ 于点 $E$ 、 $F$ ，如果点 $B$ 是线段 $C D$ 的黄金分割点，则 $c o s ∠ A B C =$ ．

查看试题解析
16. 在抛物线 $y = \frac{1}{4} x^{2}$ 上，过 $y$ 轴上点 $E$ 作两条相互垂直的直线与抛物线分别交于 $A$ ， $B$ ， $C$ ， $D$ ，且 $M$ ， $N$ 分别是线段 $A B$ ， $C D$ 的中点， $△ E M N$ 面积的最小值为．

查看试题解析

三、解答题：本题共7小题，共66分。解答应写出文字说明，证明过程或演算步骤。

17. 如图，已知 $A B$ 是 $⊙ O$ 的直径，弦 $C D ⊥ A B$ 于点 $E$ ， $G$ 是 $\overset{⏜}{A D}$ 上一点， $A G$ 、 $C D$ 的延长线相交于点 $F$ ，求证： $∠ F G D = ∠ A G C$ ．

查看试题解析
18. 图 $1$ ，图 $2$ 都是由边长为 $1$ 的小等边三角形构成的网格，每个小等边三角形的顶点称为格点，线段 $A B$ 的端点在格点上，分别按要求画出图形：

(1)、在图 $1$ 中画出两个以 $A B$ 为斜边的直角三角形 $A B C$ ，且点 $C$ 在格点上；

(2)、在图 $2$ 中画出一个以 $A B$ 为对角线的菱形 $A D B E$ ，且 $D$ ， $E$ 在格点上．

查看试题解析
19. 法国著名的思想家伏尔泰说过“生命在于运动”，某大学小组为了调查初中同学学生课后运动时间，按照时间分为 $A$ 、 $B$ 、 $C$ 、 $D$ 四个等级，绘制了如下不完整统计表：

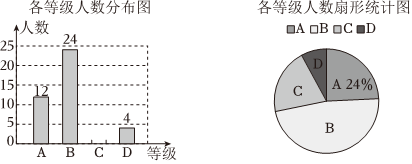(1)、求本次调查的总人数，并且补全人数分布图；

(2)、估计本次调查的中位数位于 $A$ 、 $B$ 、 $C$ 、 $D$ 哪个等级中；

(3)、小宁认为我们可以根据本次调查数据精确预测全市初中生为 $A$ 等的人数，请判断他这句话的正误，并说明理由．

查看试题解析
20. 顶点为 $D$ 的二次函数 $y = a x^{2} + b x + c (a < 0)$ 满足以下三个条件的任意两个：
$①$ 其与 $y$ 轴的交点为 $(0,1)$ ；
$②$ 其与 $x$ 轴的交点为 $(- 1,0)$ 和 $(3,0)$ ；
$③$ 该函数其最大值为 $12$ ．

(1)、从以上条件任选两个，求出函数的表达式；

(2)、若存在直线 $y = - 1$ ，二次函数上的存在一个点 $A$ ，使得 $A D$ 等于 $A$ 到直线的距离，求出 $A$ 点的坐标．

查看试题解析

21.

教学实践活动： $910$ 班测量雷峰塔高度实践的相关数据
活动 $1$	如图， $A$ 点为塔顶，将 $-$ 根木棒立在 $D$ 处， $A C$ 的连线交地面于 $Q$ 点，同理将相同长度的木棒立在 $F$ 处，同时得到 $P$ 点 $.$ 若移动木棒使得 $C D = Q D$ ，在 $E$ 点的仰角为 $30 °$ ，则 $∠ P A Q =$ ▲ ．
活动 $2$	如图，小组 $2$ 设计了此测量方法，若 $C D$ 的长度为 $18 m$ ，已知 $∠ α = 37 °$ ， $∠ β = 30 °$ ，则可以得到塔的高度大约为 ▲ $. ($ 参考数据： $\sqrt{3} \approx 1.732$ ， $s i n 37 ° \approx 0.602$ ， $c o s 37 ° \approx 0.799$ ， $t a n 37 ° \approx 0.754)$
总结与取优
老师做了一个小小的总结，并且设计了一个新的方案，已知塔前有一高 $4$ 米的小树 $C D$ ，发现水平地面上点 $E$ 、树顶和塔顶 $A$ 恰好在一条直线上，测得 $B D = 57$ 米， $D$ 、 $E$ 之间有一个花圃无法测量，然后在 $E$ 处放置一个平面镜，沿 $B E$ 后退，退到 $G$ 处恰好在平面中看到树顶 $C$ 的像，此时 $E G = 2.4$ 米，测量者眼睛到地面的距离 $F G$ 为 $1.6$ 米，求出塔高 $A B$ ．

查看试题解析

22. 在平面直角坐标系 $x O y$ 中，抛物线 $y = a x^{2} + b x + c (a, b, c$ 为常数，且 $a \neq 0)$ 经过 $A (- 2, - 4)$ 和 $B (3,1)$ 两点．

(1)、求 $b$ 和 $c$ 的值 $($ 用含 $a$ 的代数式表示 $)$ ；

(2)、若该抛物线开口向下，且经过 $C (2 m - 3, n)$ ， $D (7 - 2 m, n)$ 两点，当 $k - 3 < x < k + 3$ 时， $y$ 随 $x$ 的增大而减小，求 $k$ 的取值范围；

(3)、已知点 $M (- 6,5)$ ， $N (2,5)$ ，若该抛物线与线段 $M N$ 恰有一个公共点时，结合函数图象，求 $a$ 的取值范围．

查看试题解析
23. 如图，四边形 $A B C D$ 内接于 $⊙ O$ ， $A C$ 为 $⊙ O$ 的直径， $D E ⊥ A C$ 于点 $F$ 交 $B C$ 于点 $E$ ．

(1)、设 $∠ D B C = α$ ，试用含 $α$ 的代数式表示 $∠ A D E$ ；

(2)、如图 $2$ ，若 $B E = 3 C E$ ，求 $\frac{B D}{D E}$ 的值；

(3)、在 $(2)$ 的条件下，若 $A C$ ， $B D$ 交于点 $G$ ，设 $\frac{F G}{C F} = x$ ， $c o s ∠ B D E = y$ ．
$①$ 求 $y$ 关于 $x$ 的函数表达式；
$②$ 若 $B C = B D$ ，求 $y$ 的值．

查看试题解析