湖北省襄阳市襄州区2023-2024学年七年级下学期月考数学试题

试卷更新日期：2024-04-16 类型：月考试卷

进入出卷网下载

一、选择题（共10小题，每小题3分，满分30分）

1. 下列各选项， $∠ 1$ 和 $∠ 2$ 互为邻补角的是（）

A、 B、 C、 D、

查看试题解析
2. 下列选项是无理数的为（）

A、 $- \frac{22}{13}$ B、 $\sqrt{4}$ C、 $3.1415926$ D、 $π$

查看试题解析
3. 如图，给出了过直线外一点作已知直线的平行线的方法，其依据是（）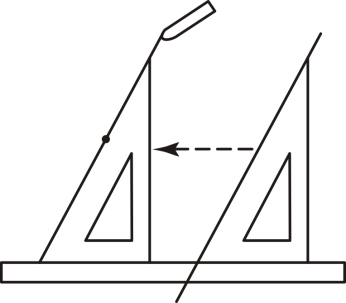

A、同位角相等，两直线平行 B、内错角相等，两直线平行 C、两直线平行，同位角相等 D、两直线平行，内错角相等

查看试题解析
4. 如图，点 $E$ 在 $C D$ 的延长线上，下列条件中不能判定 $A B ∥ C D$ 的是（）

A、 $∠ B + ∠ B D C = 180 °$ B、 $∠ 3 = ∠ 4$ C、 $∠ 5 = ∠ B$ D、 $∠ 1 = ∠ 2$

查看试题解析
5. 下列各式正确的是（）

A、 $\sqrt{16} = \pm 4$ B、 $\sqrt[3]{- 64} = - 8$ C、 $\sqrt{{(- 3)}^{2}} = 3$ D、 $\sqrt{2^{2}} = - 2$

查看试题解析
6. 如图，已知 $∠ 1 = 60 °$ ， $∠ 2 = 60 °$ ， $∠ 3 = 68 °$ ，则 $∠ 4$ 等于（）

A、 $68 °$ B、 $60 °$ C、 $102 °$ D、 $112 °$

查看试题解析
7. 下列说法：①对顶角相等；②在同一平面内，垂直于同一条直线的两直线平行；③相等的角是对顶角；④内错角相等．其中错误的有(　　)

A、①② B、①③ C、②④ D、③④

查看试题解析
8. 下列四组角中是内错角的是（）

A、 $∠ 1$ 与 $∠ 2$ B、 $∠ 1$ 与 $∠ 3$ C、 $∠ 1$ 与 $∠ 4$ D、 $∠ 2$ 与 $∠ 4$

查看试题解析
9. 如图，直线 $A B$ 、 $C D$ 相交于点O ， $∠ D O F = 90 °$ ， $O F$ 平分 $∠ A O E$ ，若 $∠ B O D = 33 °$ ，则 $∠ E O F$ 的度数为（）．

A、64° B、57° C、48° D、33°

查看试题解析
10. 如图1的晾衣架中存在多组平行关系，将晾衣架的侧面抽象成如图2的数学问题，已知 $A B ∥ M N ∥ P Q$ ，若 $∠ 2 = 100 °$ ， $∠ 3 = 130 °$ ，则 $∠ 1$ 的度数为（）

A、 $40 °$ B、 $50 °$ C、 $60 °$ D、 $70 °$

查看试题解析

二、填空题（共6小题，每小题3分，满分18分）

11. 49的算术平方根是， $\sqrt[3]{64}$ 的平方根为， $- \sqrt{6}$ 的相反数是．

查看试题解析
12. 将命题“同角的补角相等”改写成“如果……那么……”的形式为

查看试题解析
13. 已知 $\sqrt{3.12} \approx$ 1.766， $\sqrt{31.2} \approx$ 5.586，则 $\sqrt{3120} \approx$ .

查看试题解析
14. 如图， $△ A B C$ 沿 $B C$ 方向平移后得到 $△ D E F$ ，已知 $B C = 10$ ， $E C = 3$ ，则平移的距离为．

查看试题解析
15. 如图，将一条两边互相平行的纸带折叠，若 $∠ 2$ 的度数为 $56 °$ ，则 $∠ 1$ 的度数为．

查看试题解析
16. 如图， $a ∥ b$ ，已知直角三角形 $A B C$ 中，B ， C在直线a上，A在直线b上， $A B = 3$ ， $A C = 4$ ， $B C = 5$ ，则点A到直线a的距离为．

查看试题解析

三、解答题（共72分）

17. 计算∶

(1)、 $\sqrt{2} - \sqrt{3} + \sqrt{3} + \sqrt{2}$ ；

(2)、 $\sqrt[3]{8} + \sqrt{{(- 2)}^{2}} - \sqrt{\frac{1}{9}}$ ；

查看试题解析
18. 求下列各式 $x$ 的值．

(1)、 $5 x^{2} = 125$ ；

(2)、 $8 (x + 1)^{3} = 27$ ；

查看试题解析
19. 解答题．

(1)、一个正数a的平方根是 $2 x - 4$ 与 $3 - x$ ，则a是多少？

(2)、已知a、b满足 $\sqrt{2 a + 8} + | b - \sqrt{3} | = 0$ ，求 $a + 2 b^{2}$ 平方根

查看试题解析
20. 如图，直线 $A B, C D$ 相交于点O ， $∠ A O C = 35 °$ ．

(1)、 $∠ A O C$ 的对顶角是； $∠ D O E$ 邻补角是；

(2)、若 $O A$ 平分 $∠ C O E$ ，求 $∠ B O E$ 的度数．

查看试题解析
21. 完成下面证明，并在下面括号里，填上推理的根据．
如图， $A D ∥ E F$ ， $∠ 1 + ∠ F E A = 180 °$ ．若 $∠ B A C = 80 °$ ．求 $∠ A G D$ 的度数．
解：∵ $A D ∥ E F$ （        ）
∴    ▲     $+ ∠ F E A = 180 °$ （        ）
∵ $∠ 1 + ∠ F E A = 180 °$
∴ $∠ 1 =$     ▲    （        ）
∴ $D G ∥ A B$ （        ）
∴ $∠ A G D +$     ▲     $= 180 °$ （        ）
∵    ▲    （已知）．
∴ $∠ A G D =$     ▲    （等式性质）

查看试题解析
22. 如图，用两个面积为 $200 c m^{2}$ 的小正方形拼成一个大的正方形．

(1)、则大正方形的边长是；

(2)、若沿着大正方形边的方向裁出一个长方形，能否使裁出的长方形纸片的长宽之比为 $4 : 3$ ，且面积为 $360 c m^{2}$ ？

查看试题解析
23. 如图， $A B ⊥ B F$ ， $C D ⊥ B F$ ， $∠ 1 = ∠ 2$ ， $∠ 3 = 60 °$ ．

(1)、求证： $C D ∥ E F$ ；

(2)、若 $A F$ 平分 $∠ B A E$ ，求 $∠ 2$ 的度数．

查看试题解析
24. 阅读下面的文字，解答问题：
大家知道 $\sqrt{2}$ 是无理数，而无理数是无限不循环小数，因此 $\sqrt{2}$ 的小数部分我们不可能全部写出来．将这个数减去其整数部分，差就是小数部分，因为 $\sqrt{2}$ 的整数部分是 $1$ ，于是用 $\sqrt{2} - 1$ 来表示 $\sqrt{2}$ 的小数部分．又例如：
∵ $\sqrt{4} < \sqrt{7} < \sqrt{9}$ ，即 $2 < \sqrt{7} < 3$
∴ $\sqrt{7}$ 的整数部分是2，小数部分为 $\sqrt{7} - 2$ $．$

(1)、 $\sqrt{26}$ 的整数部分是，小数部分是；

(2)、若 $m, n$ 分别是 $\sqrt{17} - 3$ 整数部分和小数部分，求 $3 m^{2} - n$ 的值．

查看试题解析
25. 已知∶直线 $E F$ 分别与直线 $A B$ ， $C D$ 相交于点 $G$ ， $H$ ，并且 $∠ A G E + ∠ D H E = 180 °$

(1)、如图1，求证∶ $A B ∥ C D$ ；

(2)、如图 2，点 $M$ 在直线 $A B$ ， $C D$ 之间，连接 $G M$ ， $H M$ ，求证∶ $∠ G M H = ∠ A G M + ∠ C H M$ ；

查看试题解析