四川省成都市新都区2024年中考数学一诊试卷

试卷更新日期：2024-04-16 类型：中考模拟

进入出卷网下载

一、选择题（本大题共8个小题，每小题4分，共32分；在每个小题给出的四个选项中，有且只有一个答案是符合题目要求的，并将自己所选答案的字母涂在答题卡上）

1. ﹣2024的绝对值是（　　）

A、2024 B、﹣2024 C、 $\frac{1}{2024}$ D、- $\frac{1}{2024}$

查看试题解析
2. 提高交通安全意识是每一位青少年的“必修课”，以下有关交通安全的标识图，既是轴对称图形，又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
3. 据统计，仅2024年大年初一这一天，我国全社会跨区域人员流动量约为1.9亿人次．将1.9亿用科学记数法表示为（　　）

A、19×10⁸ B、1.9×10⁹ C、0.19×10¹⁰ D、1.9×10⁸

查看试题解析
4. 下列各式计算正确的是（　　）

A、（x+y）²＝x²+y² B、（2x²）³＝6x⁶ C、4x³÷2x＝2x² D、x²﹣4y²＝（x+4y）（x﹣4y）

查看试题解析
5. 在平面直角坐标系中，点P（﹣2，﹣4）关于x轴对称的点的坐标是（　　）

A、（2，4） B、（0，﹣4） C、（﹣2，4） D、（2，﹣4）

查看试题解析
6. 2024年，中国将迎来一系列重要的周年纪念活动，某校开展了主题为“牢记历史•吾辈自强”的演讲比赛，九年级8名同学参加该演讲比赛的成绩分别为76，78，80，85，80，74，78，80．则这组数据的众数和中位数分别为（　　）

A、80，79 B、80，78 C、78，79 D、80，80

查看试题解析
7. 如图，点E是▱ABCD的边AD上一点，且AE：DE＝1：2，连接CE并延长，交BA的延长线于点F ．若AE＝4，AF＝6，则▱ABCD的周长为（　　）

A、21 B、34 C、48 D、60

查看试题解析
8. 已知抛物线y＝ax²+bx+c（a≠0）的对称轴为直线x＝﹣2，与x轴的一个交点坐标为（﹣4，0），其部分图象如图所示，下列结论：
①当x＜0时，y随x增大而增大；
②该抛物线一定过原点；
③b²﹣4ac＞0；
④a﹣b+c＜0；
⑤b＞0．
其中结论正确的个数有（　　）个．

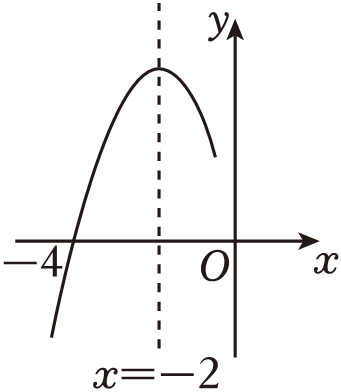A、1 B、2 C、3 D、4

查看试题解析

二、填空题（本大题共5个小题，每小题4分，共20分，答案写在答题卡上）

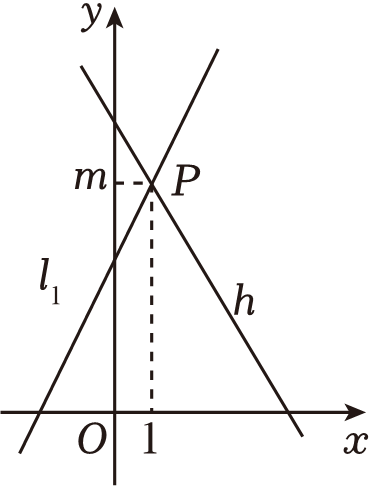
9. 分解因式：3a³﹣12a= ．

查看试题解析
10. 如图，直线：y＝2x+4与直线l₂：y＝kx+b相交于点P（1，m），则方程组 $\{\begin{array}{l} y - 2 x = 4 \\ y - k x = b \end{array}$ 的解为．

查看试题解析
11. 一个箱子装有除颜色外都相同的3个蓝球，3个灰球和一定数量的粉球．从中随机抽取1个球，被抽到粉球的概率是 $\frac{1}{2}$ ，那么箱内粉球有个．

查看试题解析
12. 如图，经过原点的直线交反比例函数的y= $\frac{k}{x}$ 图象于A ， B两点，过点A作AC⊥x轴于点C ，连接BC ，当S_△_ABC＝2时，k的值为．

查看试题解析
13. 如图，在Rt△ABC中，∠BAC＝90°，按以下步骤作图：①分别以点A和点C为圆心，大于 $\frac{1}{2}$ AC的长为半径作弧，两弧相交于M ， N两点；②作直线MN交BC于点D ，连接AD ．若AB＝BD＝2，则△ACD的面积为．

查看试题解析

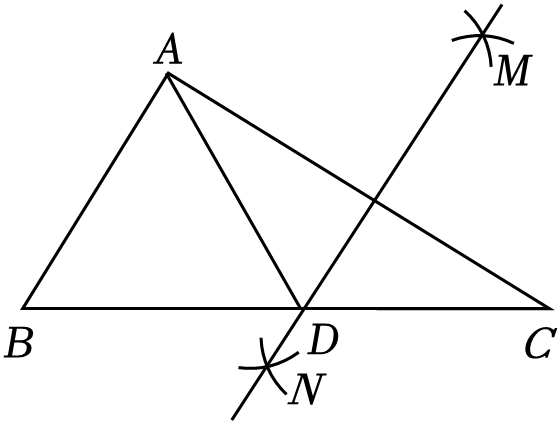
三、解答题（本大题共5小题，共48分，解答过程写在答题卡上）

14.

(1)、计算： $3 t a n 30^{\circ} - \sqrt{12} - \sqrt{2} c o s 45^{\circ} + {(\frac{π}{3} - 2024)}^{0}$ ；

(2)、先化简，再求值： $\frac{a^{2} - a}{a - 3} \div (\frac{6 a - 10}{a - 3} + a - 3)$ ，其中 $a = \sqrt{3} - 1$

查看试题解析
15. 为提升同学们的综合素质，丰富课余生活，某校举行了“爱新都”为主题的视频制作评比活动．某兴趣小组同学积极参与，计划制作有代表性景点的城市宣传短片，现抽样调查了部分学生，从A锦门民国小镇，B桂湖公园，C宝光寺，D新繁东湖，E泥巴沱公园五个景点中，选出最具有新都代表性的地方，并将调查情况绘制成如图两幅不完整统计图．
根据统计图中的信息解答下列问题：

(1)、本次被调查的学生有人，扇形统计图中表示A的扇形圆心角α的度数等于度，并把条形图补充完整；

(2)、该校学生共计1500人，请估算出该校认为最具有新都代表性的是宝光寺的学生人数；

(3)、该兴趣小组准备从校内四位“优秀共青团员”（两男两女）中，挑选两人作为宣传片中的讲解员，请利用列表或画树状图的方法，求所选两人恰好是1名男生和1名女生的概率．

查看试题解析
16. 某校学生利用课余时间，使用卷尺和测角仪测量某公园古城门的高度．如图所示，他们先在公园广场点M处架设测角仪，测得古城门最高点A的仰角为22°，然后前进20m到达点N处，测得点A的仰角为45°；已知测角仪的高度为1.4m ．求古城门最高点A距离地面的高度．（结果精确到0.1m；参考数据：sin22°≈0.37，cos22°≈0.93，tan22°≈0.40）

查看试题解析
17. 如图，已知矩形ABCD和矩形AEFG共用顶点A ，点E在线段BD上，连接EG ， DG ，且 $\frac{A B}{A D} = \frac{A E}{A G}$ ．

(1)、求证：∠ABE＝∠ADG；

(2)、若 $A B = \sqrt{3}, A D = \sqrt{15}, B E = \frac{1}{3} B D$ ，求EG的长．

查看试题解析
18. 在平面直角坐标系xOy 中，直线 $y = \frac{2}{3} x + b$ 与反比例函数 $y = \frac{12}{x}$ 的图象交于A（3，m），B两点．

(1)、求直线AB的函数表达式及点B的坐标；

(2)、如图1，过点A的直线分别与x轴，反比例函数y= $\frac{12}{x}$ 的图象（x＜0）交于点M ， N ，且 $\frac{A M}{M N} = \frac{4}{3}$ ，连接BM ，求△ABM的面积；

(3)、如图2，点D在另一条反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象上，点C在x轴正半轴上，连接DC交该反比例函数图象于点E ，且DE＝2EC ，再连接AD ， BC ，若此时四边形ABCD恰好为平行四边形，求k的值．

查看试题解析

四、填空题（本大题共5个小题，每小题4分，共20分，答案写在答题卡上）

19. 满足 $- \sqrt{3} < x < \sqrt{5}$ 的整数x有个．

查看试题解析
20. x₁ ， x₂为一元二次方程x（3x﹣1）﹣1＝0的两个实数根，则x₁+x₂﹣3x₁x₂＝．

查看试题解析
21. 将抛物线C₁：y＝x²向左平移a（a＞0）个单位长度后，再向下平移b个单位长度，得到新的抛物线C₂ ，若A（﹣a﹣2，y₁），B（﹣a+1，y₂），C（﹣a+3，y₃）为抛物线C₂图象上的三点，则y₁、y₂、y₃的大小关系.（请用“＜”表示）

查看试题解析
22. 如图1，以矩形ABCD的宽BC为边在其内部作正方形BCFE ，若 $\frac{A E}{A D} = \frac{A D}{A B}$ ，则称矩形ABCD为“黄金矩形”， $\frac{长}{宽} = \frac{A B}{A D} = \frac{1 + \sqrt{5}}{2}$ 称为“黄金比率”，如图2，以矩形ABCD的宽BC为边在其内部作两个正方形BCHG ， GHFE ，若 $\frac{A E}{A D} = \frac{A D}{A B}$ ，则称矩形ABCD为“白银矩形”， $\frac{长}{宽} = \frac{A B}{A D}$ 称为“白银比率”，则该比率为；如图3，A4纸的长与宽的比值近似可以看作 $\sqrt{2}$ ，若沿某条直线裁剪一次，使得A4纸剩下部分为一个“白银矩形”，则该“白银矩形”的面积是．

查看试题解析
23. 如图，在矩形ABCD中，BC＝2AB ，点M ， N为直线AD上的两个动点，且∠MBN＝30°，将线段BM关于BN翻折得线段BM^' ，连接CM^' ．当线段CM^'的长度最小时，∠MM'C的度数为度．

查看试题解析
24. 为了美化校园，某校准备在校园广场中心安装一个圆形喷水池，喷水池中央设置一柱形喷水装置OA高2米，点A处的喷头向外喷水，水流在各个方向上沿形状相同的抛物线路径落下．O位于圆形喷水池中心的水面处，按照如图所示建立直角坐标系，该设计水流与OA的水平距离为1米时，喷出的水柱可以达到最大高度3米．

(1)、求出该抛物线的函数表达式；

(2)、为了使喷出的水流不至于溅落在圆形喷水池外，需要在水流落回水面处的外侧预留1米距离，则该圆形喷水池的半径至少设计为多少米合理？

查看试题解析
25. 如图，在平面直角坐标系xOy 中，已知抛物线y＝ax²+c ，经过点M（2，3），与y轴交于点A（0，﹣1），直线BC与抛物线交于异于点A的B ， C两点．

(1)、求抛物线的函数表达式；

(2)、若三角形BOM是以OM为底的等腰三角形，试求出此时点B的横坐标；

(3)、若 BA⊥CA ，探究直线BC是否经过某一定点．若是，请求出该定点的坐标；若不是，请说明理由．

查看试题解析
26. 如图1，在四边形ABFE中，∠F＝90°，点C为线段EF上一点，使得AC⊥BC ， AC＝2BC＝4，此时BF＝CF ，连接BE ， BE⊥AE ，且AE＝BE ．

(1)、求CE的长度；

(2)、如图2，点D为线段AC上一动点（点D不与A ， C重合），连接BD ，以BD为斜边向右侧作等腰直角三角形BGD ．
①当DG∥AB时，试求AD的长度；
②如图3，点H为AB的中点，连接HG ，试问HG是否存在最小值，如果存在，请求出最小值；如果不存在，请说明理由．

查看试题解析