湖南省衡阳市蒸湘区2024年中考一模数学试题
试卷更新日期:2024-04-16 类型:中考模拟
一、选择题(每小题3分,10小题共30分,每小题只有一个正确答案)
-
1. 下列各式中,属于最简二次根式的是( )A、 B、 C、 D、2. 我市某一周的最高气温统计如下表:则这组数据的中位数与众数分别是( )
最高气温(℃)
25
26
27
28
天数
1
1
2
3
A、27,28 B、27.5,28 C、28,27 D、26.5,273. 已知点是外一点,且的半径为 , 则的长可能为( )A、 B、 C、 D、4. 某学校每年抽出资金购买书籍用于扩充图书室.已知2021年该校用于购买图书的费用为10000元,2023年用于购买图书的费用增加到14400元.设该校这两年购买图书的费用的年平均增长率为x , 据题意可列方程为( )A、 B、 C、 D、5. 如图,一架梯子斜靠在墙上,梯子的长为10米,梯子与地面形成的夹角为 , 则墙的高度为( )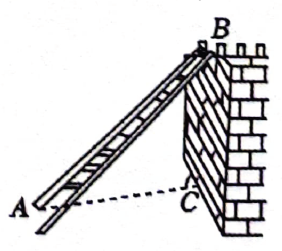 A、米 B、米 C、米 D、米6. 如图,点D在的边上,若要添加一个条件使得 , 则下列条件中不能满足要求的是( )
A、米 B、米 C、米 D、米6. 如图,点D在的边上,若要添加一个条件使得 , 则下列条件中不能满足要求的是( )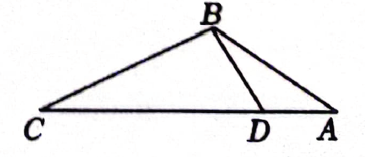 A、 B、 C、 D、7. 如图,在菱形中,E为边上一点,交于点O , 若 , 则等于( )
A、 B、 C、 D、7. 如图,在菱形中,E为边上一点,交于点O , 若 , 则等于( )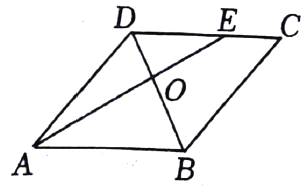 A、 B、 C、 D、8. 已知抛物线 , 下列结论中错误的是( )A、抛物线的开口向上 B、抛物线的对称轴为直线 C、当时,y随x的增大而减小 D、将抛物线向右平移2个单位,再向上平移3个单位,则得到的抛物线解析式为9. 如图是二次函数和一次函数的图象,当时,x的取值范围是( )
A、 B、 C、 D、8. 已知抛物线 , 下列结论中错误的是( )A、抛物线的开口向上 B、抛物线的对称轴为直线 C、当时,y随x的增大而减小 D、将抛物线向右平移2个单位,再向上平移3个单位,则得到的抛物线解析式为9. 如图是二次函数和一次函数的图象,当时,x的取值范围是( )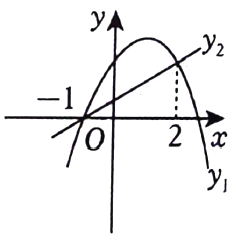 A、 B、 C、 D、或10. 如图,矩形中, , 点P是边上的一个动点(点P不与点B、C重合),现将沿直线折叠,使点C落在点处;作的平分线交于点E . 设 , 那么y关于x的函数图象大致应为( )
A、 B、 C、 D、或10. 如图,矩形中, , 点P是边上的一个动点(点P不与点B、C重合),现将沿直线折叠,使点C落在点处;作的平分线交于点E . 设 , 那么y关于x的函数图象大致应为( ) A、
A、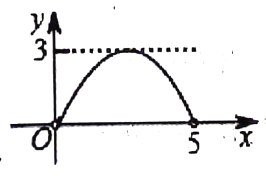 B、
B、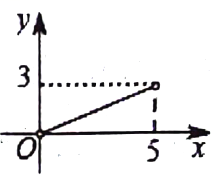 C、
C、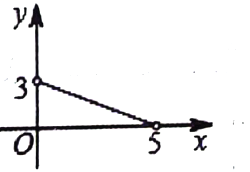 D、
D、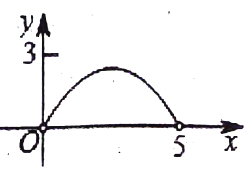
二、填空题(每小题3分,8小题,共24分)
-
11. 若二次根式 有意义,则x的取值范围是
12. 已知 , 那么 .13. 如图,在△ABC中,点D、E分别是AB、AC的中点.若DE=3,则BC= .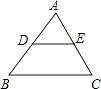 14. 一个底面半径是 , 母线长为的圆锥的侧面积为 .15. 如图,河堤横断面迎水坡的坡比是 , 堤高 , 则坡面的长度是 .
14. 一个底面半径是 , 母线长为的圆锥的侧面积为 .15. 如图,河堤横断面迎水坡的坡比是 , 堤高 , 则坡面的长度是 . 16. 如图,线段两个端点的坐标分别为 , 以原点O为位似中心,在第一象限内将线段放大到原来的2倍后得到线段 , 则端点C的坐标为 .
16. 如图,线段两个端点的坐标分别为 , 以原点O为位似中心,在第一象限内将线段放大到原来的2倍后得到线段 , 则端点C的坐标为 . 17. 如图,点A、B、C、D都在上, , 则 .
17. 如图,点A、B、C、D都在上, , 则 .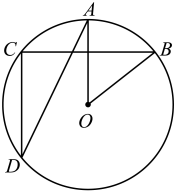 18. 在2023年中考体育考试前,小康对自己某次实心球的训练录像进行了分析,发现实心球飞行路线是一条抛物线,若不考虑空气阻力,实心球的飞行高度y(单位:米)与飞行的水平距离x(单位:米)之间具有函数关系 , 则小康这次实心球训练的成绩为 .
18. 在2023年中考体育考试前,小康对自己某次实心球的训练录像进行了分析,发现实心球飞行路线是一条抛物线,若不考虑空气阻力,实心球的飞行高度y(单位:米)与飞行的水平距离x(单位:米)之间具有函数关系 , 则小康这次实心球训练的成绩为 .
三、解答题(8小题,共66分)
-
19. 解方程20. 计算: .21. 随着移动互联网的迅猛发展,人们购物的支付方式更加多样、便捷.某商场想了解顾客支付方式的选择情况,设计了一份问卷进行调查,要求被调查者选择且只选择一种最喜欢的支付方式.现将调查结果绘制成如图所示的两幅不完整的统计图.请结合图中所给出的信息,解答下列问题:
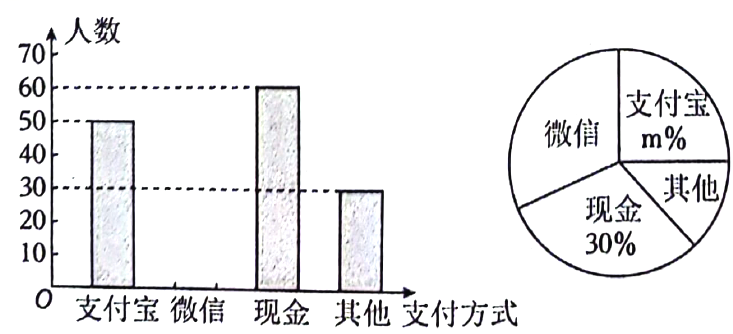 (1)、扇形统计图中 , “其他”支付方式所对应的圆心角为度;(2)、小明早上买早餐,若只能一种支付方式,刚好选择现金支付的概率为;(3)、甲乙两人到商场购物,请用列表或画树状图的方法,求出两人恰好都选择微信支付的概率.22. 关于x的一元二次方程有两个实数根 , 并且 .(1)、求实数m的取值范围;(2)、满足 , 求m的值.23. 为了增强学生体质、锤炼学生意志,某校组织二次定向越野拉练活动.如图,A点为出发点,途中设置两个检查点,分别为B点和C点,行进路线为 . B点在A点的南偏东方向处,C点在A点的北偏东方向,行进路线和所在直线的夹角为 .
(1)、扇形统计图中 , “其他”支付方式所对应的圆心角为度;(2)、小明早上买早餐,若只能一种支付方式,刚好选择现金支付的概率为;(3)、甲乙两人到商场购物,请用列表或画树状图的方法,求出两人恰好都选择微信支付的概率.22. 关于x的一元二次方程有两个实数根 , 并且 .(1)、求实数m的取值范围;(2)、满足 , 求m的值.23. 为了增强学生体质、锤炼学生意志,某校组织二次定向越野拉练活动.如图,A点为出发点,途中设置两个检查点,分别为B点和C点,行进路线为 . B点在A点的南偏东方向处,C点在A点的北偏东方向,行进路线和所在直线的夹角为 .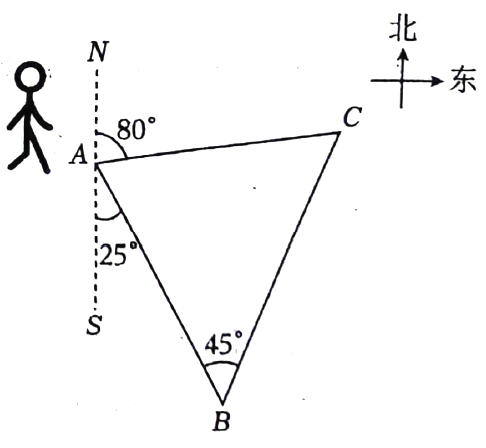 (1)、求行进路线和所在直线的夹角的度数;(2)、求检查点B和C之间的距离(结果保留根号).24. 如图,四边形是平行四边形,以边为直径的经过点C , E是上的一点,且 .
(1)、求行进路线和所在直线的夹角的度数;(2)、求检查点B和C之间的距离(结果保留根号).24. 如图,四边形是平行四边形,以边为直径的经过点C , E是上的一点,且 .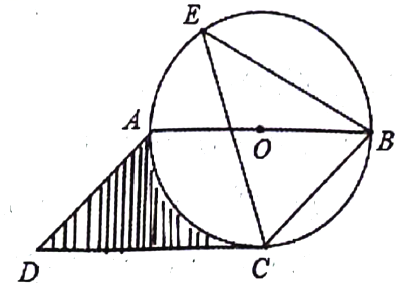 (1)、求证:是的切线;(2)、若 , 求的半径;(3)、在(2)的条件下,求阴影部分的面积.(结果保留π)25. 矩形在平面直角坐标系中的位置如图所示,点B、C在x轴上,交y轴于点E , 连接 , 线段的长是方程的两个根 .
(1)、求证:是的切线;(2)、若 , 求的半径;(3)、在(2)的条件下,求阴影部分的面积.(结果保留π)25. 矩形在平面直角坐标系中的位置如图所示,点B、C在x轴上,交y轴于点E , 连接 , 线段的长是方程的两个根 .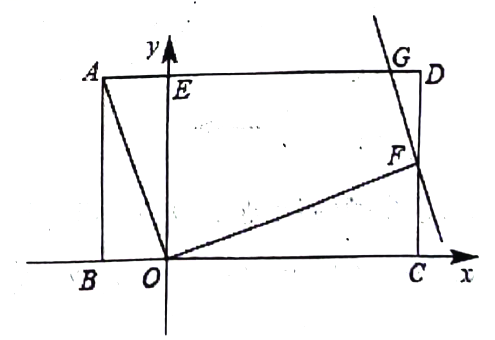 (1)、求点B、C的坐标;(2)、点F在边上,且F点的纵坐标是3,连接 , 过点F作直线 , 交于点G , 若矩形的面积等于66,双曲线的一个分支过点G , 求k的值;(3)、在(2)的条件下,在直线上并且在直线的右侧是否存在点P , 使得以O、F、P为顶点的三角形与相似.若存在,请求出点P坐标;若不存在,请说明理由.26. 定义:在平面直角坐标系中,当点N在图形M的内部,或在图形M上,且点N的横坐标和纵坐标相等时,则称点N为图形M的“梦之点”.
(1)、求点B、C的坐标;(2)、点F在边上,且F点的纵坐标是3,连接 , 过点F作直线 , 交于点G , 若矩形的面积等于66,双曲线的一个分支过点G , 求k的值;(3)、在(2)的条件下,在直线上并且在直线的右侧是否存在点P , 使得以O、F、P为顶点的三角形与相似.若存在,请求出点P坐标;若不存在,请说明理由.26. 定义:在平面直角坐标系中,当点N在图形M的内部,或在图形M上,且点N的横坐标和纵坐标相等时,则称点N为图形M的“梦之点”.图①
 图②
图② (1)、如图①,矩形的顶点坐标分别是 , 在点中,是矩形“梦之点”的是;(2)、如图②,已知点A、B是抛物线上的“梦之点”,点C是抛物线的顶点.连接 , 求的面积;(3)、在(2)的条件下,点P为抛物线上一点,点Q为平面内一点,是否存在点P、Q , 使得以为对角线,以A、B、P、Q为顶点的四边形是菱形?若存在,直接写出P点坐标;若不存在,请说明理由.
(1)、如图①,矩形的顶点坐标分别是 , 在点中,是矩形“梦之点”的是;(2)、如图②,已知点A、B是抛物线上的“梦之点”,点C是抛物线的顶点.连接 , 求的面积;(3)、在(2)的条件下,点P为抛物线上一点,点Q为平面内一点,是否存在点P、Q , 使得以为对角线,以A、B、P、Q为顶点的四边形是菱形?若存在,直接写出P点坐标;若不存在,请说明理由.