湖南省永州市道县2023-2024学年八年级下学期月考数学试题

试卷更新日期：2024-04-16 类型：月考试卷

进入出卷网下载

一、选择题（本题共10个小题，每小题只有一个正确答案，每小题3分，共30分）

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 一个多边形切去一个角后，形成的另一个多边形的内角和为 $1080 °$ ，原多边形的边数是（）

A、7或8或9 B、8或9或10 C、6或7或8 D、5或6或7

查看试题解析
3. 如图，已知△ABD ，用尺规进行如下操作：①以点B为圆心，AD长为半径画弧；②以点D为圆心，AB长为半径画弧；③两弧在BD上方交于点C ，连接BC ， DC ．可直接判定四边形ABCD为平行四边形的条件是（　　）

A、两组对边分别平行 B、两组对边分别相等 C、对角线互相平分 D、一组对边平行且相等

查看试题解析
4. 如图所示，在 $△ A B C$ 中， $A C = B C$ ， $A E = C D$ ， $A E ⊥ C E$ 于点 $E$ ， $B D ⊥ C D$ 于点 $D$ ， $A E = 7$ ， $B D = 2$ ，则 $D E$ 的长是（）

A、7 B、2 C、3 D、5

查看试题解析
5. 如图，在平行四边形 $A B C D$ 中，点 $E$ 是 $A D$ 的中点，对角线 $A C, B D$ 相交于点 $O$ ，连接 $O E$ ，若 $△ A B C$ 的周长是10，则 $△ A O E$ 的周长为（）

A、3 B、5 C、6 D、7

查看试题解析
6. $O C$ 为 $∠ A O B$ 的平分线， $M$ 为 $O B$ 上一点， $P$ 为 $O C$ 上一点，如果 $O M = 3$ ， $P M = 2$ ， $O P = \sqrt{13}$ ，那么点 $P$ 到射线 $O A$ 的距离为（）

A、1 B、 $\sqrt{13}$ C、2 D、3

查看试题解析
7. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A D$ 是 $∠ C A B$ 的平分线， $D E ⊥ A B$ 于点E ， $D E$ 平分 $∠ A D B$ ，则 $∠ B$ 等于（）

A、 $22.5 °$ B、 $30 °$ C、 $25 °$ D、 $40 °$

查看试题解析
8. 如图，平行四边形 $A B C D$ 中， $A B = 6$ ， $A D = 9$ ， $B E$ 平分 $∠ A B C$ ，交 $A D$ 于E ， $C F ⊥ B E$ 交 $B E$ 于点 $N$ ，交 $A D$ 于点 $F$ ，作 $M N / / C D$ 交 $A D$ 于点 $M$ ，则 $M N =$ （）

A、 $\frac{1}{2}$ B、 $\frac{2}{3}$ C、1 D、 $\frac{3}{2}$

查看试题解析
9. 如图，含 $30 °$ 角的三角尺（ $△ A B C$ ）的长直角边与含 $45 °$ 角的三角尺（ $△ A C D$ ）的斜边恰好重合， $A B$ 交 $C D$ 于点E．P，Q分别是边 $A C$ ， $B C$ 上的动点，当四边形 $E P Q B$ 为平行四边形时， $▱ E P Q B$ 的面积3，则线段 $C E$ 的长是（）

A、 $\sqrt{3}$ B、 $\sqrt{6}$ C、3 D、 $2 \sqrt{3}$

查看试题解析
10. 如图，在等边 $△ A B C$ 中， $A D ⊥ B C$ 于 $D$ ，延长 $B C$ 到 $E$ ，使 $C E = \frac{1}{2} B C$ ， $F$ 是 $A C$ 的中点，连接 $E F$ 并延长 $E F$ 交 $A B$ 于G ， $B G$ 的垂直平分线分别交 $B G$ ， $A D$ 于点 $M$ ，点 $N$ ，连接 $G N$ ， $G N$ ，下列结论：① $E G ⊥ A B$ ；② $G F = \frac{1}{2} E F$ ；③ $∠ G N C = 120 °$ ；④ $S_{四边形 A G N C} = 4 S_{△ M G N}$ ．其中正确的结论序号是（）．

A、①②③ B、②③④ C、①③④ D、①②③④

查看试题解析

二、填空题（本题共6小题，每小题3分，共18分）

11. 在四边形 $A B C D$ 中，现给出下列结论：
①若 $A B = C D$ ， $A D / / B C$ ，则四边形 $A B C D$ 是平行四边形；②若 $∠ A = ∠ C$ ， $∠ B = ∠ D$ ，则四边形 $A B C D$ 是平行四边形；③若 $A B / / C D$ ， $∠ A = ∠ C$ ，则四边形 $A B C D$ 是平行四边形；④ $A B = C D$ ， $∠ A = ∠ C$ ，则四边形 $A B C D$ 是平行四边形．
其中正确的结论是．（写出所有正确结论的序号）

查看试题解析
12. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ B A C$ 交 $B C$ 于 $D$ ．若 $B D : D C = 3 : 2$ ，点 $D$ 到 $A B$ 的距离为6，则 $B C$ 的长是．

查看试题解析
13. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ．按以下步骤作图：
①以点 $C$ 为圆心，适当长为半径画弧，分别交 $A C$ 、 $C B$ 于点M、N；
②分别以M、N为圆心，大于 $\frac{1}{2} M N$ 的长为半径画弧，两弧交于点 $F$ ；
③作射线 $C F$ ．若 $B C = 2$ ， $E$ 为 $B C$ 边的中点， $D$ 为射线 $C F$ 上一动点．则 $B D + D E$ 的最小值为．

查看试题解析
14. 如图，一个圆柱形水杯，底面直径为 $8 c m$ ，高为 $9 c m$ ，则一只小虫从下底点 $A$ 处爬到上底 $B$ 处，则小虫所爬的最短路径长是（ $π$ 取3） $c m$ ．

查看试题解析
15. 如图， $△ A B C$ 中， $∠ A C B = 90 °$ ， $D$ 为 $A C$ 边上的中点， $E$ 为 $A B$ 边上一点， $A B = 4 B E$ ，连接 $C E$ 、 $D E$ ，延长 $D E$ 交 $C B$ 延长线于 $F$ ，若 $B F = 3$ ， $A B = 10$ ，则 $C E^{2} =$ ．

查看试题解析
16. 如图，在▱ABCD 中，∠A＝60°，AB＝8，AD＝6，点 E、F 分别是边 AB、CD 上的动点，将该四边形沿折痕 EF 翻折，使点 A 落在边 BC 的三等分点处，则 AE 的长为．

查看试题解析

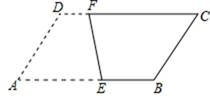
三、解答题（本大题共9个小题，共72分，解答题要求写出证明步骤或解答过程）

17. “儿童散学归来早，忙趁东风放纸再”．又到了放风筝的最佳时节．某校八年级（1）班的小明和小亮学习了“勾股定理”之后，为了测得风筝的垂直高度 $C E$ ，他们进行了如下操作：①测得水平距离 $B D$ 的长为15米；②根据手中剩余线的长度计算出风箏线 $B C$ 的长为25米；③牵线放风筝的小明的身高为1.6米．

(1)、求风筝的垂直高度 $C E$ ；

(2)、如果小明想风筝沿 $C D$ 方向下降12米，则他应该往回收线多少米？

查看试题解析
18. 如图，等腰直角三角形的直角边长都是8cm，以等腰直角三角形的两直角边为直径分别画两个半圆，则阴影部分的面积是多少（ $π$ 取3.14）？

查看试题解析
19. 已知：如图，四边形 $A B C D$ 为平行四边形，点E ， A ， C ， F在同一直线上， $A E = C F$ ．

(1)、求证： $△ A D E ≌ △ C B F$

(2)、连接 $B E$ 、 $D F$ ，求证：四边形 $B F D E$ 为平行四边形．

查看试题解析
20. 阅读下列材料，完成后面的任务：赵爽“弦”与完全平方公式
三国时期吴国的数学家赵爽创建了一幅“弦图”，如图所示该“弦图”由四个完全相同的直角三角形拼在一起得到一个大正方形和一个小正方形．已知直角三角形的两条直角边长分别为a ， b（ $a > b$ ），由图可知小正方形的边长为 $(a - b)$ ．
任务：

(1)、请你直接写出大正方形的面积（用含a ， b的代数式表示）

(2)、若 ${(a + b)}^{2} = 26$ ，大正方形的面积为17，求小正方形的面积．

查看试题解析
21. 如图，在平行四边形 $A B C D$ 中，点 $E$ 在 $A B$ 上，点 $F$ 在 $C D$ 上，且 $A E = C F$ ．

(1)、求证：四边形 $D E B F$ 是平行四边形；

(2)、若 $D E$ 为 $∠ A D C$ 的角平分线，且 $A D = 6$ ， $E B = 4$ ，求四边形 $A B C D$ 的周长．

查看试题解析
22. 如图，等腰直角 $△ A B C$ 中， $∠ A B C = 90 °$ ，点 $P$ 在 $A C$ 上，将 $△ A B P$ 绕顶点 $B$ 沿顺时针方向旋转 $90 °$ 后得到 $△ C B Q$ ．

(1)、求 $∠ P C Q$ 的度数．

(2)、当点 $P$ 在线段 $A C$ 上运动时（P不与A、C重合），请写出一个反映 $P A^{2}$ 、 $P C^{2}$ 、 $P B^{2}$ 之间关系的等式，并加以证明．

查看试题解析
23.

(1)、回归课本
请用文字语言表述三角形的中位线定理：．

(2)、回顾证法
证明三角形中位线定理的方法很多，但多数都要通过添加辅助线构图完成．下面是其中一种辅助线的添加方法．请结合图2，补全求证及证明过程．
已知：在 $△ A B C$ 中，点D ， E分别是 $A B, A C$ 的中点．
求证：_▲_．
证明：过点 $C$ 作 $C F / / A B$ ，与 $D E$ 的延长线交于点 $F$ ．

(3)、实践应用
如图3，点 $B$ 和点 $C$ 被池塘隔开，在 $B C$ 外选一点 $A$ ，连接 $A B, A C$ ，分别取 $A B, A C$ 的中点D ， E ，测得 $D E$ 的长度为9米，则B ， C两点间的距离为．

查看试题解析
24. 定义：若某三角形的三边长a ， b ， c满足 $a b + a^{2} = c^{2}$ ，则称该三角形为“类勾股三角形”．请根据以上定义解决下列问题：

(1)、判断等边三角形是否为“类勾股三角形”，并说明理由；

(2)、若等腰三角形 $A B C$ 是“类勾股三角形”，其中 $A C = B C$ ， $A B > A C$ ，求 $∠ A$ 的度数．

(3)、如图，在 $△ A B C$ 中， $∠ C = 2 ∠ A$ ，且 $∠ B > ∠ A$ ．证明： $△ A B C$ 为“类勾股三角形”．

查看试题解析
25. $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $C A = C B = 6$ ，点 $D$ 是 $R t △ A B C$ 直角边 $B C$ 所在直线 $l$ 上一点，连接 $A D$ ，以 $A D$ 为直角边向上作等腰 $△ A D E$ ， $∠ A D E = 90 °$ ， $A D = D E$ ，过点 $E$ 作 $E F ⊥ l$ ，垂足为 $F$ ．

(1)、如图1，当点 $D$ 在线段 $B C$ 上，且 $C D = 2$ 时，请你通过观察、测量、猜想，直接写出 $D F =$ ； $E F =$ ；

(2)、如图2，当点 $D$ 在线段 $B C$ 的延长线上，且 $C D = 2$ 时：
①请你由观察、猜想直接写出 $E F =$ _▲_；
②请你规范、严谨的证明： $C D = B F$ ．

(3)、如图3，当点 $D$ 在线段 $C B$ 的延长线上，且 $B D = 2$ 时，点 $P$ 为线段 $A D$ 上任意一点，以 $C P$ 为斜边向上做等腰 $R t △ C P G$ ， $C G = P G$ ， $∠ C G P = 90 °$ ，连接 $A G$ ，已知 $A D = 10$ ，请你直接写出当 $A G$ 长度最短时，线段 $A P$ 的值为．

查看试题解析