贵州省遵义市2023-2024学年八年级下学期4月月考数学试题

试卷更新日期：2024-04-16 类型：月考试卷

进入出卷网下载

一、选择题（本大题共12小题，每小题3分，共36分）

1. 若 $\sqrt{a + 1}$ 在实数范围内有意义，则 $a$ 的取值范围（　　　）

A、 $a \geq - 1$ B、 $a > - 1$ C、 $a \neq - 1$ D、 $a \leq - 1$

查看试题解析
2. 一直角三角形的两直角边长为6和8，则斜边长为（）

A、5 B、13 C、10 D、14

查看试题解析
3. 下列二次根式中与 $\sqrt{3}$ 是同类二次根式的是（）

A、 $\sqrt{12}$ B、 $\sqrt{0.3}$ C、 $\sqrt{\frac{2}{3}}$ D、 $\sqrt{18}$

查看试题解析
4. 如图，点A、B分别在直线a、b上，且直线 $a ∥ b$ ，以点A为圆心， $A B$ 长为半径画弧交直线a于点C ，连接 $B C$ ，若 $∠ 2 = 70 °$ ，则 $∠ 1 =$ （　　）

A、 $50 °$ B、 $40 °$ C、 $60 °$ D、 $70 °$

查看试题解析
5. 下列各式中属于最简二次根式的是（）

A、 $\sqrt{12}$ B、 $\sqrt{36}$ C、 $\sqrt{30}$ D、 $\sqrt{\frac{1}{2}}$

查看试题解析
6. 在 $△ A B C$ 中， $∠ A$ ， $∠ B$ ， $∠ C$ 的对边分别是a ， b ， c ，下列条件不能判定 $△ A B C$ 为直角三角形的是（）

A、 $∠ C = ∠ A + ∠ B$ B、 $∠ A = 35 °$ ， $∠ B = 65 °$ C、 $(b + c) (b - c) = a^{2}$ D、 $a = 3$ ， $b = 4$ ， $c = 5$

查看试题解析
7. 如图，有一个正方体盒子，棱长为 $1 cm$ ，一只蚂蚁从盒底点A沿盒的表面爬到盒顶的点B，蚂蚁爬行的最短路程是（）

A、 $\sqrt{5} cm$ B、 $3 cm$ C、 $\sqrt{3} cm$ D、 $2 cm$

查看试题解析
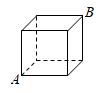8. 若 $\sqrt{a - 1} + b^{2} - 2 b + 1 = 0$ ，则ab的值等于（）

A、1 B、 $- 1$ C、2 D、 $- 2$

查看试题解析
9. 如图，每个小正方形的边长都是1，A，B，C分别在格点上，则∠ABC的度数为（）

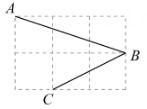A、30° B、45° C、50° D、60°

查看试题解析
10. 已知实数a在数轴上的位置如图所示，则化简： $| a - 2 | + \sqrt{{(a - 4)}^{2}}$ 的结果为（）

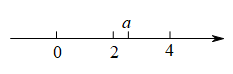A、2 B、-2 C、2a-6 D、-2a+6

查看试题解析
11. 甲、乙两艘客轮同时离开港口，航行的速度都是40m/min，甲客轮用15min到达点A，乙客轮用20min到达点B，若A，B两点的直线距离为1000m，甲客轮沿着北偏东30°的方向航行，则乙客轮的航行方向可能是（）

A、北偏西30° B、南偏西30° C、南偏东60° D、南偏西60°

查看试题解析
12. 如图，在四边形 $A B C D$ 中， $∠ A B C = ∠ A D C = 90 °$ ，分别以四边形的四条边为边向外作四个正方形，面积依次为 $S_{1}$ ， $S_{2}$ ， $S_{3}$ ， $S_{4}$ ，下列结论正确的是（）

A、 $S_{3} + S_{4} = 4 (S_{1} + S_{2})$ B、 $S_{1} - S_{2} = S_{3} - S_{4}$ C、 $S_{4} - S_{1} = S_{3} - S_{2}$ D、 $S_{4} - 3 S_{1} = S_{3} - 3 S_{2}$

查看试题解析

二、填空题（本大题共4个小题，每小题4分，共16分，请把正确答案填写在答题卡相应位置上．）

13. $\sqrt{5 n}$ 为整数，则正整数n的最小值为．

查看试题解析
14. 在平面直角坐标系中，点 $P (5, - 12)$ 到原点 $O (0, 0)$ 的距离是．

查看试题解析
15. 观察下列各式，第一个为 $\sqrt{2 \frac{2}{3}} = 2 \sqrt{\frac{2}{3}}$ ，第二个为 $\sqrt{3 \frac{3}{8}} = 3 \sqrt{\frac{3}{8}}$ ，第三个为 $\sqrt{4 \frac{4}{15}} = 4 \sqrt{\frac{4}{15}}$ ， $⋯$ 类比上述式子，根据规律，第七个式子为．

查看试题解析
16. 如图，在四边形ABCD中， $∠ B A D = ∠ B C D = 45 °$ ， $A B = 3 \sqrt{2}$ ， $A D = 7$ ， $C D = 5$ ，则 $A C =$ ．

查看试题解析

三、解答题（本大题共9小题，共98分，解答要写出必要的文字说明、证明过程或演算步骤）

17. 计算：

(1)、 $| - 2 | + \sqrt{9} + \frac{1}{2} \times \sqrt[3]{- 8}$ ；

(2)、 $\sqrt{4} - (\sqrt{2} - 1)^{0} - \sqrt[3]{27} + \sqrt{\frac{1}{25}}$ ．

查看试题解析
18. 现有5个边长为1的正方形，排列形式如图①，请把它们分割后拼接成一个新的正方形.要求：在图①中画出分割线并在图②正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.

查看试题解析
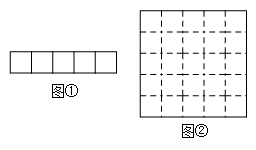19. 先化简，再求值： $(\frac{x + 1}{x^{2} - 1} + 1) \div \frac{x}{x^{2} - 2 x + 1}$ ，其中 $x = \sqrt{5} + 1$ ．

查看试题解析
20. 如图，某自动感应门的正上方A处装着一个感应器，离地的高度 $A B$ 为 $2.5$ 米，当人体进入感应器的感应范围内时，感应门就会自动打开．一个身高 $1.6$ 米的学生 $C D$ 正对门，缓慢走到离门 $1.2$ 米的地方时 $(B C = 1.2$ 米），感应门自动打开， $A D$ 为多少米？

查看试题解析
21. 阅读下列材料，然后回答问题．
在进行二次根式运算时，我们有时会碰上 $\frac{2}{\sqrt{3} + 1}$ 这样的式子，其实我们还可以将其进一步化简： $\frac{2}{\sqrt{3} + 1} = \frac{2 \times (\sqrt{3} - 1)}{(\sqrt{3} + 1) \times (\sqrt{3} - 1)} = \frac{2 \times (\sqrt{3} - 1)}{(\sqrt{3})^{2} - 1^{2}} = \sqrt{3} - 1$
以上这种化简的步骤叫作分母有理化．

(1)、化简 $\frac{2}{\sqrt{5} + \sqrt{3}}$ ；

(2)、已知 $\frac{1}{2 - \sqrt{3}}$ 的整数部分为a ，小数部分为b ，求 $a^{2} + b^{2}$ 的值．

查看试题解析
22. 如图四边形 $A B C D$ 中， $∠ A B C = 90 °, A B = 3, B C = 4, C D = 12, A D = 13$ ，求四边形 $A B C D$ 的面积．

查看试题解析
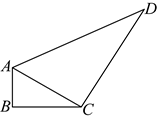23. 小明同学每次回家进入电梯间时，总能看见如图所示的提示“高空抛物害人害己”．为进一步研究高空抛物的危害，小明请教了物理老师，得知高空抛物下落的时间t（单位：s）和高度h（单位：m）近似满足公式 $t = \sqrt{\frac{2 h}{g}}$ （不考虑风速的影响， $g \approx 10 m / s^{2}$ ， $\sqrt{5} \approx 2.236$ ）

(1)、已知小明家住20层，每层的高度近似为3m，假如从小明家坠落一个物品，求该物品落地的时间；（结果保留根号）

(2)、小明查阅资料得知，伤害无防护人体只需要64焦的动能，高空抛物动能（焦） $= 10 \times$ 物体质量（千克） $\times$ 高度（米），某质量为0.1千克的玩具在高空被抛出后，最少经过几秒落地就可能会伤害到楼下的行人？

查看试题解析
24. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 6$ ， $B C = 8$ ， $D 、 E$ 分别是斜边 $A B$ 和直角边 $C B$ 上的点．把 $△ A B C$ 沿着直线 $D E$ 折叠，顶点 $B$ 的对应点是点 $B^{'}$ ．

(1)、如图1，若点 $B^{'}$ 和顶点 $A$ 重合，求 $C E$ 的长；

(2)、如图2，若点 $B^{'}$ 落在直角边 $A C$ 的中点上，求 $B E$ 的长．

查看试题解析
25. 我们定义：两边平方和等于第三边平方的两倍的三角形叫做“奇异三角形”．

(1)、根据“奇异三角形”的定义，请你判断命题：“等边三角形一定是奇异三角形”是命题．(填写“真命题、假命题”)

(2)、在RtΔABC 中， ∠ACB＝90°，AB＝c ， AC＝b ， BC＝a ，且b＞a ，若RtΔABC 是“奇异三角形”，则a：b：c＝．

(3)、如图，在四边形ACBD中，∠ACB=∠ADB=90°，AD=BD ，若在四边形ACBD内存在点E使得AE＝AD ， CB＝CE ．
①求证：ΔACE是“奇异三角形”；
②当ΔACE是直角三角形时，且AC＝ $\sqrt{3}$ ，求线段AB的长．

查看试题解析