2024年人教版初中数学八年级下学期期中重难点训练 06 正方形
试卷更新日期：2024-04-16 类型：同步测试
一、选择题
-
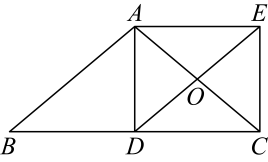
1. 下列命题正确的是（ ）A、一组对边平行，另一组对边相等的四边形是平行四边形 B、对角线相等的四边形是矩形 C、有一个角是直角的平行四边形是正方形 D、有一组邻边相等的平行四边形是菱形2. 如图，正方形中，以对角线为一边作菱形 ， 则等于（ ）
A、 B、 C、 D、3. 平行四边形、矩形、菱形、正方形都具有的性质是（ ）A、对角线互相垂直 B、对角线互相平分 C、对角线相等 D、对角线互相垂直平分且相等4. 如图，在边长为4的正方形ABCD中，∠CDE=30°，DE⊥CF，则AF 的长为 （ ）
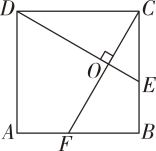A、 B、 C、 D、5. 如图，在正方形ABCD中，E，F 分别为AD，BC的中点，P为对角线BD上的一个动点，则下列线段的长等于AP+EP最小值的是 （ ）
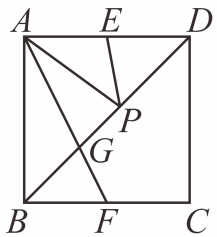A、AB B、DG C、BD D、AF6. 如图，在△ABC中，点D，E，F分别在边BC，AB，CA 上，且 DE∥CA，DF∥BA.有下列说法：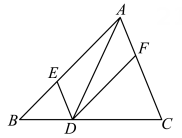
①四边形AEDF 是平行四边形；
②若∠BAC=90°，则四边形AEDF 是矩形；
③若 AD平分∠BAC，则四边形AEDF 是菱形；
④若AD⊥BC，且AB=AC，则四边形AEDF 是正方形.
其中正确的是 （ ）
A、①④ B、②③ C、①②③ D、①②③④7. 如图，M 是正方形ABCD 内的一点，且MC=MD =AD，则∠AMB的度数为 （ ）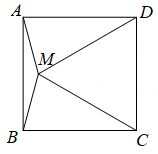
A、120° B、135° C、145° D、1508. 如图，正方形ABCD的边长为 10，AG=CH=8，BG=DH=6，连结GH，则GH 的长为 （ ）
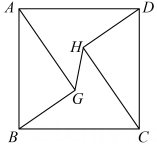A、 B、2 C、 D、二、填空题
-
9. 如图，正方形 ABCD的边长为 8，E 是 CD 的中点，连结 AE，AE的垂直平分线分别交AE，BC于点 H，G，则 BG的长为.
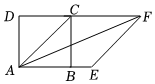
10. 如图，在正方形ABCD 中，△ABE为等边三角形，连结 DE，CE，延长 AE 交 CD 于点 F，则∠DEF的度数为°.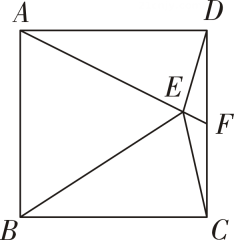
11. 如图，在矩形ABCD中，对角线AC，BD相交于点O，在不添加任何辅助线的情况下，请你添加一个条件 ， 使矩形ABCD是正方形．
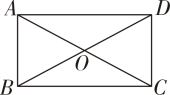12. 如图，在正方形的外侧，作等边三角形 ， 连接 ， ． 则 ．
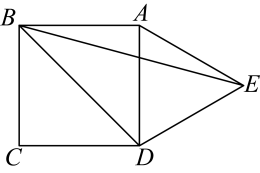13. 已知：正方形ABCD的边长为8，点E、F分别在AD、CD上，AE＝DF＝2，BE与AF相交于点G，点H为BF的中点，连接GH，则GH的长为.
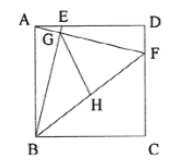14. 如图，正方形与正三角形的顶点重合，将绕其顶点旋转，在旋转过程中，当时，的大小是 ．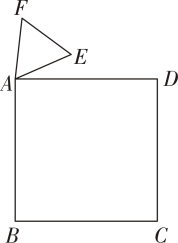
三、解答题
-
15. 如图，分别以△ABC的两边AB 和AC 为边向外作正方形ANMB 和正方形ACDE，连结NC，BE相交于点P.
(1)、求证：∠ANC=∠ABE.(2)、若BC=6，Q是线段BC 的中点，连结 PQ，则PQ=.16. 如图，在△ABC中，AB=AC，AD是BC 边上的中线，E 是 AD 上一点，过点 B作BF∥EC，交AD的延长线于点F，连结BE，CF.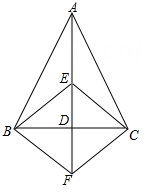
(1)、求证：△BDF≌△CDE.(2)、当 ED 与BC 满足什么数量关系时，四边形BECF 是正方形? 请说明理由.17. 如图，在矩形ABCD中，∠ABC，∠DCB的平分线的交点 E 落在边AD 上，BF∥CE，CF∥BE.求证：四边形 BECF 是正方形.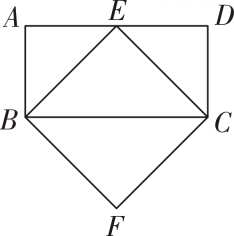
四、实践探究题
-
18. 如图①，的顶点P是正方形两条对角线的交点， ， 将绕点P旋转，旋转过程中的两边分别与正方形的边和交于点E和点F（点F与点C，D不重合）
(1)、如图①，当时，之间满足的数量关系是；(2)、如图②，将图①中的正方形改为的菱形，M是中点，其他条件不变，当时，求证： ．(3)、在（2）的条件下，若旋转过程中的边与线段延长线交于点E，其他条件不变，探究在整个运动变化过程中，之间满足的数量关系．五、综合题
