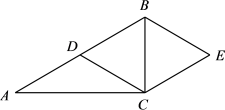2024年人教版初中数学八年级下学期期中重难点训练 05 菱形
试卷更新日期:2024-04-16 类型:同步测试
一、选择题
-
1. 菱形不具有的性质是( )A、对角相等 B、对边平行 C、对角线互相垂直 D、对角线相等2. 下列说法中正确的是( )A、有一组对边平行的四边形是平行四边形 B、对角线互相垂直的四边形是菱形 C、有一组邻边相等的平行四边形是菱形 D、对角线互相垂直平分的四边形是矩形3. 如图,四边形 ABCD的对角线互相平分,要使它变为菱形,还需要添加的条件是( )
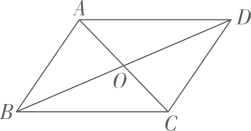 A、AB=CD B、AD=BC C、AC=BD D、AB=BC4. 如图,丝带重叠的部分一定是( )
A、AB=CD B、AD=BC C、AC=BD D、AB=BC4. 如图,丝带重叠的部分一定是( ) A、正方形 B、矩形 C、菱形 D、都有可能5. 如图,菱形ABCD中,E、F分别是AB、AC的中点,若EF=3,则菱形ABCD的周长为( )
A、正方形 B、矩形 C、菱形 D、都有可能5. 如图,菱形ABCD中,E、F分别是AB、AC的中点,若EF=3,则菱形ABCD的周长为( )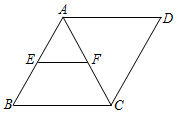 A、24 B、18 C、12 D、96. 如图,菱形ABCD中,过点作交BD于点 , 若 , 则( )
A、24 B、18 C、12 D、96. 如图,菱形ABCD中,过点作交BD于点 , 若 , 则( ) A、 B、 C、 D、7. 如图,在矩形ABCD中,E,F分别是AD,BC的中点,AF 与BE,CE与DF 分别相交于点M,N,则四边形 EMFN是( )
A、 B、 C、 D、7. 如图,在矩形ABCD中,E,F分别是AD,BC的中点,AF 与BE,CE与DF 分别相交于点M,N,则四边形 EMFN是( ) A、正方形 B、菱形 C、矩形 D、一般的平行四边形8. 如图,在菱形ABCD中,点E是AB边上一点,且 , 有下列结论:①;②是等边三角形;②是等腰三角形;④.其中结论正确的个数是( )
A、正方形 B、菱形 C、矩形 D、一般的平行四边形8. 如图,在菱形ABCD中,点E是AB边上一点,且 , 有下列结论:①;②是等边三角形;②是等腰三角形;④.其中结论正确的个数是( )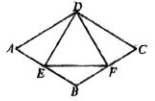 A、3个 B、4个 C、1个 D、2个
A、3个 B、4个 C、1个 D、2个二、填空题
-
9. 如图,在四边形ABCD中,对角线AC与BD相交于点平分.给出下列两个条件:① , ②;从二者中选择一个作为补充条件,使四边形ABCD是菱形,这个条件是.(填写序号)
 10. 如图,菱形ABCD的对角线AC,BD相交于点O,已知AC=24,BD=10,则菱形 ABCD的周长为.
10. 如图,菱形ABCD的对角线AC,BD相交于点O,已知AC=24,BD=10,则菱形 ABCD的周长为. 11. 如图,菱形ABCD的周长是16,∠ABC=60°,则对角线 AC的长为.
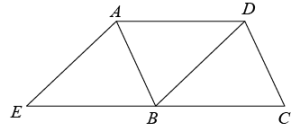
11. 如图,菱形ABCD的周长是16,∠ABC=60°,则对角线 AC的长为. 12. 如图将△ABC沿着BC方向平移得到△DEF,只需添加一个条件即可证明四边形ABED是菱形,这个条件可以是(写出一个即可).
12. 如图将△ABC沿着BC方向平移得到△DEF,只需添加一个条件即可证明四边形ABED是菱形,这个条件可以是(写出一个即可).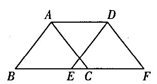 13. 如图,在菱形ABCD中,E是边CD上一点,连结AE 交对角线 BD 于点F,连结CF.若∠AED=40°,则∠BCF的度数为°.
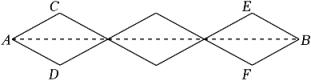
13. 如图,在菱形ABCD中,E是边CD上一点,连结AE 交对角线 BD 于点F,连结CF.若∠AED=40°,则∠BCF的度数为°.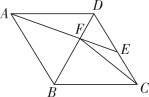 14. 如图,是一个菱形衣挂的平面示意图,每个菱形的边长为16cm,当锐角时,把这个衣挂固定在墙上,两个钉子CE之间的距离是cm.(结果保留根号)
14. 如图,是一个菱形衣挂的平面示意图,每个菱形的边长为16cm,当锐角时,把这个衣挂固定在墙上,两个钉子CE之间的距离是cm.(结果保留根号)
三、解答题
-
15. 如图,在ABCD平行四边形中,过点A作于点E,于点F, . 求证:
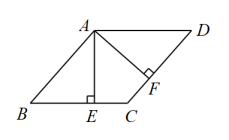 (1)、;(2)、四边形ABCD是菱形.16. 如图,四边形中, , 点为对角线的中点,过点的直线分别与、所在的直线相交于点、 . (点不与点重合)
(1)、;(2)、四边形ABCD是菱形.16. 如图,四边形中, , 点为对角线的中点,过点的直线分别与、所在的直线相交于点、 . (点不与点重合) (1)、求证:;(2)、当直线时,连结、 , 试判断四边形的形状,并说明理由.17. 如图,▱ABCD的对角线AC,BD相交于点O,过点O作AC 的垂线,分别交 AB,DC 于点E,F,连结AF,CE.
(1)、求证:;(2)、当直线时,连结、 , 试判断四边形的形状,并说明理由.17. 如图,▱ABCD的对角线AC,BD相交于点O,过点O作AC 的垂线,分别交 AB,DC 于点E,F,连结AF,CE.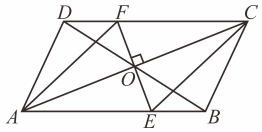 (1)、若 求EF的长.(2)、判断四边形AECF 的形状,并说明理由.
(1)、若 求EF的长.(2)、判断四边形AECF 的形状,并说明理由.四、实践探究题
-
18. 课本再现
思考
我们知道,菱形的对角线互相垂直.反过来,对角线互相垂直的平行四边形是菱形吗?
可以发现并证明菱形的一个判定定理;
对角线互相垂直的平行四边形是菱形.
(1)、定理证明为了证明该定理,小明同学画出了图形(如图1),并写出了“已知”和“求证”,请你完成证明过程.
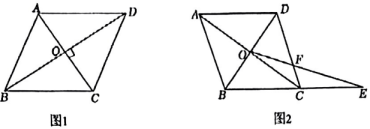
已知:在中,对角线 , 垂足为.
求证:是菱形.
(2)、知识应用如图2,在中,对角线AC和BD相交于点.求证:是菱形.
五、综合题