2024年人教版初中数学八年级下学期期中重难点训练 04 矩形
试卷更新日期:2024-04-16 类型:同步测试
一、选择题
-
1. 已知矩形的一边长为6cm,一条对角线的长为10 cm,则矩形的面积为( )A、12 cm2 B、24 cm2 C、48 cm2 D、60 cm22. 面积为的长方形一边长为另一边长为( )A、 B、 C、 D、3. 如图,平行四边形ABCD的对角线AC与BD相交于点O,添加一个条件使平行四边形ABCD为矩形的是( )
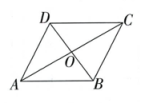 A、AD=AB B、AB⊥AD C、AB=AC D、CA⊥BD4. 一技术人员用刻度尺(单位:cm)测量某三角形部件的尺寸.如图所示,已知∠ACB=90°,D为边AB的中点,点A,B对应的刻度分别为1,7,则CD=( )
A、AD=AB B、AB⊥AD C、AB=AC D、CA⊥BD4. 一技术人员用刻度尺(单位:cm)测量某三角形部件的尺寸.如图所示,已知∠ACB=90°,D为边AB的中点,点A,B对应的刻度分别为1,7,则CD=( )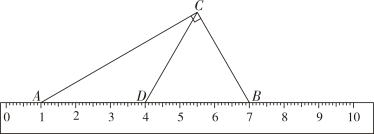 A、3.5cm B、3cm C、4.5cm D、6cm.5. 如图,在矩形中,、相交于点O , 平分交于点E , 若 , 则的度数为( )
A、3.5cm B、3cm C、4.5cm D、6cm.5. 如图,在矩形中,、相交于点O , 平分交于点E , 若 , 则的度数为( ) A、 B、 C、 D、6. 如图,在一块长14m、宽6m的长方形场地上,有一条弯曲的道路,其余的部分为绿化区,道路的左边线向右平移3m就是它的右边线,则绿化区的面积是( )
A、 B、 C、 D、6. 如图,在一块长14m、宽6m的长方形场地上,有一条弯曲的道路,其余的部分为绿化区,道路的左边线向右平移3m就是它的右边线,则绿化区的面积是( ) A、 B、 C、 D、7. 如图,矩形ABCD中,E,F,G,H分别在AB,BC,CD,DA上,且 , 若矩形ABCD面积为9,则四边形EFGH的面积为( )
A、 B、 C、 D、7. 如图,矩形ABCD中,E,F,G,H分别在AB,BC,CD,DA上,且 , 若矩形ABCD面积为9,则四边形EFGH的面积为( ) A、3 B、4 C、5 D、68. 如图,在矩形中, , 的平分线交于点 . 于点 , 连接并延长交于点 , 连接交于点 , 下列结论:
A、3 B、4 C、5 D、68. 如图,在矩形中, , 的平分线交于点 . 于点 , 连接并延长交于点 , 连接交于点 , 下列结论:
①;①;③;④;⑤ ,
其中正确的有( )
A、2个 B、3个 C、4个 D、5个二、填空题
-
9. 如图,中, , , , D为斜边AB的中点,则CD的长是 .
 10. 如图,在中,是边上的高线,是边上的中线,于点G, , 若 , , 则的面积是.
10. 如图,在中,是边上的高线,是边上的中线,于点G, , 若 , , 则的面积是.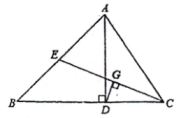 11. 如图所示,在 中, , 是斜边 上的中线, 分别为 的中点,若 ,则 .
11. 如图所示,在 中, , 是斜边 上的中线, 分别为 的中点,若 ,则 . 12. 如图,在矩形ABCD中,AC,BD相交于点O,M,N 分别为BC,OC 的中点,若MN=4,则AO 的长为
12. 如图,在矩形ABCD中,AC,BD相交于点O,M,N 分别为BC,OC 的中点,若MN=4,则AO 的长为 13. 如图,已知▱ABCD的对角线 AC,BD 相交于点O,△AOB 是等边三角形,AB=4,则▱ABCD的面积为 .
13. 如图,已知▱ABCD的对角线 AC,BD 相交于点O,△AOB 是等边三角形,AB=4,则▱ABCD的面积为 . 14. 如图,在△ABC中,∠ACB=90°,点D在边AB上(不与点A,B重合),DE⊥AC于点E,DF⊥BC于点F,连结EF.若AC=3,BC=2,则EF的最小值为.
14. 如图,在△ABC中,∠ACB=90°,点D在边AB上(不与点A,B重合),DE⊥AC于点E,DF⊥BC于点F,连结EF.若AC=3,BC=2,则EF的最小值为.
三、解答题
-
15. 已知一个长方形相邻的两边长分别是a , b , 且 , ;(1)、求此长方形的周长;(2)、若一个正方形的周长与上述长方形的周长相等,求此正方形的面积.16. 如图,在▱ABCD中,E为BC的中点,连结AE并延长交 DC 的延长线于点 F,连结 BF,AC.若AD=AF,求证:四边形ABFC 是矩形.
 17. 如图,在矩形ABCD 中,E,F分别是边 BC,AD 上的点,且AE=CF.
17. 如图,在矩形ABCD 中,E,F分别是边 BC,AD 上的点,且AE=CF. (1)、求证:△ABE≌△CDF.(2)、当AC⊥EF时,四边形 AECF 是菱形吗? 请说明理由.
(1)、求证:△ABE≌△CDF.(2)、当AC⊥EF时,四边形 AECF 是菱形吗? 请说明理由.四、实践探究题
-
18. 综合与实践

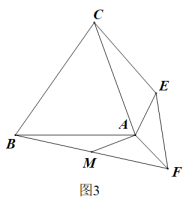
【问题情境】
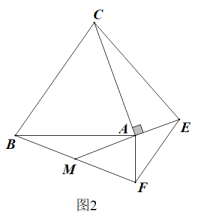
如图1,有两张等腰三角形纸片ABC和AEF,其中AB=AC,AE=AF,∠BAC+∠EAF=180°.△AEF绕着A顺时针旋转,旋转角为(),点M为BF的中点.
【特例感知】
(1)、如图1,当时,AM和CE的数量关系是;(2)、如图2,当时,连接AM,CE,请判断AM和CE的数量关系,并说明理由;(3)、【深入探究】如图3,当为任意锐角时,连接AM,CE,则(2)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.
19. 【操作】如图①,在矩形中,E为对角线上的一点(不与点A重合).将沿射线方向平移到的位置,点E的对应点为点F,易证:(不需要证明);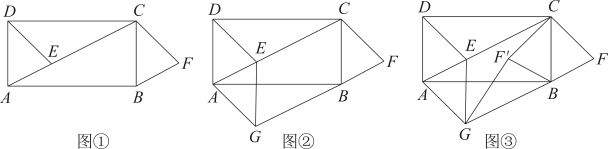
【探究】过图①的点E作 , 交的延长线于点G,连接 , 其他条件不变,如图②.求证:;
【拓展】将图②中的沿翻折得到 , 连接 , 其他条件不变,如图③.当最短时,若 , , 直接写出四边形的周长.
五、综合题

