2024年人教版初中数学八年级下学期期中重难点训练 03平行四边形
试卷更新日期:2024-04-16 类型:同步测试
一、选择题
-
1. 下列条件中,不能判定一个四边形是平行四边形的是( )A、两组对边分别平行 B、一组对边平行,另一组对边相等 C、一组对边平行且相等 D、两组对边分别相等2. 如图,在四边形ABCD中,AD∥BC,添加下列条件后,不能判定四边形ABCD一定是平行四边形的是( )
 A、AD=BC B、AB=DC C、AB∥CD D、∠B=∠D3. 如图,在中,点E , F分别为 , 的中点,若的长为 , 则的长为( )
A、AD=BC B、AB=DC C、AB∥CD D、∠B=∠D3. 如图,在中,点E , F分别为 , 的中点,若的长为 , 则的长为( )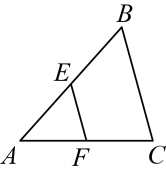 A、 B、2 C、 D、44. 在中,若 , 则的度数是( )
A、 B、2 C、 D、44. 在中,若 , 则的度数是( ) A、70° B、110° C、120° D、140°5. 原命题“平行四边形的两组对角分别相等”和它的逆命题“两组对角分别相等的四边形是平行四边形”,下列说法正确的是( )A、原命题和逆命题都正确 B、原命题和逆命题都错误 C、原命题错误,逆命题正确 D、原命题正确,逆命题错误6. 如图,在□中 , 平分 , 交边于点 , 过点作于点 , 交于点 . 若 , 则的长为( )
A、70° B、110° C、120° D、140°5. 原命题“平行四边形的两组对角分别相等”和它的逆命题“两组对角分别相等的四边形是平行四边形”,下列说法正确的是( )A、原命题和逆命题都正确 B、原命题和逆命题都错误 C、原命题错误,逆命题正确 D、原命题正确,逆命题错误6. 如图,在□中 , 平分 , 交边于点 , 过点作于点 , 交于点 . 若 , 则的长为( ) A、8 B、10 C、12 D、167. 如图,在中,是的中线,分别是的中点,连接 . 已知 , 则的长为( )
A、8 B、10 C、12 D、167. 如图,在中,是的中线,分别是的中点,连接 . 已知 , 则的长为( ) A、2 B、4 C、6 D、88. 如图,四边形ABCD中,为BC延长线上一点,连接AE,AE交CD于点的平分线交AE于点G.若为CD的中点,6,则AC的值为( )
A、2 B、4 C、6 D、88. 如图,四边形ABCD中,为BC延长线上一点,连接AE,AE交CD于点的平分线交AE于点G.若为CD的中点,6,则AC的值为( ) A、9 B、 C、10 D、9. 如图,在中,对角线、相交于点 , 平分 , 分别交、于点、 , 连接 , , , 则下列结论:① , ② , ③ , ④ . 其中正确的有( )
A、9 B、 C、10 D、9. 如图,在中,对角线、相交于点 , 平分 , 分别交、于点、 , 连接 , , , 则下列结论:① , ② , ③ , ④ . 其中正确的有( ) A、1个 B、2个 C、3个 D、4个10. 如图,在中, , , 平分 , 对角线相交于点O,连接 , 下列结论中正确的有( )
A、1个 B、2个 C、3个 D、4个10. 如图,在中, , , 平分 , 对角线相交于点O,连接 , 下列结论中正确的有( )①;②;③;④;⑤
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 如图,▱ABCD的对角线AC,BD相交于点O,E是AB的中点,的周长是8,则的周长为.
 12. 如图,在△ABC中,AB=AC=10,BC=16,D,E分别是AB,AC的中点,BF平分∠ABC,交DE于点F,连接AF,则AF=.
12. 如图,在△ABC中,AB=AC=10,BC=16,D,E分别是AB,AC的中点,BF平分∠ABC,交DE于点F,连接AF,则AF=. 13. 如图,在▱ABCD中,过点 B 作 BM⊥AC 于点E,交 CD于点 M,过点 D作 DN⊥AC 于点 F,交 AB于点 N,AF=12,EM=5.若 AD=15,则直线AB 与CD之间的距离为.
13. 如图,在▱ABCD中,过点 B 作 BM⊥AC 于点E,交 CD于点 M,过点 D作 DN⊥AC 于点 F,交 AB于点 N,AF=12,EM=5.若 AD=15,则直线AB 与CD之间的距离为. 14. 如图,在□ABCD中,过对角线 BD上一点 P 作EF∥AB,GH∥AD,与各边的交点分别为E,F,G,H.若▱ABCD的面积为 40,四边形BGPF的面积为 5,四边形 PEDH 的面积为21,则四边形 AGPE 的面积为.
14. 如图,在□ABCD中,过对角线 BD上一点 P 作EF∥AB,GH∥AD,与各边的交点分别为E,F,G,H.若▱ABCD的面积为 40,四边形BGPF的面积为 5,四边形 PEDH 的面积为21,则四边形 AGPE 的面积为. 15. 如图,四边形是平行四边形,以点为圆心,的长为半径作弧交于点 , 分别以点、为圆心,大于的长为半径作弧,两弧交于点 , 作射线交的延长线于点 , , , 则的长为 .
15. 如图,四边形是平行四边形,以点为圆心,的长为半径作弧交于点 , 分别以点、为圆心,大于的长为半径作弧,两弧交于点 , 作射线交的延长线于点 , , , 则的长为 .
三、解答题
-
16. 如图,▱ABCD的对角线AC,BD相交于点O,点E,F在AC上,且AE=CF.
 (1)、求证:BE∥DF;(2)、过点O作OM⊥BD,垂足为O,交DF于点M,若△BFM的周长为12,求四边形BEDF的周长.17. 已知:如图,在▱ABCD中,过 AC的中点O的直线分别交 CB,AD 的延长线于点 E,F.求证:BE=DF.
(1)、求证:BE∥DF;(2)、过点O作OM⊥BD,垂足为O,交DF于点M,若△BFM的周长为12,求四边形BEDF的周长.17. 已知:如图,在▱ABCD中,过 AC的中点O的直线分别交 CB,AD 的延长线于点 E,F.求证:BE=DF.
四、实践探究题
-
18. 如图
 (1)、【教材呈现】如图是华师版八年级下册数学教材第页练习的部分内容.
(1)、【教材呈现】如图是华师版八年级下册数学教材第页练习的部分内容.如图 , 如果直线 , 那么的面积和的面积是相等的.
 (2)、【方法探究】如图 , 在▱中,点在边上若 , 求与数量关系.(3)、【方法应用】如图 , 正方形的边长为 , 点是正方形内部一点,连结、当是以为腰的等腰三角形,且时,直接写出的长.
(2)、【方法探究】如图 , 在▱中,点在边上若 , 求与数量关系.(3)、【方法应用】如图 , 正方形的边长为 , 点是正方形内部一点,连结、当是以为腰的等腰三角形,且时,直接写出的长.五、综合题
-
19. 如图,在平行四边形中, , 点E为边上一点,连结交对角线于点F.(1)、如图,若 , , 求的长度;
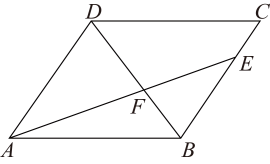 (2)、如图,若 , 点G,H为边的两点,连接 , , , 且满足 . 求证: .
(2)、如图,若 , 点G,H为边的两点,连接 , , , 且满足 . 求证: .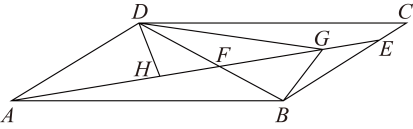 (3)、如图,若 , , 将沿射线方向平移,得到 , 连接 , , 当的值最小时,请直接写出的最小值.
(3)、如图,若 , , 将沿射线方向平移,得到 , 连接 , , 当的值最小时,请直接写出的最小值.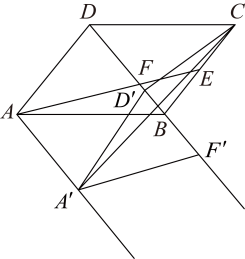
-