2024年初中数学人教版七年级下学期期中模拟考试卷 05
试卷更新日期:2024-04-16 类型:期中考试
一、单选题
-
1. 下列各数中是无理数的是( )A、 B、 C、 D、2. 下列命题中:①两个角的和等于平角时,这两个角互为补角,②同位角相等,③两条平行线被第三条直线所截,内错角相等,其中是真命题的个数是( )A、0个 B、1个 C、2个 D、3个3. 有理数在数轴上的位置如图所示,下列各数中,可能在0到1之间的是( )
 A、 B、 C、 D、4. 光线从空气射入水中时,光线的传播方向会发生改变,这就是折射现象.如图,水面MN与底面EF平行,光线AB从空气射入水里时发生了折射,变成了光线BC射到水底C处,射线BD是光线AB的延长线,若 , , 则的度数为( )
A、 B、 C、 D、4. 光线从空气射入水中时,光线的传播方向会发生改变,这就是折射现象.如图,水面MN与底面EF平行,光线AB从空气射入水里时发生了折射,变成了光线BC射到水底C处,射线BD是光线AB的延长线,若 , , 则的度数为( ) A、 B、 C、 D、5. 实数a在数轴上的对应点的位置如图所示.若 , 则b的值可以是( )
A、 B、 C、 D、5. 实数a在数轴上的对应点的位置如图所示.若 , 则b的值可以是( )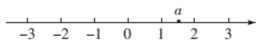 A、 B、0 C、1 D、26. 如图,直线被直线所截, , , 则的度数为( )
A、 B、0 C、1 D、26. 如图,直线被直线所截, , , 则的度数为( )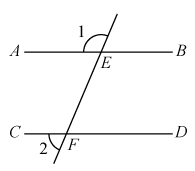 A、 B、 C、 D、7. 如图,在数轴上点A表示的实数是( )
A、 B、 C、 D、7. 如图,在数轴上点A表示的实数是( ) A、 B、 C、 D、8. 如图,AB CD,∠ABE= ∠EBF,∠DCE= ∠ECF,设∠ABE=α,∠E=β,∠F=γ,则α,β,γ的数量关系是( )
A、 B、 C、 D、8. 如图,AB CD,∠ABE= ∠EBF,∠DCE= ∠ECF,设∠ABE=α,∠E=β,∠F=γ,则α,β,γ的数量关系是( )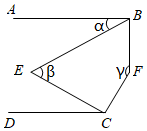 A、4β﹣α+γ=360° B、3β﹣α+γ=360° C、4β﹣α﹣γ=360° D、3β﹣2α﹣γ=360°
A、4β﹣α+γ=360° B、3β﹣α+γ=360° C、4β﹣α﹣γ=360° D、3β﹣2α﹣γ=360°二、填空题
-
9. 比较大小: .(填“>、<、或=”)10. 已知点P的坐标为(4,5),则点P到x轴的距离是 .11. 如图,一块长方形草地的长为 , 宽为 , 草地中间有一条弯曲的小路,小路的左边线向右平移2m就是它的右边线,则这块草地的绿地面积为 .
 12. 阅读下列材料:因为 , 即 , 所以的整数部分为2,小数部分为 , 若规定实数m的整数部分记为 , 小数部分记为 , 可得: , . 按照此规定计算的值 .13. 如图,已知AB∥CD,BE、DE分别平分∠ABF、∠CDF,∠F=40°,则∠E= .
12. 阅读下列材料:因为 , 即 , 所以的整数部分为2,小数部分为 , 若规定实数m的整数部分记为 , 小数部分记为 , 可得: , . 按照此规定计算的值 .13. 如图,已知AB∥CD,BE、DE分别平分∠ABF、∠CDF,∠F=40°,则∠E= .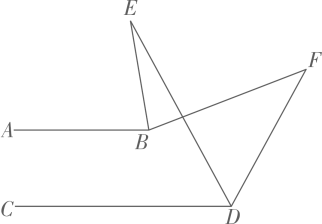 14. 如图,点D是射线上一动点,连接 , 过点D作交直线于点E , 若 , , 则的度数为 .
14. 如图,点D是射线上一动点,连接 , 过点D作交直线于点E , 若 , , 则的度数为 .
三、计算题
-
15. 计算: .
四、作图题
-
16. 如图,这是一个被抹去了平面直角坐标系的网格图,网格中每个小正方形的边长均为1个单位长度,△ABC的各顶点都在网格的格点上,若记点A的坐标为(﹣1,3),点C的坐标为(1,﹣1).
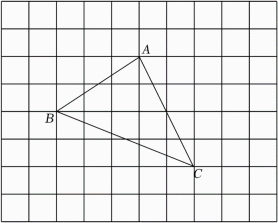 (1)、请在图中建立平面直角坐标系.(2)、写出点B的坐标.(3)、将△ABC先向下平移2个单位长度,再向右平移3个单位长度得到△A'B'C',请画出△A'B'C'.
(1)、请在图中建立平面直角坐标系.(2)、写出点B的坐标.(3)、将△ABC先向下平移2个单位长度,再向右平移3个单位长度得到△A'B'C',请画出△A'B'C'.五、解答题
-
17. 完成下面的证明.
已知:如图, , .
求证: .
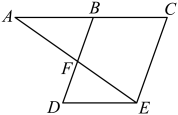
证明:∵( ),
(已知),
∴
∴∥ ▲ (同旁内角互补,两直线平行).
∴ ▲ (两直线平行,同位角相等).
∵(已知),
∴( ),
∴( ).
∴( ).
18. 已知:直线 , 点A和点B是直线a上的点,点C和点D是直线b上的点,连接 , , 设直线和交于点E .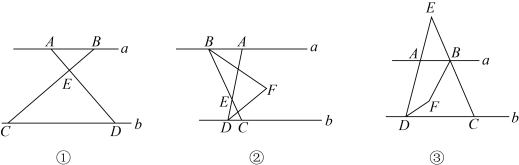 (1)、在如图1所示的情形下,若 , 求的度数;(2)、在如图2所示的情形下,若平分 , 平分 , 且与交于点F , 当 , 时,求的度数;(3)、如图3,当点B在点A的右侧时,若平分 , 平分 , 且 , 交于点F , 设 , , 用含有α , β的代数式表示的补角.19. 已知 , , .(1)、若点在第二象限内,且 , , 求点的坐标,并求的面积;(2)、若点在第四象限内,且的面积为8, , 求点的坐标.
(1)、在如图1所示的情形下,若 , 求的度数;(2)、在如图2所示的情形下,若平分 , 平分 , 且与交于点F , 当 , 时,求的度数;(3)、如图3,当点B在点A的右侧时,若平分 , 平分 , 且 , 交于点F , 设 , , 用含有α , β的代数式表示的补角.19. 已知 , , .(1)、若点在第二象限内,且 , , 求点的坐标,并求的面积;(2)、若点在第四象限内,且的面积为8, , 求点的坐标.六、实践探究题
-
20. 用计算器探究:
将2连续开平方,按键顺序如下:

继续按=……你发现了什么?再用5,14,23,……等大于1的数试一试.
21. 【学习新知】射到平面镜上的光线(入射光线)和反射后的光线(反射光线)与平面镜所夹的角相等.如图1,若入射光线与水平镜面夹角为 , 反射光线与水平镜面夹角为 , 则 . (1)、【初步应用】如图2,有两块平面镜 , , 入射光线经过两次反射,得到反射光线 , 若 , 证明:;(2)、【拓展探究】如图3,有三块平面镜 , , , 入射光线经过三次反射,得到反射光线 , 已知 , , 若要使 , 则为多少度?
(1)、【初步应用】如图2,有两块平面镜 , , 入射光线经过两次反射,得到反射光线 , 若 , 证明:;(2)、【拓展探究】如图3,有三块平面镜 , , , 入射光线经过三次反射,得到反射光线 , 已知 , , 若要使 , 则为多少度?七、综合题
-
22. 如图,AB∥CD,点O是直线AB上一点,OC平分∠AOF.
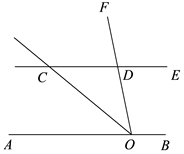 (1)、求证:∠DCO=∠COF;(2)、若∠DCO=40°,求∠EDF的度数.23. 如图,在四边形中, , .
(1)、求证:∠DCO=∠COF;(2)、若∠DCO=40°,求∠EDF的度数.23. 如图,在四边形中, , .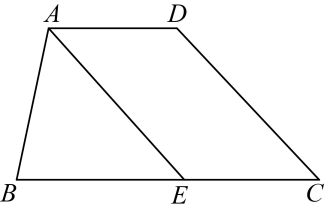 (1)、求的度数;(2)、若平分交于点 , , 请说明与的位置关系.24. 课上老师提出一个问题:“如图,已知 , 于点 , 交于点 , 当时,求的度数.”
(1)、求的度数;(2)、若平分交于点 , , 请说明与的位置关系.24. 课上老师提出一个问题:“如图,已知 , 于点 , 交于点 , 当时,求的度数.”
甲、乙、丙三位同学用不同的方法添加辅助线解决问题如图1,图2,图3所示.
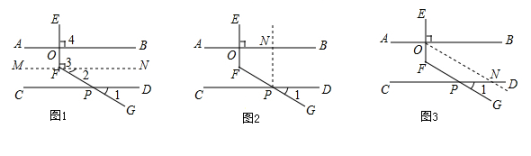 (1)、补全甲同学的分析思路.
(1)、补全甲同学的分析思路.辅助线:过点作 .
分析思路:
①欲求∠EFG的度数,由图可知只需转化为求 ▲ 和 ▲ 的度数之和;
②由辅助线作图可知;
③由 , 推出 ▲ , 由此可推出;
④由已知 , 可得 , 所以可得的度数,从而可求的度数.
(2)、请你根据乙同学所画的辅助线,补全求解过程.解:过作 ▲ , 交于点 .
▲ (两直线平行,同位角相等).
,
,
( ).
∵ .
( ),
,
▲ .
(3)、请你根据丙同学所画的辅助线,求的度数.
-
-