2024年初中数学人教版七年级下学期期中模拟考试卷 04
试卷更新日期:2024-04-16 类型:期中考试
一、单选题
-
1. 象棋在中国有着三千多年的历史,如图是一方的棋盘,如果“帅”的坐标是(1,1),“卒”的坐标是(3,2),那么“马”的坐标是( )
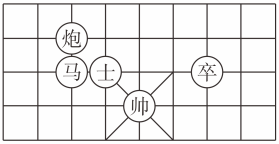 A、 B、 C、 D、2. 如图所示的数轴被墨迹污染了,则下列选项中可能被覆盖住的数是( )
A、 B、 C、 D、2. 如图所示的数轴被墨迹污染了,则下列选项中可能被覆盖住的数是( )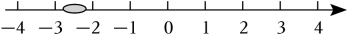 A、 B、﹣ C、﹣ D、﹣3. 估计的值介于( )A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间4. 如图, , , 若点P在直线BC上,则AP的长可能是( )
A、 B、﹣ C、﹣ D、﹣3. 估计的值介于( )A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间4. 如图, , , 若点P在直线BC上,则AP的长可能是( )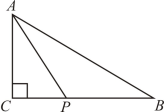 A、4 B、5 C、6 D、75. 如图中的图案哪一个可以看作是由图案自身的一部分平移后得到的( )A、
A、4 B、5 C、6 D、75. 如图中的图案哪一个可以看作是由图案自身的一部分平移后得到的( )A、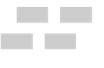 B、
B、 C、
C、 D、
D、 6. 如图, ,直线 分别交 , 于点M,N,将一个含有45°角的直角三角尺按如图所示的方式摆放,若 ,则 等于( )
6. 如图, ,直线 分别交 , 于点M,N,将一个含有45°角的直角三角尺按如图所示的方式摆放,若 ,则 等于( )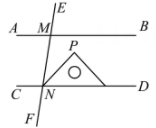 A、15° B、25° C、35° D、45°7. 如图,直线l1与l2相交于点O,点P是平面内任意一点,点P到直线l1的距离为2,且到直线l2的距离为3,则符合条件的点P的个数是( )
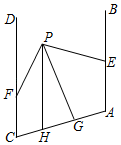
A、15° B、25° C、35° D、45°7. 如图,直线l1与l2相交于点O,点P是平面内任意一点,点P到直线l1的距离为2,且到直线l2的距离为3,则符合条件的点P的个数是( )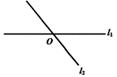 A、2 B、3 C、4 D、无数个8. 如右图,AB∥CD , PG平分∠EPF , ∠A+∠AHP=180°,下列结论:
A、2 B、3 C、4 D、无数个8. 如右图,AB∥CD , PG平分∠EPF , ∠A+∠AHP=180°,下列结论:①CD∥PH;②∠BEP+∠DFP=2∠EPG;③∠FPH=∠GPH;④∠A+∠AGP+∠DFP﹣∠FPG=180°;⑤若∠BEP>∠DFP , 则 =2,
其中正确结论的个数是( )
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
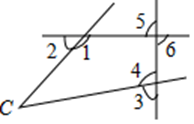
9. 64的算术平方根是 , 的平方根是 .10. 在平面直角坐标系中,点所在的象限是第象限.11. 如图,与 是内错角的是.
 12. 把命题“等边三角形的三个内角都等于60°”写成“如果…那么…”的形式为 .13. 若与的两边分别平行,且比的3倍少24°,则的度数是.14. 将一副三角板如图摆放,已知∠BAC=∠ADE=90°,AE∥BC,则∠DAF的度数是 .
12. 把命题“等边三角形的三个内角都等于60°”写成“如果…那么…”的形式为 .13. 若与的两边分别平行,且比的3倍少24°,则的度数是.14. 将一副三角板如图摆放,已知∠BAC=∠ADE=90°,AE∥BC,则∠DAF的度数是 . 15. 已知∠ABG为锐角,AH∥BG,点C从点B(点C不与点B重合)出发,沿射线BG的方向移动,CD∥AB交直线AH于点D,CE⊥CD交AB于点E,CF⊥AD,垂足为点F(点F不与点A重合).若∠ECF=n°,则∠BAF=.(用n来表示)16. 如图,QP∥MN,A,B分别为直线MN,PQ上两点,且∠BAN=60°,射线AE从AM开始绕点A按顺时针方向旋转至AN后立即回转,然后以不变的速度在AM和AN之间不停地来回旋转,射线BF从BQ绕点B按逆时针方向同时开始旋转,射线AE转动的速度是4°/s,射线BF转动的速度是1°/s,在射线BF到达BP之前,有次射线AE与射线BF互相平行,时间分别是s.
15. 已知∠ABG为锐角,AH∥BG,点C从点B(点C不与点B重合)出发,沿射线BG的方向移动,CD∥AB交直线AH于点D,CE⊥CD交AB于点E,CF⊥AD,垂足为点F(点F不与点A重合).若∠ECF=n°,则∠BAF=.(用n来表示)16. 如图,QP∥MN,A,B分别为直线MN,PQ上两点,且∠BAN=60°,射线AE从AM开始绕点A按顺时针方向旋转至AN后立即回转,然后以不变的速度在AM和AN之间不停地来回旋转,射线BF从BQ绕点B按逆时针方向同时开始旋转,射线AE转动的速度是4°/s,射线BF转动的速度是1°/s,在射线BF到达BP之前,有次射线AE与射线BF互相平行,时间分别是s.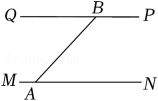
三、计算题
-
17. 计算: .
四、作图题
-
18. 如图,在由边长为个单位长度的正方形组成的网格中,用表示点的位置,用表示点的位置.
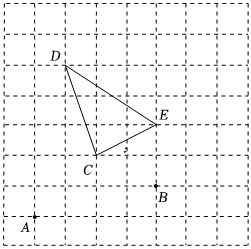 (1)、请画出平面直角坐标系,并写出点的坐标.(2)、请画出向下平移个单位长度,再向右平移个单位长度后的 .
(1)、请画出平面直角坐标系,并写出点的坐标.(2)、请画出向下平移个单位长度,再向右平移个单位长度后的 .五、解答题
-
19. 观察下面三个三角形的形状,找出它们的共同特征,并对有这些共同特征的三角形下一个定义.
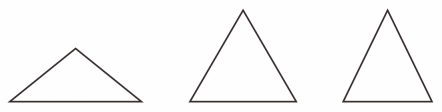 20. 如图(1),AB∥CD,猜想∠BPD与∠B.∠D的关系,说明理由.(提示:三角形的内角和等于180°)
20. 如图(1),AB∥CD,猜想∠BPD与∠B.∠D的关系,说明理由.(提示:三角形的内角和等于180°)①填空或填写理由
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180° ▲
∵AB∥CD,EF∥AB,
∴ ▲ ∥ ▲ , (如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD+ ▲ =180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
②依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B.∠D的关系,并说明理由.
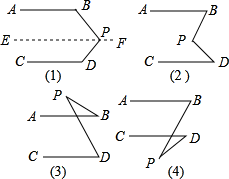
③观察图(3)和(4),已知AB∥CD,直接写出图中的∠BPD与∠B.∠D的关系,不说明理由.
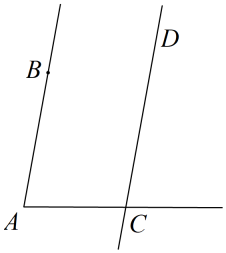
21. 如图,一条街道的两个拐角 , ,这时街道 与 平行吗?为什么?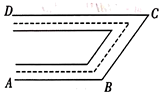
六、实践探究题
-
22. [阅读材料]
∵<< , 即2<<3,
∴1<-1<2.
∴-1的整数部分为1.
∴-1的小数部分为-2.
[解决问题]
(1)、填空: 的小数部分是 .(2)、已知a是 的整数部分,b是 的小数部分,求代数式(-a)3+(b+4)2的值.23. 阅读材料回答问题在平面直角坐标系中,定义,点P沿着水平和竖直方向运动到达点Q的最短路径的长度为P , Q两点之间的“横纵距离”.如图所示,点A的坐标为 , 则A , O两点的“横纵距离”为5.
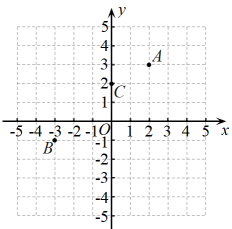
解决问题
(1)、已知点B的坐标为 , 则B , O两点的“横纵距离”为;A , B两点的“横纵距离”为;(2)、已知点C的坐标为 , 写出两个与点C的“横纵距离”为3的点的坐标.(3)、拓展延伸
已知D , O两点的“横纵距离”为5;D , C两点的“横纵距离”为3.请写出满足条件的点D的纵坐标的取值范围.七、综合题
-
24. 如图, .
 (1)、尺规作图:过点B作直线(要求:不写作法,保留作图痕迹);(2)、若 , 点E是直线a上的一点(不与点B重合),则°.25. 直线 , 直线l3、l4分别与l1、l2交于点B、F和A、E,点D是直线l3上一动点,交l4于点C.
(1)、尺规作图:过点B作直线(要求:不写作法,保留作图痕迹);(2)、若 , 点E是直线a上的一点(不与点B重合),则°.25. 直线 , 直线l3、l4分别与l1、l2交于点B、F和A、E,点D是直线l3上一动点,交l4于点C.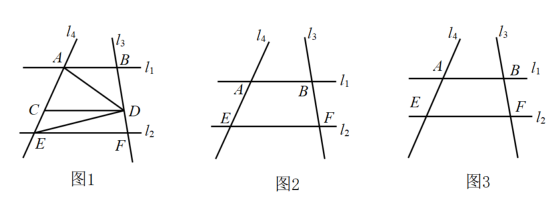 (1)、如图1,当点D在l1、l2两线之间运动时,试找出∠BAD、∠DEF、∠ADE之间的等量关系,并说明理由;(2)、当点D在l1、l2两线外侧运动时,试探索∠BAD、∠DEF、∠ADE之间的等量关系(点D和B、F不重合),画出图形,直接写出结论.26. 阅读理解:如图 , 已知点是外一点,连接 , 求的度数.
(1)、如图1,当点D在l1、l2两线之间运动时,试找出∠BAD、∠DEF、∠ADE之间的等量关系,并说明理由;(2)、当点D在l1、l2两线外侧运动时,试探索∠BAD、∠DEF、∠ADE之间的等量关系(点D和B、F不重合),画出图形,直接写出结论.26. 阅读理解:如图 , 已知点是外一点,连接 , 求的度数.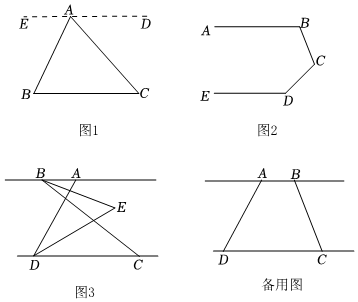 (1)、阅读并补充下面推理过程.
(1)、阅读并补充下面推理过程.解:过点作 , , .
.
.
解题反思:从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将 , , “凑”在一起,得出角之间的关系,使问题得以解决.
(2)、方法运用:如图2,已知 , 求的度数.(3)、深化拓展:如图3,已知 , 点在点的右侧, , 平分 , 点是直线上的一个动点(不与点重合), , 平分 , , 所在的直线交于点 , 点在与两条平行线之间.若 , 请你直接写出的度数.(用含的代数式表示).
-
-