贵州省遵义市2023-2024学年七年级下学期4月月考数学试题

试卷更新日期：2024-04-16 类型：月考试卷

进入出卷网下载

一、选择题（本大题共12小题，每小题3分，共36分）

1. 下列图标中，能通过基本图形平移得到的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各数是无理数的是（）

A、 $- \frac{1}{2}$ B、0 C、 $\sqrt{5}$ D、 $3.1415926$

查看试题解析
3. 如图，将直角三角形的直角顶点放在直尺的一边 $B C$ 上 $(A D ∥ B C)$ ，若 $∠ 1 = 35 °$ ，则 $∠ 2$ 的度数为（）

A、55° B、45° C、40° D、35°

查看试题解析
4. 下列四个实数中，最大的数是（）

A、 $\sqrt{3}$ B、2 C、0 D、 $- 3$

查看试题解析
5. 爱动脑筋的朋朋在学习直线与直线相交所成的角的关系时，他将3根小棒拼成了如图所示的形状，则图中所成的角中，同旁内角的对数有（）

A、0对 B、3对 C、6对 D、12对

查看试题解析
6. 下列选项中，最接近 $\sqrt{6}$ 的整数是（）

A、0 B、1 C、2 D、3

查看试题解析
7. 如图，某村庄要在河岸 $l$ 上建一个水泵房引水到 $C$ 处．他们的做法是：过点 $C$ 作 $C D ⊥ l$ 于点D，将水泵房建在了D处，这样做最节省水管长度，其数学道理是（）

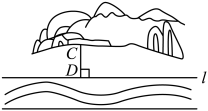A、两点确定一条直线 B、垂线段最短 C、两点之间，线段最短 D、过一点有且仅有一条直线与已知直线垂直

查看试题解析
8. 如图，下列条件中，不能判断直线a∥b的是（）

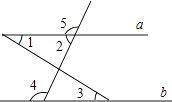A、∠1=∠3 B、∠2+∠4=180° C、∠4=∠5 D、∠2=∠3

查看试题解析
9. 一个正数的两个平方根分别为 $2 m - 1$ 与 $2 - m$ ，则这个正数为（）

A、 $- 1$ B、3 C、4 D、9

查看试题解析
10. 如图，快艇从P处向正北航行到A处时，向左转50°航行到B处，再向右转80°继续航行，此时的航行方向为（）

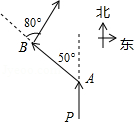A、北偏东30° B、北偏东80° C、北偏西30° D、北偏西50°

查看试题解析
11. 根据表中的信息判断，下列语句正确的是（）
n
256
259.21
262.44
265.69
268.96
272.25
275.56
$\sqrt{n}$
16
16.1
16.2
16.3
16.4
16.5
16.6

A、 $\sqrt{25.921} = 1.61$ B、 $\sqrt{263} < 16.2$ C、只有3个正整数n满足 $16.2 < \sqrt{n} < 16.3$ D、 $\sqrt{2755.6} = 166$

查看试题解析
12. 如图， $A F ∥ C D$ ， $C B$ 平分 $∠ A C D$ ， $B D$ 平分 $∠ E B F$ ，且 $B C ⊥ B D$ ，下列结论：① $B C$ 平分 $∠ A B E$ ；② $A C ∥ B E$ ；③ $∠ C B E + ∠ E D B = 90 °$ ；④ $∠ D E B = 2 ∠ A B C$ .其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（本大题共4个小题，每小题4分，共16分，请把正确答案填写在答题卡相应位置上.）

13. 计算： $\sqrt{4}$ ＝

查看试题解析
14. 用“如果…那么…”的形式将命题“ $\sqrt{3}$ 是无理数”写成.

查看试题解析
15. 如图，每个小正方形的边长为1，把阴影部分剪下来，用剪下来的阴影部分拼成个正方形，那么新正方形的边长是.

查看试题解析
16. 如图， $A B ∥ C D$ ， $E$ 为 $A B$ 上一点，且 $E F ⊥ C D$ 垂足为 $F$ ， $∠ C E D = 90 °$ ， $C E$ 平分 $∠ A E G$ ，且 $∠ C G E = α$ ，则下列结论：
① $∠ E D G = \frac{1}{2} α$ ；② $∠ C E B = 2 α$ ；③ $∠ C E F = 90 ° - \frac{α}{2}$ ；④ $∠ F E D + ∠ D C E = 180 ° - α$ ；
其中正确的有.（请填写序号）

查看试题解析

三、解答题（本大题共9小题，共98分，解答要写出必要的文字说明、证明过程或演算步骤）

17. 计算：

(1)、 $- 1^{2024} + \sqrt[3]{27} + | - \sqrt{3} | - \sqrt{16}$ ；

(2)、 $2 \sqrt{3} (\sqrt{3} - \frac{1}{\sqrt{3}})$ .

查看试题解析
18. 求满足下列各式的未知数 $x$ .

(1)、 $27 x^{3} + 125 = 0$ ；

(2)、 ${(x + 2)}^{2} = 16$ .

查看试题解析
19. 如图，每个小正方形的边长都为1，三角形 $A B C$ 的顶点都在格点上（每个小正方形的顶点叫格点）.

(1)、平移三角形 $A B C$ ，使点 $A$ 平移到点 $D$ （点 $B$ 平移到点 $E$ ，点 $C$ 平移到点 $F$ ），画出平移后的三角形 $D E F$ ；

(2)、连接 $B E$ ， $B F$ ，求三角形 $B E F$ 的面积.

查看试题解析
20. 已知 $2 a - 1$ 的算术平方根是3， $3 a + b - 9$ 的立方根是2， $c$ 是 $\sqrt{13}$ 的整数部分，求 $2 a + b - c^{2}$ 的平方根.

查看试题解析
21. 过程填空：
如图， $A B$ 和 $C D$ 交于点 $O$ ， $∠ C = ∠ C O A$ ， $∠ D = ∠ B O D$ ，过点 $O$ 作 $O M ⊥ B D$ 于点 $M$ ，延长 $M O$ 交 $A C$ 于点 $N$ ，求证： $O N ⊥ A C$ .
证明：
证明：∵_▲_（已知），
∴ $∠ O M B = 90 °$ （_▲_）.
∵ $∠ C = ∠ C O A$ ， $∠ D = ∠ B O D$ （_▲_），
又∵ $∠ C O A = ∠ B O D$ （_▲_），
∴ $∠ C =$ _▲_（_▲_）.
∴_▲_ $∥ A C$ （_▲_）.
∴_▲_ $= ∠ O M B$ （_▲_）.
∴ $∠ O N A = 90 °$ .
∴ $O N ⊥ A C$ .

查看试题解析
22. 某市在招商引资期间，把已倒闭的机床厂租给外地某投资商，该投资商为减小固定资产投资，将原有的正方形场地改建成800平方米的长方形场地，且其长、宽的比为 $5 : 2$ .

(1)、求改建后的长方形场地的长和宽为多少米？

(2)、如果把原来面积为900平方米的正方形场地的金属栅栏围墙全部利用，来作为新场地的长方形围墙，栅栏围墙是否够用？为什么？

查看试题解析
23. 如图，点 $O$ 在直线 $A B$ 上， $∠ B O C = 40 °$ ，射线 $O D$ 在 $∠ B O C$ 内部.

图1 图2

(1)、如图1，当 $∠ B O D = ∠ C O D$ 时，用量角器画出射线 $O D$ ，则 $∠ A O D$ 度数为°；

(2)、如图2，当 $∠ B O D = α$ 时， $O E ⊥ O D$ ，垂足为点 $O$ ，求 $∠ A O E$ 度数（用含 $α$ 的式子表示）.

查看试题解析
24. 阅读材料：
我们定义：如果一个数的平方等于 $- 1$ ，记作 $i^{2} = - 1$ ，那么这个i就叫做虚数单位，虚数与我们学过的实数结合在一起叫做复数，一个复数可以表示为 $a + b i$ （ $a$ ， $b$ 均为实数）的形式，其中 $a$ 叫做它的实部， $b$ 叫做它的虚部.
复数的加、减、乘的运算与我们学过的整式加、减、乘的运算类似.
例如：计算 $(5 + i) + (3 - 4 i) = (5 + 3) + (i - 4 i) = 8 - 3 i$ .
根据上述材料，解决下列问题：

(1)、填空： $i^{3} =$ ， $i^{4} =$ ；

(2)、计算： $(6 - 5 i) + (- 3 + 7 i)$ ；

(3)、计算： $3 (2 - 6 i) - 4 i (5 - i)$ .

查看试题解析
25. 【学习新知】
射到平面镜上的光线（入射光线）和反射后的光线（反射光线）与平面镜所夹的角相等.如图1， $A B$ 是平面镜，若入射光线与水平镜面的夹角为 $∠ 1$ ，反射光线与水平镜面的夹角为 $∠ 2$ ，则 $∠ 1 = ∠ 2$ .
【初步应用】
生活中我们可以运用“激光”和两块相交的平面镜进行测距，如图2当一束“激光” $D O_{1}$ 射到平面镜 $A B$ 上，被平面镜 $A B$ 反射到平面镜 $B C$ 上，又被平面镜 $B C$ 反射后得到反射光线 $O_{2} E$ ，回答下列问题：
图1 图2 图3

(1)、当 $D O_{1} ∥ E O_{2}$ ， $∠ A O_{1} D = 30 °$ （即 $∠ 1 = 30 °$ ）时，求 $∠ O_{1} O_{2} E$ 的度数；

(2)、当 $∠ B = 90 °$ 时，任何射到平面镜 $A B$ 上的光线 $D O_{1}$ 经过平面镜 $A B$ 和 $B C$ 的两次反射后，入射光线与反射光线总是平行的.请你根据所学知识及新知说明理由；
（提示：三角形的内角和等于180°）

(3)、【拓展探究】如图3，有三块平面镜 $A B$ ， $B C$ ， $C D$ ，入射光线 $E O_{1}$ 经过三次反射，得到反射光线 $O_{3} F$ ，已知 $∠ 1 = ∠ 6 = 35 °$ ，若要使 $E O_{1} ∥ O_{3} F$ ，请直接写出 $∠ B$ 的度数.

查看试题解析

n	256	259.21	262.44	265.69	268.96	272.25	275.56
$\sqrt{n}$	16	16.1	16.2	16.3	16.4	16.5	16.6