2024年人教版初中数学七年级下学期期中重难点训练 01 平行线

试卷更新日期：2024-04-16 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，直线AB，CD相交于点 $O$ .若 $∠ 1 = 8 0^{°} ， ∠ 2 = 3 0^{°}$ ，则 $∠ A O E$ 的度数为（）

A、 $3 0^{°}$ B、 $5 0^{°}$ C、 $6 0^{°}$ D、 $8 0^{°}$

查看试题解析
2. 如图，计划把河水l引到水池A中，先作AB⊥l ，垂足为B ，然后沿AB开渠，能使所开的渠道最短，这样设计的依据是（　　）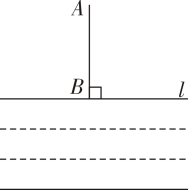

A、两点之间线段最短 B、垂线段最短 C、过一点只能作一条直线 D、平面内，过一点有且只有一条直线与已知直线垂直

查看试题解析
3. 传统文化风筝是由中国古代劳动人民发明于东周春秋时期的产物，其材质在不断改进之后，坊间开始用纸做风筝，称为“纸鸢”．如图所示的纸骨架中，与 $∠ 3$ 构成同旁内角的是（　　）

A、 $∠ 1$ B、 $∠ 2$ C、 $∠ 4$ D、 $∠ 5$

查看试题解析
4. 如图，小丽的奶奶家在A点的正北方向C处，但需要走一条弯的路才能到达，小丽先沿北偏东 $57 °$ 走了一段距离后，转弯沿北偏西 $33 °$ 再走一段距离即可走到奶奶家，则转弯处∠ABC的度数为（　　）

A、 $33 °$ B、 $57 °$ C、 $90 °$ D、 $100 °$

查看试题解析
5. 运动会上，跳远运动员跳落到沙坑时的痕迹和测量跳远成绩的方法如图所示，选择其中的③号线的长度作为跳远成绩，这样测量的依据是（）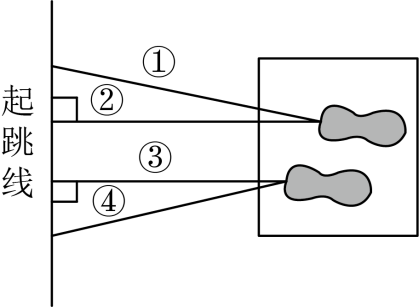

A、两点之间，线段最短 B、垂线段最短 C、两点确定一条直线 D、平行线之间的距离处处相等

查看试题解析
6. 如图，街道 $A B$ 与 $C D$ 平行，拐角 $∠ A B C = 136 °$ ，则拐角 $∠ B C D$ 的度数是（）

A、 $44 °$ B、 $54 °$ C、 $106 °$ D、 $136 °$

查看试题解析
7. 如图，点 $E$ 在线段BC的延长线上，下列四个结论中正确的个数是（）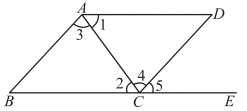
①如果 $∠ 3 = ∠ 4$ ，那么 $A D / / B C$
②如果 $∠ 1 = ∠ 2$ ，那么 $A D / / B C$
③如果 $A D / / B C$ ，那么 $∠ D + ∠ B C D = 18 0^{°}$
④如果 $A B / / D C$ ，那么 $∠ B = ∠ 5$

A、1 B、2 C、3 D、4

查看试题解析
8. 如图，直线 $A B, C D$ 被直线 $C E$ 所截， $A B ∥ C D, ∠ 1 = 140 °$ ，则 $∠ C$ 的度数为（）

A、 $30 °$ B、 $40 °$ C、 $50 °$ D、 $60 °$

查看试题解析
9. 如图， $A C ⊥ B C$ ， $C D ⊥ A B$ ，垂足分别为 $C, D$ ．下列说法正确的个数是（）
①点 $C$ 到线段 $A B$ 的距离为线段 $C D$ 的长度；
② $∠ A C D + ∠ B = 9 0^{∘}$ ；
③ $∠ A = ∠ B C D$ ；
④将三角形 $A B C$ 绕线段 $B C$ 所在直线旋转一周得到的几何体是圆锥．

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，烧杯内液体表面 $A B$ 与烧杯下底部 $C D$ 平行，光线 $E F$ 从液体中射向空气时发生折射，光线变成 $F H$ ，点 $G$ 在射线 $E F$ 上．已知 $∠ H F B = 20 °$ ， $∠ F E D = 60 °$ ，则 $∠ G F H$ 的度数为（）

A、 $20 °$ B、 $40 °$ C、 $60 °$ D、 $80 °$

查看试题解析

二、填空题

11. 如图，计划把河水引到水池A中，先作 $A B ⊥ C D$ ，垂足为B，然后沿 $A B$ 开渠，能使所开的渠道最短，这样设计的依据是．

查看试题解析
12. 如图， $A B / / C D$ ， $B C / / D E$ ， $∠ B = 72 °$ ，则 $∠ D =$ 度．

查看试题解析
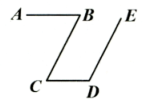13. 如图，在一块长为 $10 m$ ，宽为 $7 m$ 的长方形草地上，有一条路宽为 $1 m$ 的小路，这块草地的绿地面积为 $m^{2}$ ．

查看试题解析
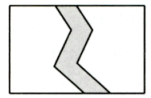14. 如图为一盏可折叠台灯及其平面示意图，其中支架 $A O$ 与底座 $O E$ 垂直，支架 $A B$ ， $B C$ 为固定支撑杆，当灯体 $C D$ 与底座 $O E$ 平行时， $∠ B A O = 138 °$ ， $∠ B C D = 154 °$ ，则 $∠ B$ 的度数为 $°$ ．

查看试题解析
15. 如图，平行于主光轴 $M N$ 的光线 $A B$ 和 $C D$ 经过凹透镜的折射后，折射光线 $B E$ ， $D F$ 的反向延长线交于主光轴 $M N$ 上一点P.若 $∠ A B E = 150 °$ ， $∠ C D F = 160 °$ ，则 $∠ E P F$ 的度数是.

查看试题解析
16. 如图1，在探索“如何过直线外一点作已知直线的平行线”时，小颖利用两块完全相同的三角尺进行如下操作：如图 2 所示，（1）用第一块三角尺的一条边贴住直线 l，第二块三角尺的一条边紧靠第一块三角尺；（2）将第二块三角尺沿第一块三角尺移动，使其另一边经过点 A，沿这边作出直线 AB，直线 AB 即为所求，则小颖的作图依据是．

查看试题解析

三、解答题

17. 如图，直线 $A B$ ， $C D$ 与 $E F$ 交于M ， N两点， $∠ 1 = ∠ 2$ ，且 $M Q$ 平分 $∠ E M B$ ， $N P$ 平分 $∠ M N D$ ，求证：直线 $A B ∥ C D$ ．

查看试题解析
18. 如图，直线 $E F$ 与 $C D$ 交于点O ， $O A$ 平分 $∠ C O E$ 交直线l于点A ， $O B$ 平分 $∠ D O E$ 交直线l于点B ，且 $∠ 1 + ∠ 2 = 90 °$ ．

(1)、求 $∠ A O B$ 的度数：

(2)、求证： $A B ∥ C D$ ；

(3)、若 $∠ 2 ： ∠ 3 = 2 ： 5$ ，求 $∠ A O F$ 的度数．

查看试题解析
19. 如图，点B、 O、 C三点在同一直线上， $∠ D O E = 90 °$ ，

(1)、若 $A O ⊥ B C ， ∠ A O E = 65 °$ ，求 $∠ C O E$ 的度数；

(2)、若 $∠ B O D ： ∠ C O E = 2 ： 1$ ，求 $∠ C O D$ 的度数．

查看试题解析

四、实践探究题

20. 如图是一个“跳棋”棋盘，其游戏规则是：一个棋子从某一个起始角开始，经过若干步跳动以后，到达终点角，跳动时，每一步只能跳到它的同位角或内错角或同旁内角的位置上.
例如，从起始角∠1跳到终点角∠3，有两种不同的路径：①∠1，∠9，∠3；②∠1，∠12，∠6，∠10，∠3.
问：从起始角∠1 依次按同位角、内错角、同旁内角的顺序跳，能否跳到终点角∠8? 若能，请写出路径；若不能，请说明理由.

查看试题解析
21. 如图，已知OC平分∠AOB，CD⊥OA于点D，E为DC延长线上一点，EF⊥OB于点F，EG平分∠DEF交OB于点G，∠DEF+∠AOB＝180°.

(1)、问题发现：①如图1，当∠AOB＝90°时，∠1+∠2= ▲ °；
②如图2，当∠AOB为锐角时，∠1与∠2有什么数量关系，请说明理由；

(2)、拓展探究：（3）在（2）的条件下，已知直角三角形中两个锐角的和是90°，试探究OC与GE的位置关系，并证明结论．

查看试题解析

五、综合题

22. 如图，已知直线AB∥DF，∠D+∠B=180°，

(1)、求证：DE∥BC；

(2)、如果∠AMD=75°，求∠AGC的度数．

查看试题解析
23. 如图，已知 $A M ∥ B N$ ， $∠ A = 60 °$ ．点P是射线AM上一动点（与点A不重合）、BC ， BD分别平分 $∠ A B P$ 和 $∠ P B N$ ，分别交射线AM于点C ， D ．

(1)、求 $∠ C B D$ 的度数．

(2)、当点P运动到使 $∠ A C B = ∠ A B D$ 时， $∠ A B C$ 的度数是多少？为什么？

(3)、当点P运动时， $∠ A P B$ 与 $∠ A D B$ 之间的数量关系是否随之发生变化？若不变化．请写出它们之间的关系，并说明理由；若变化，请写出变化规律．

查看试题解析