四川省绵阳市江油市八校联考2022-2023学年九年级下学期3月月考数学试题
试卷更新日期:2024-04-16 类型:月考试卷
一、选择题:本大题共12个小题,每小题3分,共36分.每个小题只有一个选项符合题目要求
-
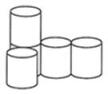
1. 若|5﹣x|=x﹣5,则x的取值范围为( )A、x>5 B、x≥5 C、x<5 D、x≤52. 如图是由5个高度相等大小相同的圆柱搭成的几何体,从左边看是( )
 A、
A、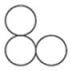 B、
B、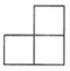 C、
C、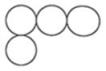 D、
D、 3. 党的二十大报告中指出,我国全社会研发经费支出从一万亿元增加到二万八千亿元,居世界第二位,研发人员总量居世界首位.将2800000000000用科学记数法表示为( )A、0.28×1013 B、2.8×1011 C、2.8×1012 D、28×10114. 关于等边三角形,下列说法不正确的是( )A、等边三角形是轴对称图形 B、所有的等边三角形都相似 C、等边三角形是正多边形 D、等边三角形是中心对称图形5. 对某村一到六年级适龄儿童人数进行了统计,得到每个年级的儿童人数分别10,15,10,17,18,20.对于这组数据,下列说法错误的是( )A、平均数是15 B、众数是10 C、中位数是17 D、方差是6. 如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A(0,a)、B(﹣3,2)、C(c , m)、D(d , m),则点E的坐标是( )
3. 党的二十大报告中指出,我国全社会研发经费支出从一万亿元增加到二万八千亿元,居世界第二位,研发人员总量居世界首位.将2800000000000用科学记数法表示为( )A、0.28×1013 B、2.8×1011 C、2.8×1012 D、28×10114. 关于等边三角形,下列说法不正确的是( )A、等边三角形是轴对称图形 B、所有的等边三角形都相似 C、等边三角形是正多边形 D、等边三角形是中心对称图形5. 对某村一到六年级适龄儿童人数进行了统计,得到每个年级的儿童人数分别10,15,10,17,18,20.对于这组数据,下列说法错误的是( )A、平均数是15 B、众数是10 C、中位数是17 D、方差是6. 如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A(0,a)、B(﹣3,2)、C(c , m)、D(d , m),则点E的坐标是( ) A、(2,﹣3) B、(2,3) C、(3,﹣2) D、(3,2)7. 估算 的值应在( )A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间8. 小明、小颖和小凡都想去影院看电影,但现在只有一张门票,三人决定一起做游戏,谁获胜谁就去,游戏规则是:连续掷两枚质地均匀的硬币,若两枚正面朝上,则小明获胜,若两枚反面朝上,则小颖获胜;若一枚正面朝上,一枚反面朝上,则小凡获胜,关于这个游戏,下列判断正确的是( )A、三人获胜的概率相同 B、小明获胜的概率大 C、小颖获胜的概率大 D、小凡获胜的概率大9. 等底、等体积的圆柱和圆锥,圆锥的高是6分米,圆柱的高是( )。A、2分米 B、3分米 C、6分米 D、18分米10. 如图1,在菱形ABCD中,∠A=60°,动点P从点A出发,沿折线AD→DC→CB方向匀速运动,运动到点B停止.设点P的运动路程为x,△APB的面积为y,y与x的函数图象如图2所示,则AB的长为( )
A、(2,﹣3) B、(2,3) C、(3,﹣2) D、(3,2)7. 估算 的值应在( )A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间8. 小明、小颖和小凡都想去影院看电影,但现在只有一张门票,三人决定一起做游戏,谁获胜谁就去,游戏规则是:连续掷两枚质地均匀的硬币,若两枚正面朝上,则小明获胜,若两枚反面朝上,则小颖获胜;若一枚正面朝上,一枚反面朝上,则小凡获胜,关于这个游戏,下列判断正确的是( )A、三人获胜的概率相同 B、小明获胜的概率大 C、小颖获胜的概率大 D、小凡获胜的概率大9. 等底、等体积的圆柱和圆锥,圆锥的高是6分米,圆柱的高是( )。A、2分米 B、3分米 C、6分米 D、18分米10. 如图1,在菱形ABCD中,∠A=60°,动点P从点A出发,沿折线AD→DC→CB方向匀速运动,运动到点B停止.设点P的运动路程为x,△APB的面积为y,y与x的函数图象如图2所示,则AB的长为( )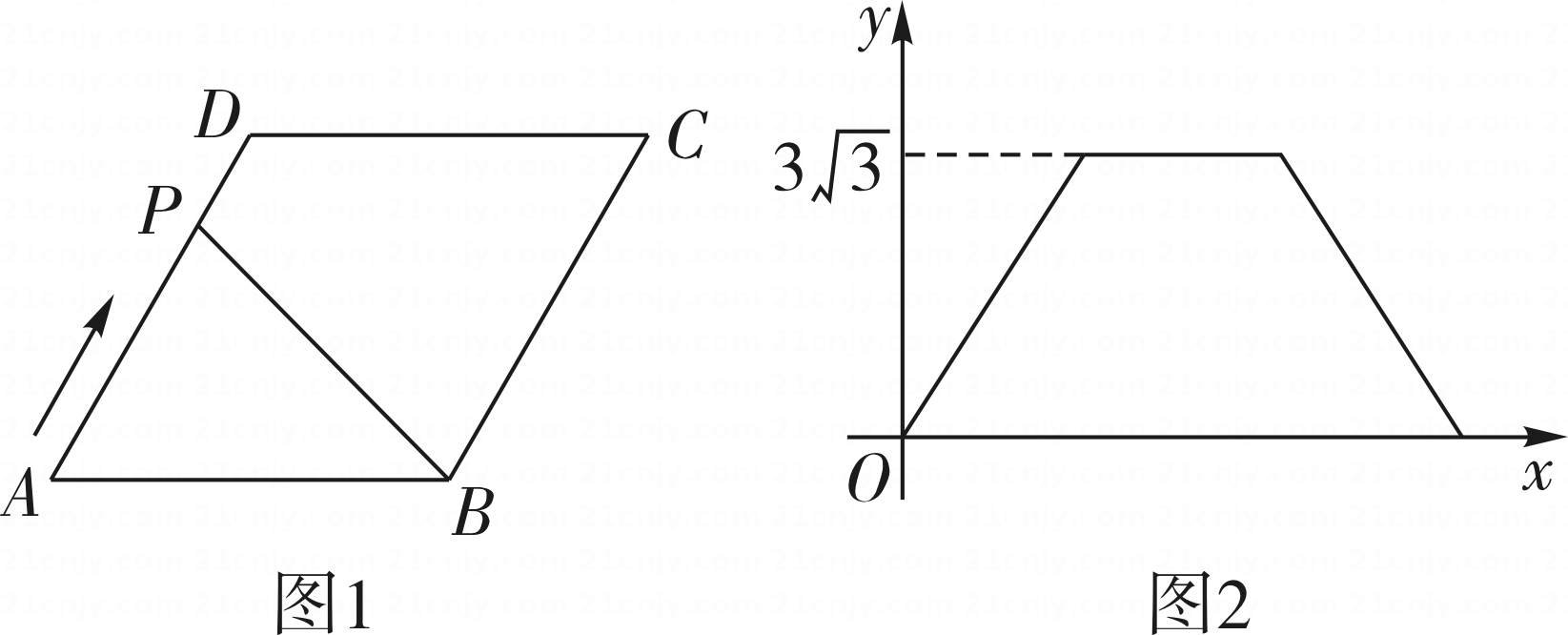 A、 B、2 C、3 D、411. 若抛物线y=x2+x+m﹣1(m是常数)经过第一、二、三象限,则m的取值范围是( )A、m>1 B、m< C、1<m< D、1≤m<12. 如图,在矩形ABCD中,AB=4,AD=6,点P在AD上,点Q在BC上,且AP = CQ,连接CP,QD,则PC + QD的最小值为( )
A、 B、2 C、3 D、411. 若抛物线y=x2+x+m﹣1(m是常数)经过第一、二、三象限,则m的取值范围是( )A、m>1 B、m< C、1<m< D、1≤m<12. 如图,在矩形ABCD中,AB=4,AD=6,点P在AD上,点Q在BC上,且AP = CQ,连接CP,QD,则PC + QD的最小值为( ) A、8 B、10 C、12 D、20
A、8 B、10 C、12 D、20二、填空题:本大题共6个小题,每小题4分,共24分.将答案填写在答题卡相应的横线上.
-
13. 分解因式a3﹣81a的结果是 .14. 若代数式 的值是 , 则x= .15. 如图,在△ABC中,∠A=60°,∠B=40°,DE∥BC,则∠AED的度数为 .
 16. 如图,河岸AD,BC互相平行,桥AB垂直于两岸,从C处看桥的两端A,B,夹角∠BCA=60°,测得BC=14m,则桥长AB=m(结果精确到1m).
16. 如图,河岸AD,BC互相平行,桥AB垂直于两岸,从C处看桥的两端A,B,夹角∠BCA=60°,测得BC=14m,则桥长AB=m(结果精确到1m).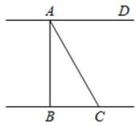 17. 不等式组的解集是 .18. 如图,在△ABC中,∠ACB=90°,点D在AB边上,AD=AC,点E在BC边上,∠BAE=∠ABC,点F为AE上一点,∠ADF=2∠BCD,若DF=2,BD=1,则AD的长为 .
17. 不等式组的解集是 .18. 如图,在△ABC中,∠ACB=90°,点D在AB边上,AD=AC,点E在BC边上,∠BAE=∠ABC,点F为AE上一点,∠ADF=2∠BCD,若DF=2,BD=1,则AD的长为 .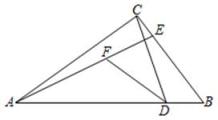
三、解答题:本大题共7个小题,共90分.解答应写出文字说明、证明过程或演算步骤.
-
19.(1)、计算:(﹣2)0+- .(2)、请你先化简( -) , 再从0,﹣2,2,1中选择一个合适的数代入,求出这个代数式的值.20. 在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数分布直方图的高度比为1:5.
月信息消费额分组统计表
组别
消费额(元)
A
10≤x<100
B
100≤x<200
C
200≤x<300
D
300≤x<400
E
x≥400

请结合图表中相关数据解答下列问题:
(1)、这次接受调查的有户;(2)、在扇形统计图中,“E”所对应的圆心角的度数是;(3)、请你补全频数分布直方图;(4)、若该社区有2000户住户,请估计月信息消费额不少于200元的户数是多少?21. 为配合崇明“花博会”,花农黄老伯培育了甲、乙两种花木各若干株.如果培育甲、乙两种花木各一株,那么共需成本500元;如果培育甲种花木3株和乙种花木2株,那么共需成本1200元.(1)、求甲、乙两种花木每株的培育成本分别为多少元?(2)、市场调查显示,甲种花木的市场售价为每株300元,乙种花木的市场售价为每株500元.黄老伯决定在将成本控制在不超过30000元的前提下培育两种花木,并使总利润不少于18000元.若黄老伯培育的乙种花木的数量比甲种花木的数量的3倍少10株,请问黄老伯应该培育甲、乙两种花木各多少株?22. 如图,在平面直角坐标系中,直线y=ax+b与双曲线y= 相交于A(1,m),B(n , ﹣2)两点,直线与x轴、y轴交于C , D两点,且tan∠AOC=1. (1)、求k , a , b的值;(2)、求△AOB的面积.23. 如图,已知:在△ABC中,∠C=90°,点P是BC边上的动点,PD⊥BC交AB于D,以PD为直径的⊙O分别交AB,AP于点E,F.
(1)、求k , a , b的值;(2)、求△AOB的面积.23. 如图,已知:在△ABC中,∠C=90°,点P是BC边上的动点,PD⊥BC交AB于D,以PD为直径的⊙O分别交AB,AP于点E,F. (1)、求证:∠EFP=∠EPB.(2)、若AB=20,sinB= .
(1)、求证:∠EFP=∠EPB.(2)、若AB=20,sinB= .①当∠APB=4∠APD,求PC的长.
②当△PEF为等腰三角形时,请求出所有满足条件的△PEF的腰长.
(3)、若sinB= , 且D,F,C在一条直线上,则DP与AC的比值为 .24. 如图,在平面直角坐标系中,抛物线y=﹣x2﹣2x+c(c为常数)与一次函数y=﹣x+b(b为常数)交于A、B两点,其中A点坐标为(﹣3,0). (1)、求B点坐标;(2)、点P为直线AB上方抛物线上一点,连接PA , PB , 当S△PAB=时,求点P的坐标;(3)、将抛物线y=﹣x2﹣2x+c(c为常数)沿射线AB平移5个单位,平移后的抛物线y1与原抛物线y=﹣x2﹣2x+c相交于点E , 点F为抛物线y1的顶点,点M为y轴上一点,在平面直角坐标系中是否存在点N , 使得以点E , F , M , N为顶点的四边形是菱形,若存在,请直接写出点N的坐标;若不存在,请说明理由.25. 定义:我们把一组对边平行另一组对边相等且不平行的四边形叫做等腰梯形.
(1)、求B点坐标;(2)、点P为直线AB上方抛物线上一点,连接PA , PB , 当S△PAB=时,求点P的坐标;(3)、将抛物线y=﹣x2﹣2x+c(c为常数)沿射线AB平移5个单位,平移后的抛物线y1与原抛物线y=﹣x2﹣2x+c相交于点E , 点F为抛物线y1的顶点,点M为y轴上一点,在平面直角坐标系中是否存在点N , 使得以点E , F , M , N为顶点的四边形是菱形,若存在,请直接写出点N的坐标;若不存在,请说明理由.25. 定义:我们把一组对边平行另一组对边相等且不平行的四边形叫做等腰梯形.
【性质初探】如图1,已知,▱ABCD,∠B=80°,点E是边AD上一点,连结CE,四边形ABCE恰为等腰梯形.求∠BCE的度数;
【性质再探】如图2,已知四边形ABCD是矩形,以BC为一边作等腰梯形BCEF,BF=CE,连结BE、CF.求证:BE=CF;
【拓展应用】如图3,▱ABCD的对角线AC、BD交于点O,AB=2,∠ABC=45°,过点O作AC的垂线交BC的延长线于点G,连结DG.若∠CDG=90°,求BC的长.