四川省绵阳市江油市八校联考2023-2024学年七年级下学期数学月考考试试卷(4月)
试卷更新日期:2024-04-16 类型:月考试卷
一、选择题(每小题3分,共36小题)
-
1. 下列说法中正确的是( )A、4的平方根是2 B、平方根是它本身的数只有0 C、﹣8没有立方根 D、立方根是它本身的数只有0和12. 泰勒斯被誉为古希腊及西方第一个自然科学家和哲学家,据说“两条直线相交,对顶角相等”就是泰勒斯首次发现并论证的.论证“对顶角相等”使用的依据是( )A、等角的补角相等 B、同角的余角相等 C、等角的余角相等 D、同角的补角相等3. 在同一平面内,若a∥b , a∥c , 则b与c的关系为( )A、平行或重合 B、平行或垂直 C、垂直 D、相交4. 根据语句“直线a与直线b相交,点M在直线a上,直线b不经过点M . ”画出的图形正确的是( )A、
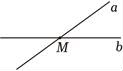 B、
B、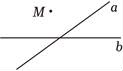 C、
C、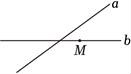 D、
D、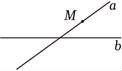 5. 如图,点E在AC的延长线上,下列条件能判断AB∥CD的是( )
5. 如图,点E在AC的延长线上,下列条件能判断AB∥CD的是( ) A、∠1=∠2 B、∠3=∠4 C、∠D=∠DCE D、∠D+∠ACD=180°6. 如图,在下列给出的条件中,不能判定AC∥DF的是( )
A、∠1=∠2 B、∠3=∠4 C、∠D=∠DCE D、∠D+∠ACD=180°6. 如图,在下列给出的条件中,不能判定AC∥DF的是( ) A、∠1=∠2 B、∠4+∠2=180° C、∠2=∠3 D、∠A=∠17. 如图,直线AB , CD被直线CE所截,AB∥CD , ∠1=140°,则∠C的度数为( )
A、∠1=∠2 B、∠4+∠2=180° C、∠2=∠3 D、∠A=∠17. 如图,直线AB , CD被直线CE所截,AB∥CD , ∠1=140°,则∠C的度数为( ) A、30° B、40° C、50° D、60°8. 若2m﹣4与3m﹣1是同一个数两个不同的平方根,则m的值( )A、﹣3 B、1 C、﹣3或1 D、﹣19. 9的平方根是( )A、3 B、﹣3 C、±3 D、10. ﹣8的立方根是( )A、4 B、2 C、﹣2 D、±211. 如图所示,已知直线a∥b , ∠1=120°,∠2=62°,则∠3的度数为( )
A、30° B、40° C、50° D、60°8. 若2m﹣4与3m﹣1是同一个数两个不同的平方根,则m的值( )A、﹣3 B、1 C、﹣3或1 D、﹣19. 9的平方根是( )A、3 B、﹣3 C、±3 D、10. ﹣8的立方根是( )A、4 B、2 C、﹣2 D、±211. 如图所示,已知直线a∥b , ∠1=120°,∠2=62°,则∠3的度数为( ) A、58° B、59° C、60° D、62°12. 如图1,从一个边长为4的正方形纸片扣掉两个边长为a的正方形得到如2图示的图形,若图2周长为22,则a的值是( )
A、58° B、59° C、60° D、62°12. 如图1,从一个边长为4的正方形纸片扣掉两个边长为a的正方形得到如2图示的图形,若图2周长为22,则a的值是( ) A、1 B、1.5 C、2 D、3
A、1 B、1.5 C、2 D、3二、填空题(每空3分,共18分)
-
13. 64的算术平方根是.14. 若实数m , n满足+|n+2|=0,则m+n的值为 .15. 如图,直线l表示一段河道,点P表示村庄,现要从河l向村庄P引水,图中有四种方案,其中沿线段PC路线开挖的水渠长最短,理由是 .
 16. 如图,直线a , b被直线l所截,∠1=60°,∠2=120°.求证:a∥b . 下面是某同学的证明过程,则①为 .
16. 如图,直线a , b被直线l所截,∠1=60°,∠2=120°.求证:a∥b . 下面是某同学的证明过程,则①为 .
证明:∵∠1=60°,
∴∠1=∠3=60°(对顶角相等).
∵∠2=120°,
∴∠2+∠3=120°+60°=180°.
∴a∥b(①).
17. 如图,平行于主光轴MN的光线AB和CD经过凹透镜的折射后,折射光线BE , DF的反向延长线交于主光轴MN上一点P . 若∠ABE=150°,∠CDF=160°,则∠EPF的度数是 . 18. 如图所示,某商场重新装修后,准备在门前台阶上铺设地毯,已知这种地毯的批发价为每平方米40元,其台阶的尺寸如图所示,则购买地毯至少需要元.
18. 如图所示,某商场重新装修后,准备在门前台阶上铺设地毯,已知这种地毯的批发价为每平方米40元,其台阶的尺寸如图所示,则购买地毯至少需要元.
三、解答题(共46分)
-
19. 求下列各式中的x:(1)、4x2=1;(2)、(x﹣1)2﹣27=0.20. 已知x=1﹣2a , y=3a﹣4.(1)、已知x的算术平方根为3,求a的值;(2)、如果一个正数的平方根分别为x , y , 求这个正数.21. 已知:如图,AE与BD相交于点F , ∠B=∠C , ∠1=∠2.求证:AB∥CE .
 22. 在如图所示的平面直角坐标系中,已知点A(1,2),B(3,1).
22. 在如图所示的平面直角坐标系中,已知点A(1,2),B(3,1). (1)、C点的坐标为;(2)、将三角形ABC先向下平移4个单位,在向左平移3个单位,它的像是三角形A1B1C1 , 画出三角形A1B1C1;(3)、三角形A1B1C1的面积为 .23. 如图,已知直线AB、CD相交于点O , OE平分∠AOD , 射线OF在∠BOD内部.
(1)、C点的坐标为;(2)、将三角形ABC先向下平移4个单位,在向左平移3个单位,它的像是三角形A1B1C1 , 画出三角形A1B1C1;(3)、三角形A1B1C1的面积为 .23. 如图,已知直线AB、CD相交于点O , OE平分∠AOD , 射线OF在∠BOD内部. (1)、若∠AOC=56°,求∠DOE的度数;(2)、若∠EOD:∠FOD:∠FOB=7:3:1,求∠COE的度数.
(1)、若∠AOC=56°,求∠DOE的度数;(2)、若∠EOD:∠FOD:∠FOB=7:3:1,求∠COE的度数.

