云南省文山州文山市2023-2024学年八年级上学期期末数学试卷

试卷更新日期：2024-04-16 类型：期末考试

进入出卷网下载

一、选择题（本大题共12小题，每小题只有一个正确选项，每小题3分，满分36分）

1. 下列四组线段中，可以构成直角三角形的是（　　）

A、4cm、5cm、6cm B、6cm、8cm、9cm C、2cm、3cm、4cm D、5cm、12cm、13cm

查看试题解析
2. 下列实数是无理数的是（　　）

A、﹣2 B、1 C、 $\sqrt{2}$ D、2

查看试题解析
3. 如图，笑脸盖住的点的坐标可能为（　　）

A、（2，3） B、（﹣2，3） C、（﹣2，﹣3） D、（2，﹣3）

查看试题解析
4. 如图，AB∥CD ， ∠CEF＝85°，则∠A的度数是（　　）

A、85° B、95° C、105° D、115°

查看试题解析
5. 如表记录了数学兴趣小组甲、乙、丙、丁四名同学最近几次拓展训练的数学成绩，现要选拔一名成绩好且发挥稳定的同学参加比赛，应推选（　　）

甲
乙
丙
丁
平均数
95
96
96
95
方差
2.5
2.4
2.3
2.5

A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 下列计算正确的是（　　）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $3 \sqrt{2} - \sqrt{2} = 2$ C、 $\sqrt{9} = \pm 3$ D、 $\sqrt{{(- 3)}^{2}} = 3$

查看试题解析
7. 下列命题中，是真命题的是（　　）

A、内错角相等 B、64的立方根是8 C、三角形的内角和等于180° D、相等的两个角是对顶角

查看试题解析
8. 下列各点中，在函数y＝﹣3x的图象上的是（　　）

A、 $(\frac{1}{3} ， 1)$ B、 $(- \frac{1}{3} ， 1)$ C、 $(- \frac{1}{3} ， - 1)$ D、（0，1）

查看试题解析
9. 如图，面积为3的正方形ABCD的顶点A在数轴上，且表示的数为﹣1，若AD＝AE ，则数轴上点E所表示的数为（　　）

A、 $\sqrt{3}$ ﹣1 B、 $\sqrt{3}$ +1 C、﹣ $\sqrt{3}$ +1 D、 $\sqrt{3}$

查看试题解析
10. 要使二次根式 $\sqrt{x - 3}$ 有意义，x的值不可以取（　　）

A、2 B、3 C、4 D、5

查看试题解析
11. 2023年杭州亚运会期间，吉祥物琼琼、宸宸、莲莲因其灵动可爱的形象受到了大家的喜爱．为了提高销量，某店家推出了吉祥物套装礼盒，一个套装礼盒里包含1个吉祥物宸宸玩偶和2个其他吉祥物的钥匙扣．已知一个玩偶的进价为60元，一个钥匙扣的进价为20元，该店家计划用5000元购进一批玩偶和钥匙扣，使得刚好配套，设购进x个玩偶，y个钥匙扣，则下列方程组正确的是（　　）

A、 ${\begin{array}{l} x = 2 y \\ 60 x + 20 y = 5000 \end{array}$ B、 ${\begin{array}{l} x = 2 y \\ 20 x + 60 y = 5000 \end{array}$ C、 ${\begin{array}{l} 2 x = y \\ 60 x + 20 y = 5000 \end{array}$ D、 ${\begin{array}{l} 2 x = y \\ 20 x + 60 y = 5000 \end{array}$

查看试题解析
12. 若直线y＝kx+b经过第一、二、四象限，则函数y＝bx﹣k的大致图象是（　　）

A、 B、 C、 D、

查看试题解析

二、填空题（本大题共4个小题，每小题2分，满分8分）

13. $\sqrt{81}$ 的算术平方根是

查看试题解析
14. 如图，AB∥CD ， ∠A＝37°，∠C＝63°，那么∠F的度数为．

查看试题解析
15. 如图，直线l₁：y＝x+1与直线l₂：y＝kx+b相交于点P（1，m），则关于x ， y的方程组 ${\begin{array}{l} y = x + 1 \\ y = k x + b \end{array}$ 的解为．

查看试题解析
16. 如图， $R t △ A B C$ 中， $A B = 9 ， B C = 6 ， ∠ B = 90 °$ ，将 $△ A B C$ 折叠，使 $A$ 点与 $B C$ 的中点 $D$ 重合，折痕为 $M N ，$ 则线段 $B N$ 的长为.

查看试题解析

三、解答题（本大题共8个小题，满分56分）

17.

(1)、计算： $(\sqrt{2} - π)^{0} + \sqrt{27} + | \sqrt{3} - 1 |$ ；

(2)、解方程组： ${\begin{array}{l} x + 2 y = 3 \\ 2 x - 4 y = - 10 \end{array}$ ．

查看试题解析
18. 如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，4），B（﹣3，2），C（2，0）．

(1)、在平面直角坐标系中，画出△ABC；

(2)、求△ABC的面积；

(3)、在图中作出△ABC关于x轴对称的△A^'B^'C^' ．

查看试题解析
19. 大泽山向外地运送一批葡萄，公路运输每千克需运费0.25元，运完这批葡萄还需其他费用800元；铁路运输每千克需运费0.6元．

(1)、若运输的这批葡萄为x千克，选择公路运输，所需费用为y₁元；选择铁路运输，所需费用为y₂元．请分别写出y₁ ， y₂与x之间的关系式．

(2)、若支出运费1500元，则选用哪种运输方式运输的葡萄多？

查看试题解析
20. 如图，已知∠1=∠2，∠C=∠D，求证：∠A=∠F．

查看试题解析
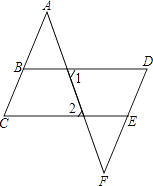21. 为积极落实“双减”政策，让作业布置更加精准高效，某校对八年级部分学生每天完成作业所用的时间进行调查，并用得到的数据绘制了如下不完整的统计图，如图，根据图中信息完成下列问题：

(1)、本次共调查了 ▲ 名学生，并补全上面条形统计图；

(2)、在扇形统计图中，每天完成作业所用时间为1.5小时的部分所对的圆心角度数是；

(3)、本次抽查学生每天完成作业所用时间的中位数为；众数为；

(4)、该校八年级有800名学生，请你估计八年级学生中，每天完成作业所用时间为0.5小时的学生有多少人？

查看试题解析
22. “劳动基地”是培养学生劳动意识和创新精神的重要平台，某校在校园一角开辟了一块四边形的“劳动基地”，如图，经过测量得知：∠B＝90°，AB＝6m ， BC＝8m ， CD＝24m ， AD＝26m ．

(1)、连接AC ，判断△ACD的形状并说明理由；

(2)、若在该基地上种植蔬菜，每平方米需要费用3元，试问种满这块基地共需费用多少元？

查看试题解析
23. 为迎接“创文创卫活动”，某市环卫局准备购买A、B两种型号的垃圾箱，买2个A型垃圾箱和1个B型垃圾箱共需100元；买1个A型垃圾箱和3个B型垃圾箱共需150元．

(1)、每个A型垃圾箱和B型垃圾箱各多少元？

(2)、购买A、B两种型号的垃圾箱共50个，其中A型垃圾箱a（0≤a≤16）个，求购买垃圾箱的总费用w（元）与A型垃圾箱a（个）之间的函数关系式，并说明总费用最少需要多少元？

查看试题解析
24. 如图，在平面直角坐标系中，直线y＝2x+4与x轴，y轴分别交于点A ， B两点；过点D（0，2）作直线CD与x轴交于点C ，交直线AB于点E ，且点E的横坐标为 $- \frac{4}{5}$ ．

(1)、直接写出点A ，点B的坐标；

(2)、求△ACE的面积；

(3)、如图乙，若点M是线段AB上一动点，连接OM ，过点O作ON⊥OM交直线CD于点N ，判断线段OM与ON的数量关系，并说明理由．

查看试题解析

	甲	乙	丙	丁
平均数	95	96	96	95
方差	2.5	2.4	2.3	2.5