吉林省长春市南关区重点学校2023-2024学年八年级上学期期末数学试卷

试卷更新日期：2024-04-16 类型：期末考试

进入出卷网下载

一、选择题（每小题3分，共24分）

1. 下列实数中是无理数的是（）

A、 $\sqrt{2}$ B、 $\sqrt{4}$ C、 $\frac{1}{3}$ D、3.14

查看试题解析
2. 若 $\sqrt{a} = 4$ ，则a的值为（　　）

A、2 B、16 C、﹣16 D、±16

查看试题解析
3. 在日本核电站排放核废水期间，我国某监测点监测到极微量的人工放射性核素碘﹣131，其浓度为0.0000963贝克/立方米．数据“0.0000963”用科学记数法可表示为（　　）

A、96.3×10⁶ B、963×10^﹣7 C、9.63×10^﹣5 D、0.963×10^﹣4

查看试题解析
4. 下列不能表示 $y$ 是 $x$ 的函数的是（）

A、
x 0 5 10 15
y 3 3.5 4 4.5
B、 C、 D、 $y = 2 x + 1$

查看试题解析
5. 在下列以线段a、b、c的长为三边的三角形中，不能构成直角三角形的是（　　）

A、a＝9，b＝41，c＝40 B、a＝b＝5， $c = 5 \sqrt{2}$ C、a：b：c＝3：4：5 D、a＝3，b＝12，c＝15

查看试题解析
6. 如图，在数轴上点A ， B所表示得数分别是﹣1，1，CB⊥AB ， BC＝1，以点A为圆心，AC长为半径画弧，交数轴于点D（点D在点B的右侧），则点D所表示的数是（　　）

A、 $\sqrt{5}$ B、 $\sqrt{5} - 1$ C、 $\sqrt{2}$ D、2﹣ $\sqrt{5}$

查看试题解析
7. 已知一次函数y＝kx﹣k ，当k＜0时，此函数的图象可以是（　　）

A、 B、 C、 D、

查看试题解析
8. 如图所示，点 $A (- \sqrt{2} ， 0)$ ，点 $B (0 ， - \sqrt{2})$ 分别在坐标轴上，第一象限中的点P坐标为（2，a），且满足S_△_ABP＝3S_△_ABO ，则a的值为（　　）

A、2 B、 $2 \sqrt{2} + 2$ C、 $2 \sqrt{2} - 2$ D、 $2 - 2 \sqrt{2}$

查看试题解析

二、填空题（每小题3分，共18分）

9. 分解因式：﹣am²+4am﹣4a＝．

查看试题解析
10. 函数 $y = \frac{\sqrt{x + 1}}{x + 1}$ 自变量x的取值范围是．

查看试题解析
11. 比 $\sqrt{3}$ 大且比 $\sqrt{7}$ 小的整数是．

查看试题解析
12. 平面直角坐标系中，点P（m﹣1，m+2）在第二象限，且点P到y轴的距离是1，则P的坐标为．

查看试题解析
13. 已知a^m＝3，aⁿ＝2，则a^m^＋n的值为.

查看试题解析
14. 如图，若正比例函数y＝kx图象与四条直线x＝﹣1，x＝2，y＝2，y＝4相交围成的长方形ABCD有公共点，则k的取值范围是．

查看试题解析

三、解答题（共78分）

15. 计算：

(1)、 $\sqrt{32} - 3 \sqrt{\frac{1}{2}} + \sqrt{2}$ ；

(2)、 $- 2^{2} + {(π - 2023)}^{0} - {(- \frac{1}{2})}^{- 1}$ ；

(3)、（m﹣2n）（m+2n）；

(4)、（6x⁴﹣8x³+2x²）÷（﹣2x²）．

查看试题解析
16. 解分式方程：

(1)、 $\frac{2}{x - 3} = 3$ ；

(2)、 $\frac{x - 2}{x + 2} - \frac{16}{x^{2} - 4} = 1$ ．

查看试题解析
17. 先化简，再求值： $(1 + \frac{2}{a + 1}) \div \frac{a^{2} + 6 a + 9}{a + 1}$ ，从﹣3，﹣1，2中选择合适的a的值代入求值．

查看试题解析
18. “低碳生活，绿色出行”是我们倡导的一种生活方式，有关部门随机调查了某单位员工上下班的交通方式，绘制了如下统计图，根据统计图，完成下列问题：

(1)、调查的总人数为．

(2)、补全条形统计图，交通方式为“骑自行车”所对的圆心角的度数为．

(3)、该单位共有300人，为了积极践行“低碳生活，绿色出行”这种生活方式，调查后开私家车的人上下班全部改为骑自行车，则现在骑自行车的人数约为多少人？

查看试题解析
19. 新冠疫情结束后，同学们迎来了期盼已久的校秋季运动会．某班检阅队伍需租用一批服装，经了解，在甲商店租用服装比在乙商店租用服装每套多10元，用600元在甲商店租用服装的数量与用500元在乙商店租用服装的数量相等．

(1)、求在甲、乙两个商店租用的服装每套各多少元？

(2)、若租用10套以上服装，甲商店给以每套九折优惠，该班准备租用20套服装，请问在哪家商店租用服装的费用较少？并说明理由．

查看试题解析
20. 图①、图②、图③均是6×6的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点叫做格点，如图中的各点均在格点上．只用无刻度的直尺，分别在给定的网格中按要求画图，保留作图痕迹．

(1)、在图①中作出△ABC的角平分线BM ．

(2)、在图②中作出△DEF的角平分线EN ．

(3)、在图③中作出△GHI的角平分线HP ．

查看试题解析
21. 已知：如图，在四边形ABCD中，∠BAC＝∠ACD＝90°，AB＝ $\frac{1}{2}$ CD，点E是CD的中点.

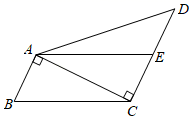(1)、求证：AE＝BC；

(2)、若AC＝4，AD＝4 $\sqrt{2}$ ，求四边形ABCE的面积.

查看试题解析
22. 在平面直角坐标系中，点A（a ， 1），B（4，b）在直线 $y = \frac{3}{5} x + \frac{8}{5}$ 上，分别过点A、B作x轴，y轴的平行线交于点C ．

(1)、a＝， b＝；

(2)、求过点C且平行于AB的直线MN的解析式．

查看试题解析
23.
方法原型：如图①点B、A、C在同一条直线上，DB⊥BC ， EC⊥BC且∠DAE＝90°，AD＝AE ，则△DBA≌△ACE ．

(1)、问题解决：在上述条件下，BC、BD、CE之间的数量关系为．

(2)、拓展延伸：如图②，Rt△ABC中，∠ACB＝90°， $C B = A C = 2 \sqrt{2}$ ，点D为射线AB上一点，以CD为直角边在CD的右侧作等腰Rt△CDE ，使∠CDE＝90°．
i ．如图②，连结AE ，当AD＝3时，求△ADE的面积．
ii ．如图③，当AD＝5时，请直接写出点E到边BC的距离．

查看试题解析
24. 如图所示，已知△ABC中，∠C＝90°，AB＝5，BC＝3，动点P从点C出发沿C﹣A﹣B以每秒2个单位的速度运动，到达点B时停止运动，设运动时间为t秒（t＞0）．

(1)、AC＝．

(2)、 $t = \frac{1}{2}$ 时，AP的长为．点P在AB边上时，线段AP的长为（用含t的代数式表示）．

(3)、当点P在AB的中垂线上时，求t的值．

(4)、如图②，当点P在AB上运动时，连结CP ，作点A关于CP的对称点A^' ，连结A^'C ， A^'P ．当存在△A^'PC的边与△ABC的边平行时，直接写出t的值．

查看试题解析

x	0	5	10	15
y	3	3.5	4	4.5