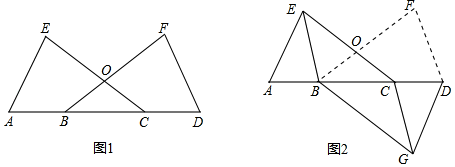2024年初中数学人教版八年级下学期期中模拟考试卷 05
试卷更新日期:2024-04-16 类型:期中考试
一、单选题
-
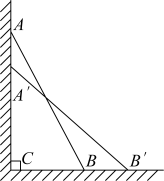
1. 下列计算正确的是( )A、 B、 C、 D、2. 下列长度的三条线段,能组成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,3. 在Rt△ABC中,CD是斜边AB上的中线,则以下判断正确的是( )A、CD=2AB B、CD=AC C、CD=BC D、CD=AD=BD4. 老师布置了任务:过直线上一点C作的垂线.在没有直角尺的情况下,嘉嘉和淇淇利用手头的学习工具给出了如图所示的两种方案,下列判断正确的是( )
方案Ⅰ:
①利用一把有刻度的直尺在上量出 . ②分别以D,C为圆心,以和为半径画圆弧,两弧相交于点E.③作直线 , 即为所求的垂线.
方案Ⅱ:
取一根笔直的木棒,在木棒上标出M,N两点.①使点M与点C重合,点N对应的位置标记为点Q.②保持点N不动,将木棒绕点N旋转,使点M落在上,将旋转后点M对应的位置标记为点R.③将延长,在延长线上截取线段 , 得到点S.④作直线 , 即为所求直线.
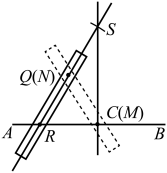 A、Ⅰ可行、Ⅱ不可行 B、Ⅰ不可行、Ⅱ可行 C、Ⅰ、Ⅱ都可行 D、Ⅰ、Ⅱ都不可行5. 如图,在平面直角坐标系中,正方形的两个顶点A、B是坐标轴上的动点,若正方形的边长为4,则线段长的最大值是( )
A、Ⅰ可行、Ⅱ不可行 B、Ⅰ不可行、Ⅱ可行 C、Ⅰ、Ⅱ都可行 D、Ⅰ、Ⅱ都不可行5. 如图,在平面直角坐标系中,正方形的两个顶点A、B是坐标轴上的动点,若正方形的边长为4,则线段长的最大值是( )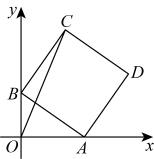 A、 B、 C、 D、86. 如图,与均为直角三角形,且 , , , 点E是的中点,则的长为( )
A、 B、 C、 D、86. 如图,与均为直角三角形,且 , , , 点E是的中点,则的长为( )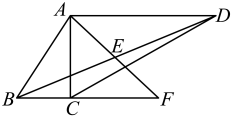 A、 B、 C、2 D、37. 我国是最早了解勾股定理的国家之一,下面四幅图中,不能证明勾股定理的是( )A、
A、 B、 C、2 D、37. 我国是最早了解勾股定理的国家之一,下面四幅图中,不能证明勾股定理的是( )A、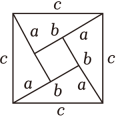 B、
B、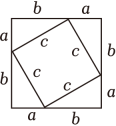 C、
C、 D、
D、 8. 定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.已知在“等对角四边形”中, , , 则边的长是( )A、 B、 C、或 D、或
8. 定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.已知在“等对角四边形”中, , , 则边的长是( )A、 B、 C、或 D、或二、填空题
-
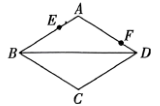
9. =10. 如图,在周长为16的菱形中,点E、F分别在边上, , P为上一动点,则线段长度的最小值为.
 11. 已知|2009﹣a|+=a , 则a﹣20092= .12. 一个长方形的长减少2cm,宽增加1cm,就成为一个正方形,并且正方形的面积比原长方形的面积小 , 则原长方形的面积为。13. 如图,在平面直角坐标系中,点的坐标为 , 点的坐标为 , 点在轴的正半轴上,且 , 在平面直角坐标系内确定点 , 使得以点为顶点的四边形是平行四边形,则点的坐标为 .
11. 已知|2009﹣a|+=a , 则a﹣20092= .12. 一个长方形的长减少2cm,宽增加1cm,就成为一个正方形,并且正方形的面积比原长方形的面积小 , 则原长方形的面积为。13. 如图,在平面直角坐标系中,点的坐标为 , 点的坐标为 , 点在轴的正半轴上,且 , 在平面直角坐标系内确定点 , 使得以点为顶点的四边形是平行四边形,则点的坐标为 .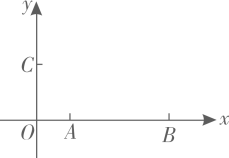 14. 在高5m,长13m的一段台阶上铺上地毯,台阶的剖面如图所示,地毯的长度至少需要 m.
14. 在高5m,长13m的一段台阶上铺上地毯,台阶的剖面如图所示,地毯的长度至少需要 m.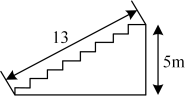 15. 如图,在正方形ABCD中,AB=4,AC与BD相交于点O,M是AO的中点,P,Q为对角线BD上的两点,若PQ= , 则PM+CQ的最小值为 .
15. 如图,在正方形ABCD中,AB=4,AC与BD相交于点O,M是AO的中点,P,Q为对角线BD上的两点,若PQ= , 则PM+CQ的最小值为 .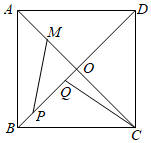
三、解答题
-
16. △ABC的三边长分别为5,x-2,x+1,若该三角形是以x+1为斜边的直角三角形,求x的值.17. 如图,在矩形中,点E、F分别在和上,若 . 求证:四边形是平行四边形;
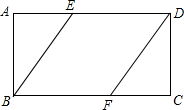 18. 已知△ACD中,AC=AD,∠CAD=α,∠PAC=30°,将点C关于直线AP对称,得到点B,连接BA.
18. 已知△ACD中,AC=AD,∠CAD=α,∠PAC=30°,将点C关于直线AP对称,得到点B,连接BA. (1)、连接BD,
(1)、连接BD,①依题意,在图1中补全图形;
②若α=80°,则∠BDC的度数为 ▲ ;
③当α的度数发生变化时,请探究∠BDC的大小是否改变.若不变,求出∠BDC的度数 ;若改变,请说明理由.
(2)、如图2,以AB为斜边作直角三角形ABE,使得∠B=∠ACD, 连接CE,DE.若α=90°.求证:CE⊥ED.四、实践探究题
-
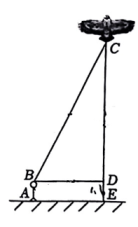
19. 某校八年级的王明和孙亮两位同学在学习了“勾股定理”之后,为了测得风筝的垂直高度CE,他们进行了如下操作:
①测得BD的长度为8米;(注:BD⊥CE)
②根据手中剩余线的长度计算出风筝线BC的长为17米:
③牵线放风筝的王明身高AB=1.6米:(注:AB=DE)
求风筝的垂直高度CE;
 20.(1)、【阅读理解】如图1, , 的面积与的面积相等吗?为什么?
20.(1)、【阅读理解】如图1, , 的面积与的面积相等吗?为什么?
 (2)、【类比探究】问题①,如图2,在正方形的右侧作等腰 , , , 连接 , 求的面积.
(2)、【类比探究】问题①,如图2,在正方形的右侧作等腰 , , , 连接 , 求的面积.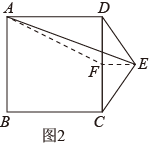 (3)、【拓展应用】问题②,如图3,在正方形的右侧作正方形 , 点B,C,E在同一直线上, , 连接 , , , 直接写出的面积.
(3)、【拓展应用】问题②,如图3,在正方形的右侧作正方形 , 点B,C,E在同一直线上, , 连接 , , , 直接写出的面积.
 21. 综合与实践
21. 综合与实践【问题发现】如图1,把两个面积都为1cm2的小正方形分别沿对角线剪开,将所得的4个直角三角形拼成一个大正方形,则该大正方形的边长为 ▲ cm.
【知识迁移】若一个圆与一个正方形的面积都是2πcm2 , 设这个圆的周长为C这个正方形的周长为C圆 , 则C圆 ▲ C正(填“=”或“<”或“>”).
【拓展延伸】李明想用一块面积为400cm2的正方形纸片(如图2所示),沿着边的方向截出一块面积为300cm2的长方形纸片,使它的长宽之比为5:4.李叨能用这块纸片裁出符合要求的纸片吗?请说明理由.
五、综合题
-
22. 如图是的正方形网格,每个小正方形的边长为1,小正方形的顶点称为格点. , , 均为格点.在给定的网格中.
 (1)、线段的长等于;(2)、在给定的网格中画一个 , 使与关于某条直线对称,且 , , 为格点(画出一个满足题意的三角形并保留作图痕迹即可).
(1)、线段的长等于;(2)、在给定的网格中画一个 , 使与关于某条直线对称,且 , , 为格点(画出一个满足题意的三角形并保留作图痕迹即可).