2024年初中数学人教版八年级下学期期中模拟考试卷 04
试卷更新日期:2024-04-16 类型:期中考试
一、单选题
-
1. 计算的结果为( )A、-11 B、11 C、±11 D、1212. 下列各式计算正确的是( )A、 B、 C、 D、3. 如图,平行四边形四个内角平分线相交,构成四边形 , 则四边形的形状是( )
 A、任意四边形 B、正方形 C、矩形 D、菱形4. 如图,在中, , , , 点是的中点,连接 , 则的长为( )
A、任意四边形 B、正方形 C、矩形 D、菱形4. 如图,在中, , , , 点是的中点,连接 , 则的长为( ) A、 B、 C、3 D、45. 如图,在中, , , 分别是 , , 的中点.若 , , 则四边形的周长是( )
A、 B、 C、3 D、45. 如图,在中, , , 分别是 , , 的中点.若 , , 则四边形的周长是( ) A、 B、 C、 D、6. 如图,四边形ABCD的对角线互相平分,要使它成为矩形,那么需要添加的条件是( )
A、 B、 C、 D、6. 如图,四边形ABCD的对角线互相平分,要使它成为矩形,那么需要添加的条件是( ) A、AB=BC B、AC垂直BD C、∠A=∠C D、AC=BD7. 如图 , 平行四边形中, , 为锐角.要在对角线上找点N, , 使四边形为平行四边形,现有图中的甲、乙、丙三种方案,则正确的方案是( )
A、AB=BC B、AC垂直BD C、∠A=∠C D、AC=BD7. 如图 , 平行四边形中, , 为锐角.要在对角线上找点N, , 使四边形为平行四边形,现有图中的甲、乙、丙三种方案,则正确的方案是( )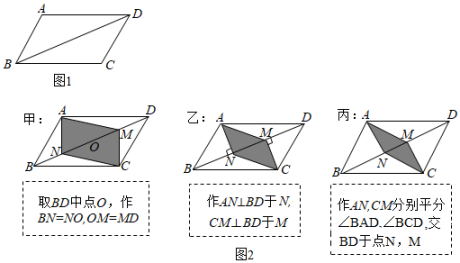 A、只有甲、乙才是 B、只有甲、丙才是 C、只有乙、丙才是 D、甲、乙、丙都是8. 如图,正方形ABCO和正方形DEFO的顶点A , E , O在同一直线l上,且EF= , AB=3,给出下列结论:①∠COD=45°;②AE=5;③CF=BD=;④S△COF=3,其中正确的个数为 ( )
A、只有甲、乙才是 B、只有甲、丙才是 C、只有乙、丙才是 D、甲、乙、丙都是8. 如图,正方形ABCO和正方形DEFO的顶点A , E , O在同一直线l上,且EF= , AB=3,给出下列结论:①∠COD=45°;②AE=5;③CF=BD=;④S△COF=3,其中正确的个数为 ( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
9. 若 , 则a的值是 .10. 如图,在平行四边形中,已知 , , 的角平分线交边于点E,则的长为.
 11. 如图,用长为a米的铝合金制成如图窗框,已知矩形AGHD,矩形BFEG,矩形EFCH的面积均相等,设AD的长为b米,则AB的长是米.(用含a,b的代数式表示)
11. 如图,用长为a米的铝合金制成如图窗框,已知矩形AGHD,矩形BFEG,矩形EFCH的面积均相等,设AD的长为b米,则AB的长是米.(用含a,b的代数式表示)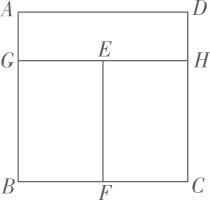 12. 如图,把一张长方形纸片ABCD沿EF折叠后,点C , D分别落在的位置上,交AD于点G . 已知 , 那么度.
12. 如图,把一张长方形纸片ABCD沿EF折叠后,点C , D分别落在的位置上,交AD于点G . 已知 , 那么度. 13. 某会展中心在会展期间准备将高5m、长13m、宽2m的楼道铺上地毯,已知地毯每平方米20元,请你帮助计算一下,铺完这个楼道至少需要元.
13. 某会展中心在会展期间准备将高5m、长13m、宽2m的楼道铺上地毯,已知地毯每平方米20元,请你帮助计算一下,铺完这个楼道至少需要元. 14. 如图,在矩形中, , 点在边上,且 , 、分别是边、上的动点,且 , 是线段上的动点,连接 , 若则线段的长为 .
14. 如图,在矩形中, , 点在边上,且 , 、分别是边、上的动点,且 , 是线段上的动点,连接 , 若则线段的长为 . 15. 如图1,有一张矩形纸片 , 已知 , , 现将纸片进行如下操作:现将纸片沿折痕进行折叠,使点落在边上的点处,点在上(如图2),则;然后将绕点旋转到 , 当过点时旋转停止,则的长度为 .
15. 如图1,有一张矩形纸片 , 已知 , , 现将纸片进行如下操作:现将纸片沿折痕进行折叠,使点落在边上的点处,点在上(如图2),则;然后将绕点旋转到 , 当过点时旋转停止,则的长度为 .
三、解答题
-
16. 如图,在中,点E,F在对角线上,且 , 连接 , , 求证:.
 17. 已知:如图,、分别是▱的边、上的点,且 .
17. 已知:如图,、分别是▱的边、上的点,且 .
求证: . 18. 如图,在△CBD中,CD=BD , CD⊥BD,BE平分∠CBA交CD于点F , CE⊥BE垂足是E,CE与BD交于点A,求证,
18. 如图,在△CBD中,CD=BD , CD⊥BD,BE平分∠CBA交CD于点F , CE⊥BE垂足是E,CE与BD交于点A,求证, (1)、BF=AC;(2)、BE是AC的中垂线;(3)、若AD=2,求BD的长.
(1)、BF=AC;(2)、BE是AC的中垂线;(3)、若AD=2,求BD的长.四、实践探究题
-
19. 阅读材料,解答下面问题:我们新定义一种三角形,两边的平方和等于第三边平方2倍的三角形叫做奇异三角形.(1)、理解并填空:
①根据奇异三角形的定义,请你判断:等边三角形一定(填“是”或“不是”)奇异三角形;
②若某三角形的三边长分别为1, , 2,则该三角形(填“是”或“不是”)奇异三角形;
(2)、探究:在中,两边长分别是a,c,且 , , 则这个三角形是否是奇异三角形?请说明理由.20. 综合与实践问题情境:某消防队在一次应急演练中,消防员架起一架长25m的云梯AB , 如图,云梯斜靠在一面墙上,这时云梯底端距墙脚的距离BC=7m , ∠DCE=90°.
 (1)、独立思考:
(1)、独立思考:这架云梯顶端距地面的距离AC有多高?
(2)、深入探究:消防员接到命令,按要求将云梯从顶端A下滑到A′位置上(云梯长度不改变),AA′=4m , 那么它的底部B在水平方向滑动到B′的距离BB′也是4m吗?若是,请说明理由;若不是,请求出BB′的长度.
(3)、问题解决:在演练中,高24.3m的墙头有求救声,消防员需调整云梯去救援被困人员.经验表明,云梯靠墙摆放时,如果云梯底端离墙的距离不小于云梯长度的 , 则云梯和消防员相对安全.在相对安全的前提下,云梯的顶端能否到达24.3m高的墙头去救援被困人员?
五、综合题
-
21. 如图,在▱中,点、分别在、上,与相交于点 , 且.
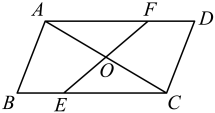 (1)、求证:≌;(2)、连接 , , 求证:四边形是平行四边形.22. 已知:如图,在中, , 点D是边的中点, , 联结 .
(1)、求证:≌;(2)、连接 , , 求证:四边形是平行四边形.22. 已知:如图,在中, , 点D是边的中点, , 联结 . (1)、求证:;(2)、如果平分 , 求证: .23.
(1)、求证:;(2)、如果平分 , 求证: .23. (1)、组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在中, , D、A、E三点都在直线l上,并且有 , 其中α为任意锐角或钝角.请问结论是否成立?如成立,请你给出证明;若不成立,请说明理由.(2)、数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过的边向外作正方形和正方形 , 是边上的高,延长交于点I,求证:I是的中点.(3)、某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:在中, , , 直线l经过点A,直线l,直线l,垂足分别为点D、E.证明: .
(1)、组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在中, , D、A、E三点都在直线l上,并且有 , 其中α为任意锐角或钝角.请问结论是否成立?如成立,请你给出证明;若不成立,请说明理由.(2)、数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过的边向外作正方形和正方形 , 是边上的高,延长交于点I,求证:I是的中点.(3)、某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:在中, , , 直线l经过点A,直线l,直线l,垂足分别为点D、E.证明: .