四川省德阳市中江县2023-2024学年七年级下学期数学月考考试试卷(3月)
试卷更新日期:2024-04-16 类型:月考试卷
一、选择题(本大题共12个小题,每小题4分,满分48分)
-
1. 在图示的四个汽车标志图案中,能用平移变换来分析其形成过程的图案是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,两条直线 , 交于点 , 射线是的平分线,若 , 则等于( )
2. 如图,两条直线 , 交于点 , 射线是的平分线,若 , 则等于( ) A、140° B、120° C、100° D、80°3. 下列说法中正确的有( )A、 B、是5的一个平方根 C、 D、4. 点为直线外一点,点、、为直线上三点, , , , 则点到直线的距离为( )A、等于 B、等于 C、等于 D、不大于5. 如图,下列说法错误的是( )
A、140° B、120° C、100° D、80°3. 下列说法中正确的有( )A、 B、是5的一个平方根 C、 D、4. 点为直线外一点,点、、为直线上三点, , , , 则点到直线的距离为( )A、等于 B、等于 C、等于 D、不大于5. 如图,下列说法错误的是( ) A、与是对顶角 B、与是内错角 C、与是同位角 D、与是同旁内角6. 一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,则∠DBC的度数为( )
A、与是对顶角 B、与是内错角 C、与是同位角 D、与是同旁内角6. 一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,则∠DBC的度数为( )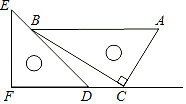 A、10° B、15° C、18° D、30°7. 下列四个命题中,真命题有( )A、直线外一点到这条直线的垂线段,叫做点到直线的距离 B、过一点有且只有一条直线与已知直线垂直 C、两条直线被第三条直线所截,内错角相等 D、平行于同一条直线的两条直线平行8. 如图,河道l的一侧有A、B两个村庄,现要铺设一条引水管道把河水引向A、B两村,下列四种方案中最节省材料的是( )
A、10° B、15° C、18° D、30°7. 下列四个命题中,真命题有( )A、直线外一点到这条直线的垂线段,叫做点到直线的距离 B、过一点有且只有一条直线与已知直线垂直 C、两条直线被第三条直线所截,内错角相等 D、平行于同一条直线的两条直线平行8. 如图,河道l的一侧有A、B两个村庄,现要铺设一条引水管道把河水引向A、B两村,下列四种方案中最节省材料的是( ) A、
A、 B、
B、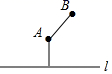 C、
C、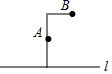 D、
D、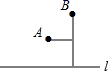 9. 如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心的光线相交于点 , 点为焦点.若 , , 则的度数为( )
9. 如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心的光线相交于点 , 点为焦点.若 , , 则的度数为( ) A、25° B、20° C、30° D、35°10. 利用计算器计算出的下表中各数的算术平方根如下:
A、25° B、20° C、30° D、35°10. 利用计算器计算出的下表中各数的算术平方根如下:…
…
…
0.25
0.7906
2.5
7.906
25
79.06
250
…
根据以上规律,若 , , 则( )
A、37.9 B、379 C、12 D、12011. 如图, , 且 , 那么图中与相等的角(不包括)的个数是( ) A、2 B、4 C、5 D、612. 如图, , F为上一点, , 且平分 , 过点F作于点G,且 , 则下列结论:①;②;③平分;④平分 . 其中正确结论的个数是( )
A、2 B、4 C、5 D、612. 如图, , F为上一点, , 且平分 , 过点F作于点G,且 , 则下列结论:①;②;③平分;④平分 . 其中正确结论的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(本大题共7个小题,每小题4分,本大题满分28分)
-
13. 3的平方根是14. 把命题“同角的余角相等”写成“如果…,那么….”的形式为:.15. 和互为相反数,则的值为.16. 已知:对于实数、 , 定义一种运算“”为: , 则方程的解为.17. 图1是一张足够长的纸条,其中 , 点、分别在、上,如图2,将纸条折叠,使与重合,得折痕 , 若记 , 则.

图1 图2
18. 已知 , 以为顶点作射线 , .若 , , 则的度数为.19. 已知( , 且为整数)条直线中只有两条直线平行,且任何三条直线都不交于同一个点.如图,当时,共有2个交点;当时,共有5个交点;当时,共有9个交点;…依此规律,当条直线相交时,共有交点个数为为.
三、解答题(6个小题,共74分)
-
20. 计算:(1)、;(2)、;(3)、.21. 如图,直线、、相交于点 , , 平分.
 (1)、请直接写出图中所有与互余的角:;(2)、若 , 求与的度数.22. 已知是9的算术平方根,是的立方根,求的平方根.23. 如图,在三角形中,于 , 点是上一点,于交于点 , 点是延长线上一点,连接 , .
(1)、请直接写出图中所有与互余的角:;(2)、若 , 求与的度数.22. 已知是9的算术平方根,是的立方根,求的平方根.23. 如图,在三角形中,于 , 点是上一点,于交于点 , 点是延长线上一点,连接 , . (1)、求证:;(补全证明过程,并在括号内填写推理的依据)
(1)、求证:;(补全证明过程,并在括号内填写推理的依据)证明: , (已知),
(① )
② ▲ (同位角相等,两直线平行),
(③ )
(已知),
④ ▲ )(⑤ )
(⑥ ).
(2)、若 , , 求的度数.24. 画图并填空:如图,三角形的顶点都在方格纸的格点上,每个格子的边长为1个单位长度,将三角形向上平移3个单位长度,向左平移2个单位长度得到三角形. (1)、画出表示点到的距离的线段;(2)、在图中画出平移后的三角形;(3)、若连接 , , 则这两条线段的关系是;(4)、在图中能使的面积等于三角形面积的格点的个数有个(点异于).25.(1)、【探索发现】已知:如图1, , 点在 , 之间,连接 , .求证:.
(1)、画出表示点到的距离的线段;(2)、在图中画出平移后的三角形;(3)、若连接 , , 则这两条线段的关系是;(4)、在图中能使的面积等于三角形面积的格点的个数有个(点异于).25.(1)、【探索发现】已知:如图1, , 点在 , 之间,连接 , .求证:.下面是小刚同学添加辅助线的方法:如图2,过点作.

图1 图2

图3 图4
请你写出小刚同学完整的证明方法;
(2)、【深入思考】如图3,点 , 分别是射线 , 上一点,点是线段上一点,连接并延长,交直线于点 , 连接 , , 若 , 求证:;(3)、【拓展应用】如图4,在(2)的条件下, , 平分 , 平分 , 与交点 , 若 , , .求的度数.