四川省德阳市中江县2023-2024学年九年级下学期数学月考考试试卷(3月)
试卷更新日期:2024-04-16 类型:月考试卷
一、选择题(本大题共12小题,每小题4分,共48分.在每小所给出的四个选项中,只有一项是符合题目要求的,请将正确选项的序号填涂在答题卡上)
-
1. 的绝对值是( )A、2024 B、 C、 D、2. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列事件中,是必然事件的是( )A、乘坐公共汽车恰好有座位 B、小明期末考试会考满分 C、中江明天会下雪 D、三角形的内角和是4. 在平面直角坐标系中,点一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 不等式组的解集在数轴上表示正确的是( )A、
3. 下列事件中,是必然事件的是( )A、乘坐公共汽车恰好有座位 B、小明期末考试会考满分 C、中江明天会下雪 D、三角形的内角和是4. 在平面直角坐标系中,点一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 不等式组的解集在数轴上表示正确的是( )A、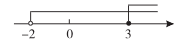 B、
B、 C、
C、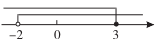 D、
D、 6. 下列运算正确的是( )A、 B、 C、 D、7. 关于一次函数 , 下列结论正确的是( )A、图象过点 B、其图象可由的图象向上平移3个单位长度得到 C、随的增大而增大 D、图象经过一、二、三象限8. 若关于x的一元二次方程有实数根,则k的值可以是( )A、2 B、 C、 D、39. 如图,点D , E分别在的边AB , AC上,且 , 若 , , 则( )
6. 下列运算正确的是( )A、 B、 C、 D、7. 关于一次函数 , 下列结论正确的是( )A、图象过点 B、其图象可由的图象向上平移3个单位长度得到 C、随的增大而增大 D、图象经过一、二、三象限8. 若关于x的一元二次方程有实数根,则k的值可以是( )A、2 B、 C、 D、39. 如图,点D , E分别在的边AB , AC上,且 , 若 , , 则( ) A、4.5 B、6 C、8 D、910. 如图,点P , Q在反比例函数的图象上,点M在x轴上,点N在y轴上,下列说法正确的是( )
A、4.5 B、6 C、8 D、910. 如图,点P , Q在反比例函数的图象上,点M在x轴上,点N在y轴上,下列说法正确的是( ) A、图1、图2中阴影部分的面积分别为2,4 B、图1、图2中阴影部分的面积分别为1,2 C、图1、图2中阴影部分的面积之和为8 D、图1、图2中阴影部分的面积之和为311. 如图,已知AB是的直径,弦 , 垂足为E , , , 则CD的长为( )
A、图1、图2中阴影部分的面积分别为2,4 B、图1、图2中阴影部分的面积分别为1,2 C、图1、图2中阴影部分的面积之和为8 D、图1、图2中阴影部分的面积之和为311. 如图,已知AB是的直径,弦 , 垂足为E , , , 则CD的长为( ) A、 B、 C、 D、12. 如图,正方形ABCD中,点E、F分别在边AD、AB上, , , DF与CE交于点M , AC与DF交于点N . 有如下结论:①;②;③;④ . 上述结论中,所有正确结论的个数有( )
A、 B、 C、 D、12. 如图,正方形ABCD中,点E、F分别在边AD、AB上, , , DF与CE交于点M , AC与DF交于点N . 有如下结论:①;②;③;④ . 上述结论中,所有正确结论的个数有( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题(本大题共6小题,每小题4分,共24分,不需写出解答过程,请把答案直接填写在答题卡相应位置上)
-
13. 据报道,2023年“十一”假期,某地A级旅游景区共接待游客151100人次,数字151100用科学记数法表示是 .14. 甲、乙、丙、丁四支女子花样游泳队的人数相同,且平均身高都是 , 身高的方差分别是 , , , , 则身高比较整齐的游泳队是 .15. 已知 , 是方程的两个根,则的值是 .16. 如图,过原点,且分别与两坐标轴交于点A , B , 点A的坐标为 , M是第三象限内上一点, , 则的半径为 .
 17. 已知 , 若关于x的分式方程有正整数解,则整数m的值是 .18. 如图,在中, , AD平分 , 点E在AD上,射线BE交AC于点F . 若 , , 则AF的长是 .
17. 已知 , 若关于x的分式方程有正整数解,则整数m的值是 .18. 如图,在中, , AD平分 , 点E在AD上,射线BE交AC于点F . 若 , , 则AF的长是 .
三、解答题(本大题共7小题,共78分.解答时将文字说明、证明过程或演算步骤写在答题卡相应的位置上)
-
19. 计算:20. 近几年,“碳中和、碳达峰”成为高频热词.为了解学生对“碳中和、碳达峰”知识的知晓情况,某校团委随机对该校九年级部分学生进行了问卷调查,调查结果共分成四个类别:A表示“从未听说过”,B表示“不太了解”,C表示“比较了解”,D表示“非常了解”,根据调查统计结果,绘制成两种不完整的统计图,请结合统计图,回答下列问题.
 (1)、参加这次调查的学生总人数为人;(2)、扇形统计图中,B部分扇形所对应的圆心角是;(3)、将条形统计图补充完整;(4)、在D类的学生中,有2名男生和2名女生,现需从这4名学生中随机抽取2名“碳中和、碳达峰”知识的义务宣讲员,请利用画树状图或列表的方法,求所抽取的2名学生恰好是1名男生和1名女生的概率.21. 已知一次函数与反比例函数的图象交于A , B两点,且点A的坐标为 .
(1)、参加这次调查的学生总人数为人;(2)、扇形统计图中,B部分扇形所对应的圆心角是;(3)、将条形统计图补充完整;(4)、在D类的学生中,有2名男生和2名女生,现需从这4名学生中随机抽取2名“碳中和、碳达峰”知识的义务宣讲员,请利用画树状图或列表的方法,求所抽取的2名学生恰好是1名男生和1名女生的概率.21. 已知一次函数与反比例函数的图象交于A , B两点,且点A的坐标为 . (1)、求m的值及反比例函数的解析式;(2)、连接OA , OB , 求的面积;(3)、观察图象,请直接写出的解集.22. 如图,在菱形ABCD中,P是它对角线上面的一个点,连接CP后并延长,交AD于点E , 交BA的延长线于点F .
(1)、求m的值及反比例函数的解析式;(2)、连接OA , OB , 求的面积;(3)、观察图象,请直接写出的解集.22. 如图,在菱形ABCD中,P是它对角线上面的一个点,连接CP后并延长,交AD于点E , 交BA的延长线于点F . (1)、求证:;(2)、如果 , , 求线段PC的长.23. 某商场购进了A , B两种商品,若销售10件A商品和20件B商品,则可获利280元;若销售20件A商品和30件B商品,则可获利480元.(1)、求A , B两种商品每件的利润;(2)、已知A商品的进价为24元/件,目前每星期可卖出200件A商品,市场调查反映:如调整A商品价格,每降价1元,每星期可多卖出20件,如何定价才能使A商品的利润最大?最大利润是多少?
(1)、求证:;(2)、如果 , , 求线段PC的长.23. 某商场购进了A , B两种商品,若销售10件A商品和20件B商品,则可获利280元;若销售20件A商品和30件B商品,则可获利480元.(1)、求A , B两种商品每件的利润;(2)、已知A商品的进价为24元/件,目前每星期可卖出200件A商品,市场调查反映:如调整A商品价格,每降价1元,每星期可多卖出20件,如何定价才能使A商品的利润最大?最大利润是多少?

