2024年人教版中考数学二轮复习专题18 图形的旋转、平移与轴对称

试卷更新日期：2024-04-16 类型：二轮复习

进入出卷网下载

一、单选题

1. 如图，将 $△ A B C$ 绕顶点A逆时针旋转70°，得到 $△ A D E$ ，若 $∠ C = 2 ∠ D = 104 °$ ，则 $∠ 1$ 的度数为（）

A、22° B、24° C、35° D、46°

查看试题解析
2. 如图，已知 $A B ∥ C D$ ，点E，F分别在直线 $A B ， C D$ 上，点P在 $A B ， C D$ 之间且在 $E F$ 的左侧.若将射线 $E A$ 沿 $E P$ 折叠，射线 $F C$ 沿 $F P$ 折叠，折叠后的两条射线互相垂直，则 $∠ E P F$ 的度数为（）

A、 $45 °$ B、 $135 °$ C、 $45 °$ 或 $135 °$ D、 $45 °$ 或 $90 °$ 或 $135 °$

查看试题解析
3. 如图，在四边形纸片ABCD中，AD∥BC ， AB＝10，∠B＝60°，将纸片折叠，使点B落在AD边上的点G处，折痕为EF ，若∠BFE＝45°，则BF的长为（）

A、5 B、 $3 \sqrt{5}$ C、 $5 \sqrt{3}$ D、 $\frac{\sqrt{3}}{5}$

查看试题解析
4. 如图矩形ABCD由矩形EBGF逆时针旋转一个锐角得到，点C在边EF上，过点E作AD平行线得矩形ANMD，则要知道矩形ANMD的面积只需知道（）

A、S_△_BEC B、S_△B_GC C、S_△E_CM D、S_△C_GF

查看试题解析
5. 如图，将 $Rt △ A B C$ 沿 $B C$ 方向平移得到 $Rt △ D E F$ ，若 $A B = 10 cm$ ， $B E = 6 cm$ ， $D H = 4 cm$ ，则图中阴影部分面积为（）

A、 $47 {cm}^{2}$ B、 $48 {cm}^{2}$ C、 $49 {cm}^{2}$ D、 $50 {cm}^{2}$

查看试题解析
6. 下列命题是真命题的是（）

A、平行四边形的对角线相等 B、经过旋转，对应线段平行且相等 C、两组对角分别相等的四边形是平行四边形 D、两边相等的两个直角三角形全等

查看试题解析
7. 如图，在菱形纸片 $A B C D$ 中， $∠ A B C = 60 °$ ， E是 $C D$ 边的中点，将菱形纸片沿过点A的直线折叠，使点B落在直线 $A E$ 上的点G处，折痕为 $A F$ ， $F G$ 与 $C D$ 交于点H，有如下结论：① $∠ C F H = 30 °$ ；② $D E = \frac{\sqrt{3}}{3} A E$ ；③ $C H = G H$ ；④ $S_{△ A B F} ： S_{四边形 A F C D} = 3 ： 5$ ，上述结论中，所有正确结论的序号是（）

A、①②④ B、①②③ C、①③④ D、①②③④

查看试题解析
8. 如图，四边形ABCD中，AB=AD，点 $B$ 关于 $A C$ 的对称点B′恰好落在CD上，若 $∠ B A D = α$ ，则 $∠ A C B$ 的度数为（）

A、 $45 °$ B、 $α - 45 °$ C、 $\frac{1}{2} α$ D、 $90 ° - \frac{1}{2} α$

查看试题解析
9. 如图，在△ABC中，∠BAC=90°，AB=AC=3，D，E分别在边AB，AC上，且DE∥BC，将△ABC沿DE翻折，点A的对应点为A'，A'D和A'E分别交BC于G，F，若A'F=1，则四边形DEFG的面积为（）

A、 $\frac{3}{2}$ B、2 C、 $\frac{5}{2}$ D、3

查看试题解析
10. 如图，已知长方形纸片 ABCD，点E，F分别在边AD和BC上，且∠EFC=53°，H和G 分别是边AD和 BC 上的动点，现将点 A，B 沿 EF 向下折叠至点N，M 处，将点 C，D沿GH 向上折叠至点P，K 处，若 MN∥PK，则∠KHD的度数为（）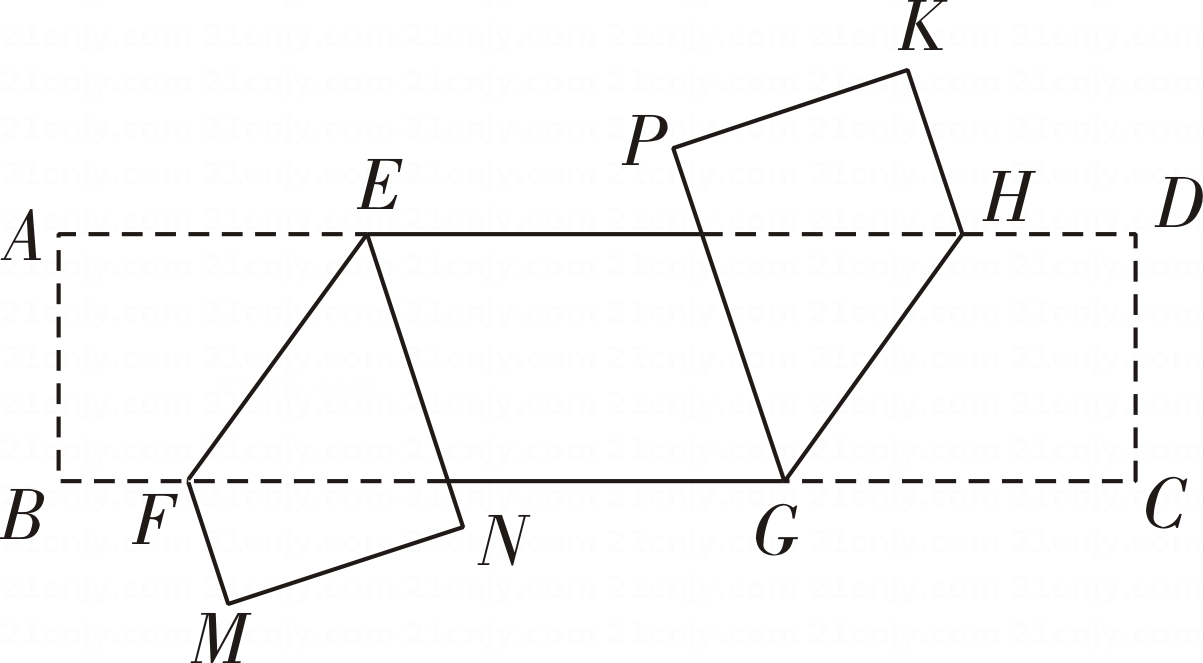

A、37°或143° B、74°或96° C、37°或105° D、74°或106°

查看试题解析

二、填空题

11. 如图，在 $△ A B C$ 中， $A B = A C$ ，将 $△ A B C$ 绕着点 $B$ 旋转后，点 $C$ 落在 $A C$ 边上的点 $E$ 处，点 $A$ 落在点 $D$ 处， $D E$ 与 $A B$ 相交于点 $F$ ，如果 $B E = B F$ ，那么 $∠ D B C$ 的大小是．

查看试题解析
12. 如图，四边形 $A B C D$ 是边长为5的正方形，E是 $D C$ 上一点， $D E = 1$ ，将 $△ A D E$ 绕着点A顺时针旋转到与 $△ A B F$ 重合，则 $E F =$ .

查看试题解析
13. 如图，一副三角板的三个内角分别是 $90 °$ ， $45 °$ ， $45 °$ 和 $90 °$ ， $60 °$ ， $30 °$ ，如图，若固定 $△ A B C$ ，将 $△ B D E$ 绕着公共顶点 $B$ 顺时针旋转 $α$ 度（ $0 < α < 180$ ），当边 $D E$ 与 $△ A B C$ 的某一边平行时，相应的旋转角 $α$ 的值为.

查看试题解析
14. 如图是一张矩形纸片ABCD，点E在边BC上，且满足 AB＝2BE，把△ABE沿直线AE折叠，使点B落在点F处，EF的延长线与边CD交于点G．若CG＝DG，则 $\frac{C E}{B E}$ ＝．

查看试题解析
15. 如图， $⊙ O$ 的半径为2 $c m$ ， $A B$ 为 $⊙ O$ 的弦，点C为 $\overset{⌢}{A B}$ 上的一点，将 $\overset{⌢}{A B}$ 沿弦 $A B$ 翻折，使点C与圆心O重合，则阴影部分的面积为.（结果保留π与根号）

查看试题解析
16. 如图，在 $▱ A B C D$ 中， $A C$ 与 $B D$ 相交于点O， $∠ A O B = 60 °$ ， $A C = 6$ ， $B D = 8$ ，将 $△ A B C$ 沿直线 $A C$ 翻折后，点B落在点E处，联结 $E A$ 、 $E D$ ，那么四边形 $A E D C$ 的周长 $=$ ．

查看试题解析

三、解答题

17. 如图，矩形纸片 $A B C D$ 中， $A B = 4 ， B C = 8$ ，将 $△ A B C$ 沿 $A C$ 折叠，使点 $B$ 落在点 $E$ 处， $C E$ 交 $A D$ 于点 $F$ ，求 $D F$ 的长．

查看试题解析
18. 如图，将矩形ABCD沿对角线AC折叠，点B的对应点为点E ， AE与CD交于点F ．

(1)、求证： $△ D A F ≌ △ E C F$ ；

(2)、若 $∠ F C E = 40 °$ ，求 $∠ C A B$ 的度数．

查看试题解析
19. 某数学活动小组在学完特殊的平行四边形之后，针对矩形中的折叠问题进行了研究．
如图 $①$ ，在矩形 $A B C D$ 中， $A B = 3 a$ ， $B C = 4 a$ ，点 $P$ 为 $A B$ 边上一点，将矩形 $A B C D$ 沿 $P C$ 折叠，点 $E$ 为点 $B$ 折叠后的对应点，过点 $E$ 作 $E F / / A B$ ，交折痕 $P C$ 于点 $F$ ，连接 $B F$ ．

(1)、猜想四边形 $P B F E$ 的形状，并证明你的结论；

(2)、如图 $②$ ，连接 $A C$ ，当点 $E$ 落在 $A C$ 上时， $B P$ 的长为 $($ 用含 $a$ 的代数式表示 $)$ ；

(3)、如图 $③$ ，当点 $E$ 落在 $A D$ 上时，若 $a = 2$ ，请直接写出 $A E$ 的长．

查看试题解析
20. 如图1，四边形ABCD是正方形，E，F分别在边BC和CD上，且∠EAF＝45°，我们把这种模型称为“半角模型”，在解决“半角模型”问题时，旋转是一种常用的方法。小明为了解决线段EF，BE，DF之间的关系，将△ADF绕点A顺时针旋转90°后解决了这个问题。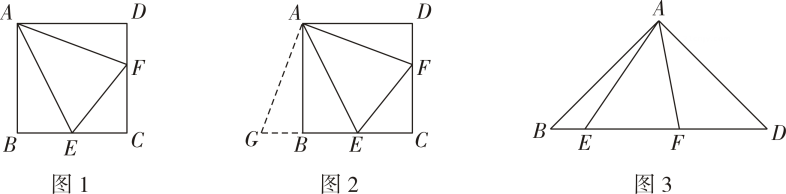

(1)、请直接写出线段EF，BE，DF之间的关系.

(2)、如图3，等腰直角三角形ABD，∠BAD=90°，AB=AD，点E，F在边BD上，且∠EAF=45°，请写出EF，BE，DF之间的关系，并说明理由.

查看试题解析

四、实践探究题

21.

(1)、【模型感知】如图①，在正方形ABCD中，点E是对角线AC上一点（不与点A、C重合），连接BE ，将线段BE绕点B逆时针旋转90°得到线段BE'，连接AE^' ，求证：AE'＝CE；

(2)、【模型发展】如图②，在正方形ABCD中，点E是对角线CA的延长线上的一点，连接BE ，将线段BE绕点B逆时针旋转90°得到线段BE'，连接AE'，线段AE^'与CE的数量关系为， AE'与CE所在直线的位置关系为（不需证明）；

(3)、【解决问题】如图③，在正方形ABCD中，点E是对角线AC延长线上的一点，连接BE ，将线段BE绕点B逆时针旋转90°，得到线段BE'，连接AE'，EE'，若AC＝3CE ，则 $\frac{S_{Δ A E E^{^{'}}}}{S_{Δ A B E}}$ ＝．

查看试题解析
22. 如图①．四边形ABCD与四边形AEFG是共一个顶点的两个大小不同的正方形．

(1)、操作发现：如图②．正方形AEFG绕顶点A逆时针旋转，使点E落在边AD上时．填空：
①线段BE与IG的数量关系是
②∠ABE与∠ADG的关系是

(2)、猜想与证明：如图③，正方形AEFG绕顶点A逆时针旋转某一角度α（0<α< 90°）时．猜想（1）中的结论是否成立？并证明你的结论：

(3)、拓展应用：如图④．正方形AEFG绕顶点A逆时针旋转，使点F落在边AD上时，若AB= $2 \sqrt{2}$ ． AF=1，则BE=

查看试题解析
23.

(1)、【性质探究】如图1，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ， AB＝AC ，点D在斜边BC上，将△ABD绕点A逆时针旋转90°得到△ACE．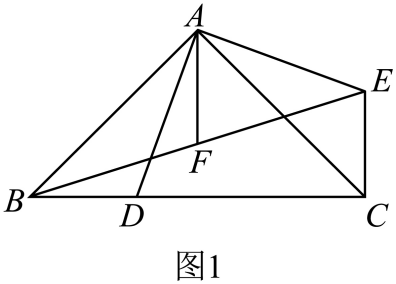
①直线BD与CE的位置关系为；
②若点F为BE的中点，连接AF ，请探究线段AF与CD的数量关系，并给予证明．

(2)、【拓展应用】
如图2，已知点E是正方形ABCD的边BC上任意一点，以AE为边作正方形AEFG ，连接BG，点H为BG的中点，连接AH ．若AB＝4，BE＝3，求AH的长．

查看试题解析
24. 综合与实践
问题背景：
数学课上，同学们以“长方形纸带的折叠”为主题开展数学活动，已知长方形纸带的边 $A D ∥ B C$ ， $A B ∥ C D$ ， $∠ A = ∠ B = ∠ C = ∠ D = 90 °$ ，点 $B^{'}$ 为线段AD上一动点 $(A B^{'} \geq A B)$ ，将纸片折叠，使点B和点 $B^{'}$ 重合，产生折痕EF，点E是折痕与边AD的交点，点F是折痕与边BC的交点．

动手操作：

(1)、如图1，若点E与点A重合时，则 $∠ A F B$ 的度数为．
实践探究：

(2)、如图2，移动点 $B^{'}$ ，其余条件不变．
①小静发现图中无论点 $B^{'}$ 如何移动， $∠ A^{'} E B^{'} = ∠ B^{'} F C$ 始终成立，请说明理由；
②小东发现折叠后所形成的角，只要知道其中一个角的度数，就能求出其它任意一角的度数，若 $∠ A^{'} B^{'} E = 60 °$ ，求 $∠ B^{'} E F$ 的大小．

查看试题解析

五、综合题

25. 如图，在平面直角坐标系中，A（－2，0），B（3，－1），C（2，2），网格中每一格的边长均为一个单位长度，请解答以下问题.

(1)、请在图中作出△ABC.

(2)、将△ABC平移，使得平移后点C的对应点为原点，点A、B的对应点分别为 $A_{1}$ ， $B_{1}$ ，请作出平移后的 $△ A_{1} B_{1} O$ ，并直接写出△ABC在CO方向上平移的距离.

(3)、将△ABC绕点A逆时针旋转90°，得到 $△ A B_{2} C_{2}$ ，点B、C的对应点分别为 $B_{2}$ 、 $C_{2}$ ，请作出 $△ A B_{2} C_{2}$ ，并直接写出点 $C_{2}$ ， $B_{2}$ 的坐标.

查看试题解析
26. 在 $▱ A B C D$ 中，∠ADC的平分线交直线BC于点E、交AB的延长线于点F，连接AC．

(1)、如图1，若∠ADC=90°，G是EF的中点，连接AG、CG.
①求证：BE=BF；
②请判断△AGC的形状，并说明理由.

(2)、如图2，若∠ADC=60°，将线段FB绕点F顺时针旋转60°至FG，连接AG、CG，判断△AGC的形状.（直接写出结论不必证明）

查看试题解析
27. 如图，在△ABC中，E是AB中点，F是AC上一动点，连结EF，将△AEF沿直线EF折叠得△DEF．

(1)、如图①，若∠B=45°，且点D恰好落在线段BC上，求证：点F为线段AC的中点；

(2)、如图②，若△ABC为等边三角形，且边长为4，当点D落在线段CE上时，求AF的长度；

(3)、如图③，若△ABC为直角三角形，∠BAC=90°，AC=8．连结AD、BD、CD，若△ACD与△BDC面积相等，且CD=4，求△ABC的面积．

查看试题解析
28. 如图，有一长方形纸带，E、F分别是边AD、BC上一点， $∠ D E F = α (0^{°} < α < 90^{°}$ 且 $α \neq 60^{°})$ ，将纸带ABCD沿EF折叠成图1，再沿GF折叠成图2.

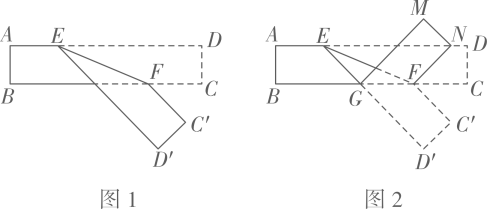
(1)、当οα=25时，则∠FGD'= ， ∠GFC'=；

(2)、两次折叠后，求∠NFE的大小（用含α的代数式表示）；

(3)、当∠NFE和∠DEF的度数之和为100°时，求α的值.

查看试题解析

2024年人教版中考数学二轮复习 专题18 图形的旋转、平移与轴对称

一、单选题

二、填空题

三、解答题

四、实践探究题

五、综合题

2024年人教版中考数学二轮复习专题18 图形的旋转、平移与轴对称