四川省巴中市巴州区2022-2023学年八年级下学期数学5月月考试题

试卷更新日期：2024-04-16 类型：月考试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 在□ABCD中， $∠ A ： ∠ B = 2 ： 3$ ，则 $∠ C$ 的度数为（）

A、 $36 °$ B、 $72 °$ C、 $108 °$ D、 $144 °$

查看试题解析
2. 平行四边形两邻边分别为 $24$ 和 $16$ ，则平行四边形的周长为（）

A、 $20$ B、 $40$ C、 $60$ D、 $80$

查看试题解析
3. 如图，▱ABCD的对角线AC，BD交于点O，已知AD=8，BD=12，AC=6，则△OBC的周长为（）

A、13 B、17 C、20 D、26

查看试题解析
4. 如图，四边形 $A B C D$ 中，对角线 $A C$ 、 $B D$ 相交于点 $O$ ，下列条件不能判定这个四边形是平行四边形的是（）

A、 $A B / / D C$ ， $A D / / B C$ B、 $A O = C O$ ， $B O = D O$ C、 $A B / / D C$ ， $A D = B C$ D、 $A B = D C$ ， $A D = B C$

查看试题解析
5. 顺次连接平面上 $A$ 、 $B$ 、 $C$ 、 $D$ 四点得到一个四边形，从 $① A B / / C D ； ② B C = A D ； ③ ∠ A = ∠ C ； ④ ∠ B = ∠ D$ 四个条件中任取其中两个，可以得出“四边形 $A B C D$ 是平行四边形”这一结论的情况共有（）

A、 $5$ 种 B、 $4$ 种 C、 $3$ 种 D、 $1$ 种

查看试题解析
6. 如图，点 $E$ ， $F$ 是平行四边形 $A B C D$ 对角线 $B D$ 上两点，顺次连接 $A$ ， $E$ ， $C$ ， $F$ 得到四边形 $A E C F$ ，添加下列条件不一定能得到四边形 $A E C F$ 是平行四边形的是（）

A、 $B E = D F$ B、 $A E / / C F$ C、 $A E = C F$ D、 $∠ A E B = ∠ C F D$

查看试题解析
7. 如图，在▱ABCD中，延长AB到点E，使BE=AB，连接DE交BC于点F，则下列结论不一定成立的是（）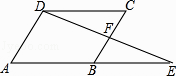

A、∠E=∠CDF B、EF=DF C、AD=2BF D、BE=2CF

查看试题解析
8. 如图，在▱ABCD中，BE平分∠ABC交AD于点E，CF平分∠BCD交AD于点F，AB＝3，AD＝5，则EF的长为(　　)

A、1 B、1.5 C、2 D、2.5

查看试题解析
9. 如图，在平行四边形 $A B C D$ 中， $A E ⊥ B C$ 于E， $A F ⊥ C D$ 于F，若 $A E = 4 ， A F = 6$ ，平行四边形 $A B C D$ 的周长为40，则平行四边形 $A B C D$ 的面积为（）

A、48 B、24 C、36 D、60

查看试题解析
10. 如图，点E在平行四边形ABCD内部， $A F ∥ B E$ ， $D F ∥ C E$ ，设平行四边形ABCD的面积为 $S_{1}$ ，四边形AEDF的面积为 $S_{2}$ ，则 $\frac{S_{1}}{S_{2}}$ 的值是（）

A、 $\frac{2}{3}$ B、 $\frac{3}{2}$ C、1 D、2

查看试题解析

二、填空题（每题3分，共18分）

11. 如图，在四边形 $A B C D$ 中， $A D = B C$ ，在不添加任何辅助线的情况下，请你添加一个条件，使四边形 $A B C D$ 是平行四边形．

查看试题解析
12. 已知平行四边形ABCD中，∠B＋∠D＝270°，则∠C＝．

查看试题解析
13. 下列给出的条件中，不能判定四边形 $A B C D$ 是平行四边形的为 $($ 填序号 $)$ ．
$① A B = C D$ ， $A D = B C$ ； $② A D = B C$ ， $A D / / B C$ ；
$③ A B = C D$ ， $∠ B = ∠ D$ ； $④ A B / / C D$ ， $∠ A = ∠ C$ ．

查看试题解析
14. 如图，已知平行四边形 $A B C D$ 的周长是 $26 c m$ ， $A C$ 和 $B D$ 相交于点 $O$ ， $△ O B C$ 的周长比 $△ O A B$ 的周长小 $2 c m$ ，那么 $A D =$ $c m$ ．

查看试题解析
15. 如图， $E$ 是平行四边形 $A B C D$ 边 $B C$ 上的一点，且 $A B$ ＝ $B E$ ，连接 $A E$ ， $A E$ 的延长线与 $D C$ 的延长线交于点 $F$ 。若 $∠ F$ ＝ $70^{\circ}$ ，则 $∠ D$ ＝.

查看试题解析
16. 如图，在四边形 $A B C D$ 中， $A D / / B C$ ，且 $A D = 8 c m$ ， $B C = 6 c m$ ，点 $P$ ， $Q$ 分别从点 $A$ ， $C$ 同时出发，点 $P$ 以 $1 c m / s$ 的速度由点 $A$ 向点 $D$ 运动，点 $Q$ 以 $2 c m / s$ 的速度由点 $C$ 向点 $B$ 运动，当点 $P$ ， $Q$ 中有一点到达终点时，另一点也随之停止运动，则 $s$ 后四边形 $P Q C D$ 是平行四边形．

查看试题解析

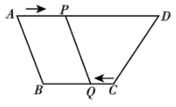
三、解答题

17. 如图，已知四边形ABCD是平行四边形，BE⊥AC， DF⊥AC，求证：AE＝CF．

查看试题解析
18. 如图，四边形ABCD是平行四边形，延长BA至点E，使AE＋CD＝AD，连接CE.求证：CE平分∠BCD.

查看试题解析
19. 如图，▱ABCD中，DF平分∠ADC，交BC于点F，BE平分∠ABC，交AD于点E．

(1)、求证：四边形BFDE是平行四边形；

(2)、若∠AEB=68°，求∠C．

查看试题解析
20. 如图，在 $▱ O A B C$ 中，点O为坐标顶点，点 $A (3 ， 0)$ ， $C (1 ， 2)$ ，反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象经过点C．

(1)、求k的值及直线OB的函数表达式；

(2)、试探究此反比例函数的图象是否经过 $▱ O A B C$ 的中心．

查看试题解析
21. 如图所示，▱ABCD的边AB在x轴上，点D在y轴上，已知OA＝3，AD＝6，BD⊥AD ，从C点出发的点E ，以每秒1个单位的速度向点D移动．M是BD的中点，EM的延长线交AB于点F ．

(1)、求点B ， C的坐标；

(2)、当四边形EFBC是平行四边形时，求点E的移动时间t（秒）．

(3)、当△DEM为等腰三角形时，求CE的长．

查看试题解析