四川省自贡市2022-2023学年八年级下学期5月月考数学试卷
试卷更新日期:2024-04-16 类型:月考试卷
一、选择题
-
1. 不等式>0的最大整数解是( )A、3 B、4 C、5 D、62. 一次函数 的图象大致是( )A、
 B、
B、 C、
C、 D、
D、 3. 如果 , 下列不等式不一定成立的是( )A、 B、 C、 D、4. 不等式组的解集在数轴上表示为( ).A、
3. 如果 , 下列不等式不一定成立的是( )A、 B、 C、 D、4. 不等式组的解集在数轴上表示为( ).A、 B、
B、 C、
C、 D、
D、 5. 如图,RtABC中,∠ACB=90°,CD是高,∠A=30°,CD= cm则AB的长为( )
5. 如图,RtABC中,∠ACB=90°,CD是高,∠A=30°,CD= cm则AB的长为( ) A、4cm B、6cm C、8cm D、10cm6. 如图所示,△ABC的顶点A,B,C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为( )
A、4cm B、6cm C、8cm D、10cm6. 如图所示,△ABC的顶点A,B,C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为( ) A、 B、 C、 D、7. 如图,菱形 的边长是5,O是两条对角线的交点,过O点的三条直线将菱形分成阴影部分和空白部分,若菱形的一条对角线的长为4,则阴影部分的面积为( )
A、 B、 C、 D、7. 如图,菱形 的边长是5,O是两条对角线的交点,过O点的三条直线将菱形分成阴影部分和空白部分,若菱形的一条对角线的长为4,则阴影部分的面积为( )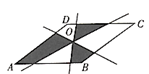 A、 B、 C、12 D、248. 如图,一次函数 的图象与直线 相交于点 (-1,3),则关于 的不等式 的解集为 ( )
A、 B、 C、12 D、248. 如图,一次函数 的图象与直线 相交于点 (-1,3),则关于 的不等式 的解集为 ( ) A、 B、 C、 D、9. 已知正比例函数y=(3k-1)x的图象经过第一、三象限,则k的取值范围是( )A、k>0 B、k<0 C、 D、10. 为弘扬传统文化,某校初二年级举办传统文化进校园朗诵大赛,小明同学根据比赛中九位评委所给的某位参赛选手的分数,制作了一个表格,如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
A、 B、 C、 D、9. 已知正比例函数y=(3k-1)x的图象经过第一、三象限,则k的取值范围是( )A、k>0 B、k<0 C、 D、10. 为弘扬传统文化,某校初二年级举办传统文化进校园朗诵大赛,小明同学根据比赛中九位评委所给的某位参赛选手的分数,制作了一个表格,如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )中位数
众数
平均数
方差
9.2
9.3
9.1
0.3
A、中位数 B、众数 C、平均数 D、方差11. 已知关于x的不等式组 至多有3个整数解,且关于x的分式方程=﹣2的解为非负数,则符合条件的所有整数a的和为( )A、﹣15 B、﹣12 C、﹣9 D、﹣712. 如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为( )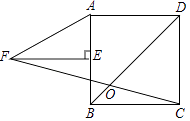 A、60° B、67.5° C、75° D、54°
A、60° B、67.5° C、75° D、54°二、填空题
-
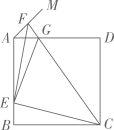
13. 如果直角三角形的两条直角边长分别为a , b , 斜边长为c , 那么 .14. 已知一次函数(为常数)和 . 当时,;当时. , 则的值为 .15. 如图,正方形ABCD的边长为a,点E在边AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且 ,CF与AD相交于点G,连接EC,EF,EG,则下列结论:①∠ECF=45°;② 的周长为 ;③ ;④ 的面积的最大值 .其中正确的结论是.(填写所有正确结论的序号)
 16. 如图,在中, , , , 则的长是 .
16. 如图,在中, , , , 则的长是 . 17. 如图,正方形的边长是10,点E在边上,点F是边上, , 把沿折叠,点B落在处.若恰为等腰三角形,则的长为 .
17. 如图,正方形的边长是10,点E在边上,点F是边上, , 把沿折叠,点B落在处.若恰为等腰三角形,则的长为 . 18. 解不等式组
18. 解不等式组请结合解题过程,完成本题的解答.
⑴解不等式①,得;
⑵解不等式②,得;
⑶把不等式①和②的解集在数轴上表示出来:

⑷原不等式组的解集为 .
三、解答题
-
19. 图、图是两张形状、大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,点、在小正方形的顶点上.
 (1)、在图中画出(点在小正方形的顶点上),使为轴对称图形;(2)、在图中画出四边形(点、都在小正方形的顶点上),使四边形面积为3的轴对称图形.20. 已知如图,直线与y轴交于A(0,6),直线分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.求:
(1)、在图中画出(点在小正方形的顶点上),使为轴对称图形;(2)、在图中画出四边形(点、都在小正方形的顶点上),使四边形面积为3的轴对称图形.20. 已知如图,直线与y轴交于A(0,6),直线分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.求: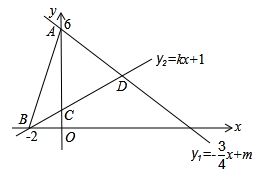 (1)、直线的解析式;(2)、求△ABD的面积;(3)、在x轴上是否存在一点P,使得 , 若存在,求出点P的坐标;若不存在,说明理由.21. 已知:如图,直线l是一次函数 的图象 求:
(1)、直线的解析式;(2)、求△ABD的面积;(3)、在x轴上是否存在一点P,使得 , 若存在,求出点P的坐标;若不存在,说明理由.21. 已知:如图,直线l是一次函数 的图象 求: (1)、这个函数的解析式;(2)、当 时,y的值.22. 某数学活动小组在研究三角形拓展图形的性质时,经历了如下过程:
(1)、这个函数的解析式;(2)、当 时,y的值.22. 某数学活动小组在研究三角形拓展图形的性质时,经历了如下过程: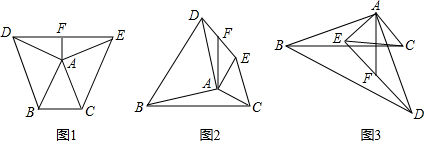 (1)、●操作发现
(1)、●操作发现在等腰△ABC中,AB=AC , 分别以AB和AC为腰,向△ABC的外侧作等腰直角三角形,如图①所示,连接DE , 其中F是DE的中点,连接AF , 则下列结论正确的是(填序号即可)
①AF=BC:②AF⊥BC;③整个图形是轴对称图形;④DE∥BC、
(2)、●数学思考在任意△ABC中,分别以AB和AC为腰,向△ABC的外侧作等腰直角三角形,如图②所示,连接DE , 其中F是DE的中点,连接AF , 则AF和BC有怎样的数量和位置关系?请给出证明过程
(3)、●类比探索在任意△ABC中,仍分别以AB和AC为腰,向△ABC的内侧作等腰直角三角形,如图③所示,连接DE , 其中F是DE的中点,连接AF , 试判断AF和BC的数量和位置关系是否发生改变?并说明理由.