四川省成都市锦江区重点学校2023-2024学年七年级上学期数学期末考试试卷
试卷更新日期:2024-04-16 类型:期末考试
一、选择题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 如图是由6个完全相同的小正方体组成的几何体,其俯视图为( )
 A、
A、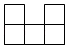 B、
B、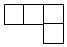 C、
C、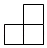 D、
D、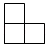 3. 据统计我国每年浪费的粮食约35000000吨,我们要勤俭节约,反对浪费,积极的加入“光盘行动”中来.用科学记数法表示35000000是( ).A、3.5×106 B、3.5×107 C、35×106 D、35×1074. 已知 , , 且 , 则的值等于( )A、或 B、或 C、或 D、或5. 某班将安全知识竞赛成绩整理后绘制成如图所示的频数分布直方图每组不包括最小值,包括最大值 , 图中从左至右前四组的频数占总人数的百分比分别为 , , , , 且第五组的频数是 , 下列结论不正确的是( )
3. 据统计我国每年浪费的粮食约35000000吨,我们要勤俭节约,反对浪费,积极的加入“光盘行动”中来.用科学记数法表示35000000是( ).A、3.5×106 B、3.5×107 C、35×106 D、35×1074. 已知 , , 且 , 则的值等于( )A、或 B、或 C、或 D、或5. 某班将安全知识竞赛成绩整理后绘制成如图所示的频数分布直方图每组不包括最小值,包括最大值 , 图中从左至右前四组的频数占总人数的百分比分别为 , , , , 且第五组的频数是 , 下列结论不正确的是( )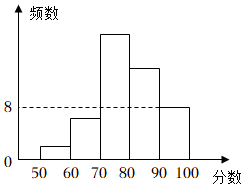 A、第五组的频数占总人数的百分比为 B、该班有名同学参赛 C、成绩在分的人数最多 D、分以上的学生有名6. 下列说法不正确的是( )A、一个次数是的多项式中,各项的次数都不大于 B、代数式表示 , 两数的平方差 C、是三次三项式 D、若 , 则7. 九章算术中有这样一道数学问题,原文如下:清明游园,共坐八船,大船满六,小船满四,三十八学子,满船坐观请问客家,大小几船?其大意为:清明时节出去游园,所有人共坐了只船,大船每只坐人,小船每只坐人,人刚好坐满,问:大小船各有几只?若设有只小船,则可列方程为( )A、 B、 C、 D、8. 在数轴上,点A对应的数是-6,点B对应的数是-2,点O对应的数是0.动点P、Q分别从A、B同时出发,以每秒3个单位,每秒1个单位的速度向右运动。在运动过程中,线段PQ的长度始终是另一线段长的整数倍,这条线段是( )
A、第五组的频数占总人数的百分比为 B、该班有名同学参赛 C、成绩在分的人数最多 D、分以上的学生有名6. 下列说法不正确的是( )A、一个次数是的多项式中,各项的次数都不大于 B、代数式表示 , 两数的平方差 C、是三次三项式 D、若 , 则7. 九章算术中有这样一道数学问题,原文如下:清明游园,共坐八船,大船满六,小船满四,三十八学子,满船坐观请问客家,大小几船?其大意为:清明时节出去游园,所有人共坐了只船,大船每只坐人,小船每只坐人,人刚好坐满,问:大小船各有几只?若设有只小船,则可列方程为( )A、 B、 C、 D、8. 在数轴上,点A对应的数是-6,点B对应的数是-2,点O对应的数是0.动点P、Q分别从A、B同时出发,以每秒3个单位,每秒1个单位的速度向右运动。在运动过程中,线段PQ的长度始终是另一线段长的整数倍,这条线段是( ) A、PB B、OP C、OQ D、QB
A、PB B、OP C、OQ D、QB二、非选择题
-
9. 若与是同类项,则 .10. 如图是一个正方体的平面展开图,若将其按虚线折叠成正方体后,相对面上的两个数字之和均为 , 则 .
 11. 过多边形的一个顶点的所有对角线把多边形分成个三角形,这个多边形的边数是 .12. 已知: , , 的值为 .13. A,B,C三点在同一直线上,线段AB=5cm,BC=4cm,那么A,C两点的距离是.14. 计算:
11. 过多边形的一个顶点的所有对角线把多边形分成个三角形,这个多边形的边数是 .12. 已知: , , 的值为 .13. A,B,C三点在同一直线上,线段AB=5cm,BC=4cm,那么A,C两点的距离是.14. 计算:
(1)、;
(2)、;
(3)、;(4)、解方程 .15. 先化简,再求值: , 其中 , .16. 4月23日是世界读书日.为了解学生的阅读喜好,丰富学校图书资源,某校将课外书籍设置了四类:文学类、科技类、艺术类、其他类,随机抽查了部分学生,要求每名学生从中选择自己最喜欢的一类,将抽查结果绘制成如图统计图(不完整).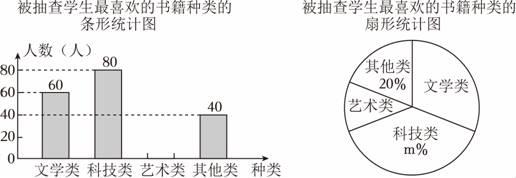
请根据图中信息解答下列问题:
(1)、求被抽查的学生人数,并求出扇形统计图中m的值.(2)、请将条形统计图补充完整.(温馨提示:请画在答题卷相对应的图上)(3)、若该校共有1200名学生,根据抽查结果,试估计全校最喜欢“文学类”书籍的学生人数.17. 定义 , 如已知为常数 , .(1)、若 , 则的值为;(2)、若的代数式中不含的一次项,当时,求的值;(3)、若中的满足时,且 , 求的值.18. 如图 , 线段在线段上运动,、分别是、的中点.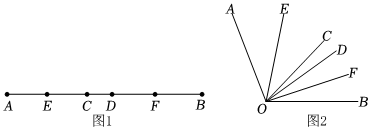 (1)、若线段 , , 求的长.(2)、若 , , 由此可以猜想用、表示 .(3)、我们发现角的很多规律和线段一样:如图 , 绕点逆时针旋转初始位置、重合,旋转度数 , 、分别平分和 , 若 , , 在旋转过程中,的大小是否为定值?若是,请求出该值;若不是,请说明理由.19. 已知x2-2(m+3)x+9是一个完全平方式,则m= .20. 有理数、、在数轴上的位置如图,则的化简结果为 .
(1)、若线段 , , 求的长.(2)、若 , , 由此可以猜想用、表示 .(3)、我们发现角的很多规律和线段一样:如图 , 绕点逆时针旋转初始位置、重合,旋转度数 , 、分别平分和 , 若 , , 在旋转过程中,的大小是否为定值?若是,请求出该值;若不是,请说明理由.19. 已知x2-2(m+3)x+9是一个完全平方式,则m= .20. 有理数、、在数轴上的位置如图,则的化简结果为 . 21. 若关于的方程的解是整数,且关于的多项式是二次三项式,则满足条件的整数的值是 .22. 已知 , , , 按此规律,则 .23. 定义:是以、、为系数的二次多项式,即 , 其中、、均为实数例如、 .
21. 若关于的方程的解是整数,且关于的多项式是二次三项式,则满足条件的整数的值是 .22. 已知 , , , 按此规律,则 .23. 定义:是以、、为系数的二次多项式,即 , 其中、、均为实数例如、 .
当时,求;
若 , 求 .24. 为了迎接新学期,书店计划购进、两类书刊,且书刊和书刊的售价分别是元本和元本,且书刊的进价比书刊贵元已知购买本书刊和本书刊共需要元.(1)、求、两类书刊的进价各是多少元?(2)、若该书店第一次购进、两类书刊共本,全部售完后总利润为元,求该书店第一次分别购进、两类书刊各多少本?(3)、若第二次购进同样数量的两类书刊,且两类书刊的进价都比上次优惠了 , 再次销售时类书刊售价不变,类书刊打折出售,全部售完后总利润比上次还多元,求类书刊打了几折?25. (1)、【教材重现】如图 , 边长为的大正方形中有一个边长为的小正方形,把图中的阴影部分拼成一个长方形如图所示 .
(1)、【教材重现】如图 , 边长为的大正方形中有一个边长为的小正方形,把图中的阴影部分拼成一个长方形如图所示 .
上述操作能验证的公式是 .
(2)、【类比探究】把上述两个正方形按照如图所示的方式拼接,其中 , , 三点在同一直线上若 , , 求阴影部分的面积.
(3)、【拓展应用】根据前面的经验探究:若满足 , 求的值.26. 若一个角是另一个角的二倍,则称这两个角互为“共轭角”.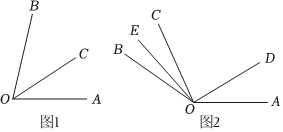 (1)、已知且和互为“共轭角”,则 ;(2)、如图 , , 是内部的一条射线,若图中存在“共轭角”,试求出的度数;(3)、如图 , , , 射线从绕点逆时针旋转,速度为每秒,到停止运动;射线以每秒的速度从顺时针旋转到 , 再以每秒的速度逆时针返回 , 射线按照这种方式在内部往返,并随停止而停止二者同时出发,设运动时间为秒,在这一过程中,若和互为“共轭角”,求的值.
(1)、已知且和互为“共轭角”,则 ;(2)、如图 , , 是内部的一条射线,若图中存在“共轭角”,试求出的度数;(3)、如图 , , , 射线从绕点逆时针旋转,速度为每秒,到停止运动;射线以每秒的速度从顺时针旋转到 , 再以每秒的速度逆时针返回 , 射线按照这种方式在内部往返,并随停止而停止二者同时出发,设运动时间为秒,在这一过程中,若和互为“共轭角”,求的值.