重庆市万州区2024年中考数学重难点检测卷
试卷更新日期:2024-04-16 类型:中考模拟
一、单选题
-
1. 9的相反数是( )A、 B、 C、9 D、2. 如图,由5个相同正方体组合而成的几何体,它的俯视图是( )
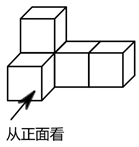 A、
A、 B、
B、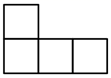 C、
C、 D、
D、 3. 如图, , , 则( )
3. 如图, , , 则( ) A、 B、 C、 D、4. 反比例函数的图象过(3,6),则k的值为( )A、15 B、18 C、21 D、255. 如图,和是位似图形,点是位似中心,若 , 的面积为 , 则的面积为( )
A、 B、 C、 D、4. 反比例函数的图象过(3,6),则k的值为( )A、15 B、18 C、21 D、255. 如图,和是位似图形,点是位似中心,若 , 的面积为 , 则的面积为( ) A、1 B、 C、 D、6. 如图,每个图形都由同样大小的“△”按照一定的规律组成,其中第1个图形有5个“△”,第2个图形有10个“△”,第3个图形有15个“△”,…,则第8个图形中“△”的个数为( )
A、1 B、 C、 D、6. 如图,每个图形都由同样大小的“△”按照一定的规律组成,其中第1个图形有5个“△”,第2个图形有10个“△”,第3个图形有15个“△”,…,则第8个图形中“△”的个数为( )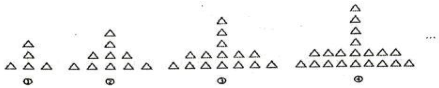 A、40 B、42 C、44 D、467. 估计的值应为( )A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间8. 如图,在矩形中,E、F为AC上一点, , , 连接、 , 若 , 则的度数为( )
A、40 B、42 C、44 D、467. 估计的值应为( )A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间8. 如图,在矩形中,E、F为AC上一点, , , 连接、 , 若 , 则的度数为( ) A、 B、 C、 D、9. 如图,是的直径,为上一点,连接 , 于点 , 是的切线,且 , 若 , , 则的长为( )
A、 B、 C、 D、9. 如图,是的直径,为上一点,连接 , 于点 , 是的切线,且 , 若 , , 则的长为( ) A、 B、4 C、 D、10. 在多项式中,除首尾项a、外,其余各项都可闪退,闪退项的前面部分和其后面部分都加上绝对值,并用减号连接,则称此为“闪减操作”.每种“闪减操作”可以闪退的项数分别为一项,两项,三项.“闪减操作”只针对多项式进行.例如:“闪减操作”为 , 与同时“闪减操作”为 , …,下列说法:
A、 B、4 C、 D、10. 在多项式中,除首尾项a、外,其余各项都可闪退,闪退项的前面部分和其后面部分都加上绝对值,并用减号连接,则称此为“闪减操作”.每种“闪减操作”可以闪退的项数分别为一项,两项,三项.“闪减操作”只针对多项式进行.例如:“闪减操作”为 , 与同时“闪减操作”为 , …,下列说法:①存在对两种不同的“闪减操作”后的式子作差,结果不含与e相关的项;②若每种操作只闪退一项,则对三种不同“闪减操作”的结果进行去绝对值,共有8种不同的结果;③若可以闪退的三项 , , 满足:
, 则的最小值为 .
其中正确的个数是( )
A、0 B、1 C、2 D、3二、填空题
-
11. 二次根式中,x的取值范围是 .12. 计算:= .13. 某校为迎接全国“创文创未”检查工作,从3名教师(其中,2男1女)中随机选择两名教师负责协调全国“创文创未”的相关检查工作,则恰好选中1名男教师和1名女教师的概率为 .14. 如图,在菱形中, , , 反比例函数的图象经过边的中点,则反比例函数的解析式为 .
 15. 如图,在矩形中, , , 以点A为圆心,长为半径画弧,交于点E , 则图中阴影部分的面积是 . (结果不取近似值)
15. 如图,在矩形中, , , 以点A为圆心,长为半径画弧,交于点E , 则图中阴影部分的面积是 . (结果不取近似值) 16. 如图,在中, , , D是边上一点(点D不与A、B重合).将沿着翻折,点B的对应点为点E , 交于点F , 如果 , 则 .
16. 如图,在中, , , D是边上一点(点D不与A、B重合).将沿着翻折,点B的对应点为点E , 交于点F , 如果 , 则 . 17. 若关于x的一元一次不等式组的解集为 , 且关于y的分式方程的解是正整数,则所有满足条件的整数a的值之和是 .18. 对于一个四位自然数N ,其千位数字为a , 百位数字为b ,十位数字为c , 个位数字为d , 各个数位上的数字均不相同且均不为0.将自然数N的千位数字和个位数字组成一个两位数 , 记为A;百位数字和十位数字组成另一个两位数字 , 记为B , 若A与B的和等于N的千位数字与百位数字之和的11倍,则称N为“坎数”.例如:6345, , , , , 所以6345是“坎数”.若N为“坎数”,且 , 当为9的倍数时,则所有満足条件的N的最大值为 .
17. 若关于x的一元一次不等式组的解集为 , 且关于y的分式方程的解是正整数,则所有满足条件的整数a的值之和是 .18. 对于一个四位自然数N ,其千位数字为a , 百位数字为b ,十位数字为c , 个位数字为d , 各个数位上的数字均不相同且均不为0.将自然数N的千位数字和个位数字组成一个两位数 , 记为A;百位数字和十位数字组成另一个两位数字 , 记为B , 若A与B的和等于N的千位数字与百位数字之和的11倍,则称N为“坎数”.例如:6345, , , , , 所以6345是“坎数”.若N为“坎数”,且 , 当为9的倍数时,则所有満足条件的N的最大值为 .三、解答题
-
19. 计算:(1)、(2)、20. 在学习角平分线的过程中,小琦遇到了这样一个问题:在梯形中, , 若平分 , 且点E是边的中点,则.他的思路是:过点E作的垂线,将其转化为证明三角形全等,进行转边,从而解决问题.请根据小琦的思路完成下面的作图与填空:
证明:用直尺和圆规,过点E作于点F(保留作图痕迹)
平分 ,
∴ ①
又
∴ ② (
,
∵点E是的中点,
,
在与中
,
③
 21. 某校为提高学生对地震灾害的自救意识,开展了关于地震自救知识的竞赛,现从该校七、八年级中各抽取20名学生的竞赛成绩(百分制)进行整理、描述和分析(x表示竞赛成绩,x取整数):A.;B.;C.;D. , 下面给出了部分信息:
21. 某校为提高学生对地震灾害的自救意识,开展了关于地震自救知识的竞赛,现从该校七、八年级中各抽取20名学生的竞赛成绩(百分制)进行整理、描述和分析(x表示竞赛成绩,x取整数):A.;B.;C.;D. , 下面给出了部分信息:七年级抽取20名学生的竞赛成绩在B组中的数据为:90,91,92,92,93,93,94八年级抽取20名同学竞赛成绩数据为:80,85,82,81,88,86,92,88,92,93,97,94,100,96,99,96,93,97,96,95.

七、八年级抽取的学生竞赛成绩统计表
年级
平均分
中位数
众数
七年级
91.5
b
93
八年级
91.5
93
c
请根据相关信息,回答以下问题:
(1)、直接写出a , b , c的值,并补全八年级抽取的学生竞赛成绩条形统计图;(2)、根据以上数据,你认为该校七、八年级中哪个年级学生掌握地震自救知识较好?请说明理由(写一条理由即可);(3)、该校七年级有1000人,八年级有1200人参加了此次竞赛活动,请估计参加此次竞赛活动成绩优秀()的学生人数是多少?22. 如图1,在等腰中, , , D为底边的中点,点P从A点出发以每秒1个单位长度的速度向终点B运动,动点Q从C点出发,以每秒2个单位长度的速度;沿着的路线运动,设运动时间为t , 连接 , , , 记的面积为 , 记的面积为 , 请解答下列问题: (1)、请直接写出 , 与t之间的函数关系式以及对应的t的取值范围;并在如图2所示的平面直角坐标系中分别画出 , 的函数图象;(2)、观察的函数图象,写出函数的一条性质;(3)、根据图象,直接写出当时,t的取值范围.23. 重庆市潼南区是中国西部绿色菜都,为全市人民提供了新鲜多样的蔬菜.今年,区政府着力打造一个新的蔬菜基地,计划修建灌溉水渠1920米,由甲、乙两个施工队合作完成.已知乙施工队每天修建的长度是甲施工队每天修建的长度的 , 而乙施工队单独修建这项工程需要的天数比甲施工队单独修建这项工程需要的天数少4天.(1)、求甲、乙两施工队每天各修建多少米?(2)、若甲施工队每天的修建费用为13万元,乙施工队每天的修建费用为15万元,实际修建时先由甲施工队单独修建若干天,再由甲、乙两个施工队合作修建,恰好12天完成修建任务,求共需修建费用多少万元?24. 如图,在小晴家所住的高楼的正西方有一座小山坡,坡面与水平面的夹角为 , 在B点处测得楼顶D的仰角为 , 在山顶C处测得楼顶D的仰角为 , B和C的水平距离为300米.(A , B , C , D在同一平面内,参考数据: , )
(1)、请直接写出 , 与t之间的函数关系式以及对应的t的取值范围;并在如图2所示的平面直角坐标系中分别画出 , 的函数图象;(2)、观察的函数图象,写出函数的一条性质;(3)、根据图象,直接写出当时,t的取值范围.23. 重庆市潼南区是中国西部绿色菜都,为全市人民提供了新鲜多样的蔬菜.今年,区政府着力打造一个新的蔬菜基地,计划修建灌溉水渠1920米,由甲、乙两个施工队合作完成.已知乙施工队每天修建的长度是甲施工队每天修建的长度的 , 而乙施工队单独修建这项工程需要的天数比甲施工队单独修建这项工程需要的天数少4天.(1)、求甲、乙两施工队每天各修建多少米?(2)、若甲施工队每天的修建费用为13万元,乙施工队每天的修建费用为15万元,实际修建时先由甲施工队单独修建若干天,再由甲、乙两个施工队合作修建,恰好12天完成修建任务,求共需修建费用多少万元?24. 如图,在小晴家所住的高楼的正西方有一座小山坡,坡面与水平面的夹角为 , 在B点处测得楼顶D的仰角为 , 在山顶C处测得楼顶D的仰角为 , B和C的水平距离为300米.(A , B , C , D在同一平面内,参考数据: , ) (1)、求坡面的长度?(结果保留根号)(2)、一天傍晚,小晴从A出发去山顶C散步,已知小晴从A到B的速度为每分钟50米,从B沿着上山的速度为每分钟25米,若她出发,请通过计算说明她在前能否到达山顶C处?(结果精确到0.1)25. 已知抛物线与x轴交于A、B两点(A点在B点左侧),与y轴交于点C , 且 , 该抛物线的对称轴为直线 .
(1)、求坡面的长度?(结果保留根号)(2)、一天傍晚,小晴从A出发去山顶C散步,已知小晴从A到B的速度为每分钟50米,从B沿着上山的速度为每分钟25米,若她出发,请通过计算说明她在前能否到达山顶C处?(结果精确到0.1)25. 已知抛物线与x轴交于A、B两点(A点在B点左侧),与y轴交于点C , 且 , 该抛物线的对称轴为直线 . (1)、求该抛物线的解析式;(2)、如图1,E为直线下方抛物线上一点,过点E作轴交直线于点F , 求的最大值及此时点E的坐标;(3)、将该抛物线沿射线方向平移个单位,得到新的抛物线 , M为与y轴的交点,N为新抛物线对称轴上一点,点C平移后的对应点为Q , 平面内是否存在点P , 使得以M、N、P、Q为顶点的四边形为矩形,若存在请写出所有点P的坐标,并写出其中一种情况的过程;若不存在请说明理由.26. 如图,是等边三角形,D为上一点,连接 , 将绕点C顺时针旋转120°至 , 连接 , 分别交、于点F、G.
(1)、求该抛物线的解析式;(2)、如图1,E为直线下方抛物线上一点,过点E作轴交直线于点F , 求的最大值及此时点E的坐标;(3)、将该抛物线沿射线方向平移个单位,得到新的抛物线 , M为与y轴的交点,N为新抛物线对称轴上一点,点C平移后的对应点为Q , 平面内是否存在点P , 使得以M、N、P、Q为顶点的四边形为矩形,若存在请写出所有点P的坐标,并写出其中一种情况的过程;若不存在请说明理由.26. 如图,是等边三角形,D为上一点,连接 , 将绕点C顺时针旋转120°至 , 连接 , 分别交、于点F、G. (1)、若 , , 求的面积;(2)、请猜想线段 , , 之间的数量关系,并证明你的猜想;(3)、当周长最小时,请直接写出的值.
(1)、若 , , 求的面积;(2)、请猜想线段 , , 之间的数量关系,并证明你的猜想;(3)、当周长最小时,请直接写出的值.