云南省玉溪市红塔区2023-2024学年九年级上学期期末数学试题

试卷更新日期：2024-04-16 类型：期末考试

进入出卷网下载

一、选择题（本大题共12小题，每小题只有一个正确选项，每小题3分，满分36分）

1. “龙马腾霄绝胜景，山中深藏白玉城”，冬日某一天的龙马山，山脚最低气温为零上 $3 ℃$ ，记作 $+ 3 ℃$ ，山顶最低气温为零下 $2 ℃$ ，可记作（）

A、 $2 ℃$ B、 $+ 3 ℃$ C、 $- 2 ℃$ D、 $- 3 ℃$

查看试题解析
2. 如图，已知直线 $c$ 与直线 $a ， b$ 都相交．若 $a ∥ b ， ∠ 1 = 45 °$ ，则 $∠ 2 =$ （）

A、 $145 °$ B、 $135 °$ C、 $55 °$ D、 $45 °$

查看试题解析
3. 下列运算正确的是（）

A、 $202 4^{0} = 0$ B、 $\sqrt{4} = 2 \sqrt{2}$ C、 $(- 3 a)^{2} = - 6 a^{2}$ D、 $2 b^{2} - 3 b^{2} = - b^{2}$

查看试题解析
4. 函数 $y = \frac{x^{2}}{x - 4}$ 的自变量 $x$ 的取值范围为（）

A、 $x \geq 4$ B、 $x \neq 4$ C、 $x \geq 0$ 且 $x \neq 4$ D、任意实数

查看试题解析
5. 一元二次方程 $x^{2} - 3 x + 3 = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能判定

查看试题解析
6. 下列汉字中，可以看作是中心对称图形的是（）

A、知 B、行 C、合 D、一

查看试题解析
7. 如图，点 $A ， B ， C$ 在 $⊙ O$ 上，若 $∠ B A C = 55 °$ ，则 $∠ B O C$ 的度数是（）

A、 $55 °$ B、 $66 °$ C、 $110 °$ D、 $120 °$

查看试题解析
8. 按一定规律排列的单项式： $\sqrt{2} x^{2} ， 2 x^{2} ， \sqrt{6} x^{2} ， 2 \sqrt{2} x^{2} ， \sqrt{10} x^{2} ， 2 \sqrt{3} x^{2} \cdot \cdot \cdot \cdot \cdot \cdot$ ，第 $n$ 个单项式是（）

A、 $\sqrt{2 n} x^{2}$ B、 $\sqrt{2} n$ C、 $\sqrt{2} n x^{2}$ D、 $(\sqrt{2})^{n} x^{2}$

查看试题解析
9. 已知二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，则点 $(a ， b)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
10. 在多次重复抛掷一枚质地均匀的硬币的试验中，随机事件“正面向上”发生的频率为 $f$ ，每次试验该事件的概率为 $P$ ．下列说法错误的是（）

A、 $P$ 的值为0.5 B、随着试验次数的增加， $f$ 的值可能发生变化 C、当试验次数很大时， $f$ 在 $P$ 附近摆动，并趋于稳定 D、试验次数越多， $f$ 的值越大

查看试题解析
11. 如图， $△ A B C$ 的内切圆 $⊙ O$ 与 $B C$ ， $A C$ ， $A B$ 分别相切于点 $D$ ， $E$ ， $F$ ，且 $∠ C = 90 °$ ， $A C = 8$ ， $B C = 6$ ，则阴影部分（即四边形 $C E O D$ ）的面积为（）

A、4 B、6.25 C、7.5 D、9

查看试题解析
12. 近年来，国内汽车市场经历了翻天覆地的变化，随着新能源的发展普及，越来越多的人购买新能源汽车，燃油汽车销量持续下滑．某款燃油汽车从售价25万元，经过两次降价后售价为16万元．设该款汽车每次降价的平均下降率是 $x$ ，则所列方程正确的是（）

A、 $25 (1 - x)^{2} = 16$ B、 $25 (1 + x)^{2} = 16$ C、 $25 (1 - 2 x) = 16$ D、 $16 (1 + x)^{2} = 25$

查看试题解析

二、填空题（本大题共4小题，每小题2分，满分8分）

13. 红塔区自2018年启动义务教育优质均衡发展创建工作以来，新增义务教育阶段学位5240个，有效应对了首批“全面二孩”入小学高峰期．将数字“5240”用科学记数法表示为．

查看试题解析
14. 若点 $P (1 ， - 17)$ 和点 $Q$ 关于原点对称，则点 $Q$ 的坐标为．

查看试题解析
15. 若方程 $x^{2} + 4 x + 2 = 0$ 的两根为 $m ， n$ ，则 $\frac{1}{m} + \frac{1}{n} =$ ．

查看试题解析
16. 某数学兴趣小组用一张半径为 $30 c m$ 的扇形纸板做成一个圆锥形帽子（接缝忽略不计），如果扇形纸板的面积为 $240 π c m^{2}$ ，那么做成的圆锥形帽子的底面半径为．

查看试题解析

三、解答题（本大题共8小题，满分56分）

17. 解下列方程：

(1)、 $x^{2} + 3 x + 2 = 0$ ；

(2)、 $x^{2} - 2 x - 1 = 0$ ．

查看试题解析
18. 如图， $∠ A B E = ∠ C B D ， A B = E B ， C B = D B$ ．
求证： $A D = E C$ ．

查看试题解析
19. 已知抛物线 $y = x^{2} + b x + c$ 与 $y$ 轴交于点 $(0 ， - 3)$ ，当 $x < 1$ 时， $y$ 随 $x$ 的增大而减小，当 $x > 1$ 时， $y$ 随 $x$ 的增大而增大．

(1)、求 $b ， c$ 的值；

(2)、若点 $P (m ， n)$ （其中 $m \neq 0$ ）在抛物线 $y = x^{2} + b x + c$ 上，求 $\frac{n^{2} + 6 n + 9}{4 m^{4}} + \frac{m - 1}{m^{2}}$ 的值．

查看试题解析
20. 红塔区各义务教育学校按照“一校一案”的要求，每学期坚持以校内教师提供项目为主，按需求从区级“白名单”二次遴选非学科校外培训机构和团体提供相关项目进入学校，拓宽课后服务渠道，满足学生兴趣特长发展需求．甲、乙两名同学准备报名参加学校课后服务活动，各自随机选择篮球、舞蹈、书法三种中的一种，记篮球为 $A$ ，舞蹈为 $B$ ，书法为 $C$ ．假设这两名同学选择参加哪种课后服务活动不受任何因素影响，且每一种被选到的可能性相等．记甲同学的选择为 $x$ ，乙同学的选择为 $y$ ．

(1)、请用列表法或画树状图法中的一种方法，求 $(x ， y)$ 所有可能出现的结果总数；

(2)、求甲、乙两名同学选择参加同一种课后服务活动的概率 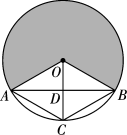$P$ ．

查看试题解析
21. 如图，在 $⊙ O$ 中，弦 $A B$ 和半径 $O C$ 相交于点 $D ， A B$ 与 $O C$ 互相平分，连接 $O A ， O B ， A C ， B C$ ．

(1)、求证：四边形 $O A C B$ 是菱形；

(2)、若扇形 $O B A$ （图中阴影部分）的面积为 $\frac{8}{3} π$ ，求 $O A$ 与 $B C$ 间的距离．

查看试题解析
22. 雪是冬天的来信，碎碎坠琼芳，雪花落处，诗意陡升，在云南，遇见雪山的烂漫，看“高原精灵”翩翩起舞，感受“南国雾凇美如画”的韵味，有一种叫云南的生活，它总是呼唤着你，岁岁年年，四时不变．云南某雪山景区经过市场调查发现，某天门票的销售量 $y$ （单位：张）与门票的售价 $x$ （单位：元/张）的函数关系如图所示，门票售价不低于50元，不高于300元．

(1)、求 $y$ 与 $x$ 的函数解析式（也称关系式）；

(2)、求这一天该景区销售门票获得的总收入 $W$ 的最大值．

查看试题解析
23. 如图， $⊙ O$ 是 $△ A B C$ 的外接圆， $A B$ 是 $⊙ O$ 的直径，点 $D$ 是 $A C$ 延长线上一点，连接 $B D$ ，交 $⊙ O$ 于点 $E$ ，点 $F$ 在 $B D$ 上， $∠ D C F = ∠ A B C$ ．

(1)、试判断直线 $C F$ 与 $⊙ O$ 的位置关系，并证明你的结论；

(2)、若 $\overset{⌢}{B E} = \overset{⌢}{C E} ， \frac{A C}{B C} = \frac{3}{4} ， B D = \sqrt{5}$ ，求 $⊙ O$ 的半径．

查看试题解析
24. 我国著名数学家华罗庚曾说过：“数与形，本是相倚依，焉能分作两边飞．数缺形时少直观，形少数时难入微；数形结合百般好，割裂分家万事非．切莫忘，几何代数统一体，永远联系，切莫分离！”数形结合是解决数学问题的重要思想方法．请结合所学的数学解决下列问题．
在平面直角坐标系中，若点的横坐标、纵坐标都为整数，则称这样的点为整点．
设函数 $y = (k + 2) x^{2} - (3 k - 2) x + 2 k - 4$ （实数 $k$ 为常数）的图象为图象 $T$ ．

(1)、求证：无论 $k$ 取什么实数，图象 $T$ 与 $x$ 轴总有公共点；

(2)、是否存在非负整数 $k$ ，使图象 $T$ 与 $x$ 轴的公共点都是整点？若存在，求所有非负整数 $k$ 的值；若不存在，请说明理由．

查看试题解析