四川省成都市简阳市2023-2024学年七年级上学期期末数学试题
试卷更新日期:2024-04-16 类型:期末考试
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上)
-
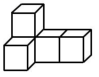
1. -3的相反数是( )A、 B、-3 C、3 D、2. 如图,是由几个相同的小正方体堆砌成的几何体,从左面看到该几何体的形状图是( )
 A、
A、 B、
B、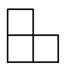 C、
C、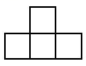 D、
D、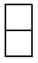 3. 以凤凰和梧桐为主要意象的简阳文体中心如腾飞之仪凤,彰显了千年文脉的传承。其体育馆内部建筑面积约为2.8万平方米,将2.8万用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 下列调查方式中,不适合的是( )A、了解沱江的水质,采用抽样调查方式 B、为了准确了解全国人口状况,采用普查方式 C、了解某市中小学生睡眠时间,采用抽样调查方式 D、了解中央电视台春节联欢晚会的收视率,采用普查方式6. 若与是同类项,则有( )A、m=1,n=2 B、m=1,n=-1 C、m=0,n=-1 D、m=0,n=27. 如图,点A、B、C不在一条直线上,先作直线BC , 再过点A作射线AD与线段BC交于点D , 下列正确的作图是( )
3. 以凤凰和梧桐为主要意象的简阳文体中心如腾飞之仪凤,彰显了千年文脉的传承。其体育馆内部建筑面积约为2.8万平方米,将2.8万用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 下列调查方式中,不适合的是( )A、了解沱江的水质,采用抽样调查方式 B、为了准确了解全国人口状况,采用普查方式 C、了解某市中小学生睡眠时间,采用抽样调查方式 D、了解中央电视台春节联欢晚会的收视率,采用普查方式6. 若与是同类项,则有( )A、m=1,n=2 B、m=1,n=-1 C、m=0,n=-1 D、m=0,n=27. 如图,点A、B、C不在一条直线上,先作直线BC , 再过点A作射线AD与线段BC交于点D , 下列正确的作图是( ) A、
A、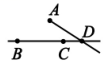 B、
B、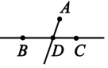 C、
C、 D、
D、 8. 我国古代《孙子算经》中记载了“多人共车”问题:今有三人共车,二车空,二人共车,九人步,问人与车各几何?其大意是:若3个人乘一辆车,则空2辆车;若2个人乘一辆车,则有9个人要步行,问人与车各是多少?若设有x辆车,则可列方程是( )A、 B、 C、 D、
8. 我国古代《孙子算经》中记载了“多人共车”问题:今有三人共车,二车空,二人共车,九人步,问人与车各几何?其大意是:若3个人乘一辆车,则空2辆车;若2个人乘一辆车,则有9个人要步行,问人与车各是多少?若设有x辆车,则可列方程是( )A、 B、 C、 D、二、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)
-
9. 上午10:00时,钟表上时针和分针的夹角为度.10. 在四个有理数1.5, , 0,中,最小的数是 .11. 已知是方程的解,则 .12. 请写出一个系数是-5的三次单项式 .13. 将字母“O”,“S”按照如图所示的规律摆放,依次下去,则第6个图形中字母“O”的个数是 .

三、解答题(本大题共5个小题,共48分,解答过程写在答题卡上)
-
14. 计算:(1)、;(2)、 .15. 解方程:(1)、;(2)、 .16. 先化简,再求值: , 其中 , .17. 《水浒传》、《三国演义》、《西游记》、《红楼梦》被称为中国四大名著,某中学的兴趣小组想了解全校学生对四大名著的喜爱情况,随机抽取了部分学生进行调查统计,要求每名学生从中选出一本自己最喜爱的名著,并将调查结果绘制成如下统计图(其中《水浒传》、《三国演义》、《西游记》、《红楼梦》分别用A、B、C、D表示),请你结合图中信息解答下列问题:
 (1)、本次调查的学生人数是人;(2)、请把条形统计图补充完整;(3)、在扇形统计图中,B对应的圆心角的度数是;(4)、已知该中学共有3000名学生,请根据样本估计全校最喜爱《西游记》的人数是多少?18. 如图,点O是数轴的原点,点A在数轴上位于原点左侧,点B在数轴上位于原点右侧, .
(1)、本次调查的学生人数是人;(2)、请把条形统计图补充完整;(3)、在扇形统计图中,B对应的圆心角的度数是;(4)、已知该中学共有3000名学生,请根据样本估计全校最喜爱《西游记》的人数是多少?18. 如图,点O是数轴的原点,点A在数轴上位于原点左侧,点B在数轴上位于原点右侧, . (1)、当 , 时,点A表示的数为 , 点B表示的数为;(2)、若点C、D为数轴上任意两点,点M是线段AC的中点,点N是线段BD的中点.
(1)、当 , 时,点A表示的数为 , 点B表示的数为;(2)、若点C、D为数轴上任意两点,点M是线段AC的中点,点N是线段BD的中点.①当点C与点D重合时,探究AB与MN的数量关系,并说明理由.
②当时,直接写出MN的长度(用m , n表示).
四、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)
-
19. 若 , 则 .20. 若a , b互为相反数,a+1的倒数是 , 则b的值为 .21. a , b在数轴上表示的数如图所示,则有b(填“>”或“<”).
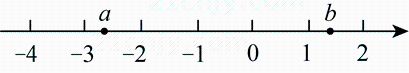 22. 已知线段 , 点C是直线AB上一点,点D为线段AC的中点, , 且m、n满足 , 则线段BD的长为 .23. 如图,等边△ABC的边长为4cm,P、Q两点分别从A、B两点同时出发﹐点P以8cm/s的速度按顺时针方向在等边△ABC的边上运动,点Q以2cm/s的速度按逆时针方向在等边△ABC的边上运动,则P、Q两点第一次在等边△ABC顶点处相遇的时间秒,第四次在等边△ABC顶点处相遇的时间秒.
22. 已知线段 , 点C是直线AB上一点,点D为线段AC的中点, , 且m、n满足 , 则线段BD的长为 .23. 如图,等边△ABC的边长为4cm,P、Q两点分别从A、B两点同时出发﹐点P以8cm/s的速度按顺时针方向在等边△ABC的边上运动,点Q以2cm/s的速度按逆时针方向在等边△ABC的边上运动,则P、Q两点第一次在等边△ABC顶点处相遇的时间秒,第四次在等边△ABC顶点处相遇的时间秒.
五、解答题(本大题共3个小题,共30分,解答过程写在答题卡上)
-
24. 第31届世界大学生夏季运动会在成都举办,吉祥物“蓉宝”深受大家的喜爱.某商场从厂家购进了成都大运会吉祥物蓉宝毛绒公仔和3D钥匙扣两种商品,每个毛绒公仔的进价比每个3D钥匙扣的进价多30元.若购进毛绒公仔4个,3D钥匙扣5个,共需要570元.(1)、求毛绒公仔、3D钥匙扣两种商品的每个进价分别是多少元?(2)、该商场从厂家购进成都大运会吉祥物蓉宝毛绒公仔和3D钥匙扣两种商品共60个,所用资金恰好为4200元.在销售时,每个毛绒公仔的售价为100元,要使得这60个商品卖出后获利25%,则每个3D钥匙扣的售价应定为多少元?25. 【阅读理解】
在计算机上可以设置程序,将二次多项式处理成一次多项式,设置程序为:将二次多项式A的二次项系数乘以2作为一次多项式B的一次项系数,将二次多项式A的一次项系数作为一次多项式B的常数项.
例如: , A经过程序设置得到 .
【知识应用】
关于x的二次多项式A经过程序设置得到一次多项式B , 已知 , 根据上方阅读材料,解决下列问题:
(1)、若 , 求m , n的值;(2)、若的结果中不含一次项,求关于x的方程的解;(3)、某同学在计算时,把A-2B看成了 , 得到的结果是 , 求出的正确值.26. 如图,点O在直线AB上,射线OC , OE在与OA重合的位置同时开始绕点O顺时针旋转,OC的旋转速度为每秒2°,OE的旋转速度为每秒6°,当OE与OB重合时停止旋转,在OC的右侧作射线OD使得 , 设旋转时间为t秒.解答下列问题: (1)、当秒时,则 , ;(2)、当的平分线OM与射线OE所组成的时,求旋转时间t ,(3)、是否存在一个常数m , 使得的值在一定时间范围内不随t的改变而改变?若存在,求出m的值;若不存在,请说明理由.
(1)、当秒时,则 , ;(2)、当的平分线OM与射线OE所组成的时,求旋转时间t ,(3)、是否存在一个常数m , 使得的值在一定时间范围内不随t的改变而改变?若存在,求出m的值;若不存在,请说明理由.