四川省成都市新都区2023-2024学年八年级上学期期末考试数学试题

试卷更新日期：2024-04-16 类型：期末考试

进入出卷网下载

一、选择题(本大题共8个小题，每小题4分，共32分；在每个小题给出的四个选项中，有且只有一个答案是符合题目要求的，并将自己所选答案的字母涂在答题卡上

1. 平面直角坐标系中，在第一象限的点为（）

A、 $(1 ， 3)$ B、 $(- 1 ， 3)$ C、 $(- 1 ， - 3)$ D、 $(1 ， - 3)$

查看试题解析
2. 下列各数为无理数的是（）

A、 $\frac{2}{5}$ B、 $π$ C、 $1 . \dot{2}$ D、 $3.1415926$

查看试题解析
3. 下列命题为真命题的是（）

A、同旁内角互补 B、若 $a^{2} = b^{2}$ ，则 $a = b$ C、在同一平面内，垂直同一条直线的两条直线互相平行 D、如果一个整数能被3整除，那么这个数也能被6整除

查看试题解析
4. 下列给出的四组数中，不能构成直角三角形三边的一组是（）

A、 $1 ， 2 ， \sqrt{5}$ B、 $2 ， 3 ， 4$ C、 $3 ， 4 ， 5$ D、 $5 ， 12 ， 13$

查看试题解析
5. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{16}$ C、 $\sqrt{3}$ D、 $\sqrt{48}$

查看试题解析
6. 关于函数 $y = 3 x + 1$ ，下列结论正确的是（）

A、函数图象过一、二、三象限 B、函数图象是一条线段 C、 $y$ 随 $x$ 增大而减小 D、点 $(1 ， 3)$ 在函数图象上

查看试题解析
7. $1992$ 年巴塞罗那奥运会混合双向飞碟金牌获得者—“神枪手”张山于 $2023$ 年 $11$ 月走进新都某中学，现场分享励志经历，在某次训练中，张山的成绩如下： $197 ， 196 ， 194 ， 196 ， 196 ， 199$ (单位：个)，这些成绩的中位数和众数分别是（）

A、 $196 ， 195$ B、 $195 ， 196$ C、 $196 ， 199$ D、 $196 ， 196$

查看试题解析
8. 2023年成都大运会上，努力拼搏的不只有运动员们，在赛场外，到处都能看到志者们忙碌的身影，大批大学生报名参与志愿者服务工作，某大学计划组织本校学生志愿者乘车去了解比赛场馆情况，若单独调配30座(不含司机)客车若干辆，则有5人没有座位；若只调配25座(不含司机)客车，则用车数量将增加3辆，并空出5个座位．设计划调配30座客车 $x$ 辆，该大学共有 $y$ 名大学生志愿者，则下列方程组正确的是（）

A、 ${\begin{array}{l} 30 x = y + 5 \\ 25 (x + 3) = y - 5 \end{array}$ B、 ${\begin{array}{l} 30 x = y - 5 \\ 25 (x + 3) = y + 5 \end{array}$ C、 ${\begin{array}{l} 30 x = y \\ 25 (x + 3) = y + 5 \end{array}$ D、 ${\begin{array}{l} 30 x = y - 5 \\ 25 (x + 3) = y - 5 \end{array}$

查看试题解析

二、填空题(本大题共5个小题，每小题4分，共20分，答案写在答题卡上

9. $- 8$ 的立方根是．

查看试题解析
10. 在平面直角坐标系中，点P（3，5）关于x轴对称的点的坐标是．

查看试题解析
11. 若式子 $\sqrt{x - 2}$ 有意义，则x的取值范围是.

查看试题解析
12. 如图，在 $△ A B C$ 中， $∠ A = 6 0^{∘}$ ， $∠ 1 = 2 0^{∘}$ ， $∠ 2 = 3 0^{∘}$ ，则 $∠ B D C$ 的度数是

查看试题解析
13. 如图，在长方形纸片 $A B C D$ 中， $A B = 3$ ， $A D = 5$ ，如图所示折叠纸片，使点 $A$ 落在 $B C$ 边上的 $A^{'}$ 处，折痕为 $P D$ ，此时 $B P$ 的长为

查看试题解析

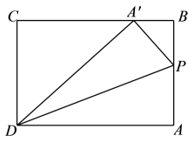
三、解答题(本大题共5小题，共48分，解答过程写在答题卡上

14. 计算：

(1)、 $| - 3 | - {(\sqrt{2})}^{2} + {(4 - \sqrt{3})}^{0} + 2^{- 1} \times 8$

(2)、 ${\begin{array}{l} 3 x - 4 (x - 2 y) = 5 \\ x - 2 y = 1 \end{array}$

查看试题解析
15. 如图，在平面直角坐标系中， $△ A B C$ 的顶点 $A (- 1 ， 3)$ ， $B (3 ， 1)$ ， $C (4 ， 4)$ 均在正方形网格的格点上

(1)、画出 $△ A B C$ 关于 $x$ 轴对称的图形 $△ A^{'} B^{'} C^{'}$ ，并写出顶点 $B^{'}$ 的坐标；

(2)、在 $y$ 轴上求作一点 $P$ ，使 $P C + P B$ 的值最小，并求出最小值．

查看试题解析
16. 杨升庵，四川新都人，明代文学家、学者、官员，他的著作数量之繁多，范围之广博，内容之丰富，在整个中国文化史上都鲜有人比肩，堪称是一位百科全书式的学者.某校开展了“弘扬升庵精神，学习传统文化”读书活动，为了解学生课外阅读中国古代文学作品情况，随机调查了 $50$ 名同学平均每周课外阅读用时，如图是根据调查所得的数据绘制的统计图的一部分，请根据以上信息，解答下列问题

(1)、补全条形统计图；

(2)、在这次调查的数据中，平均每周课外阅读所用时间的众数是小时，中位数是小时；

(3)、若该校共有 $1600$ 名学生，根据以上调查结果估计该校全体学生平均每周课外古诗词阅读用时不低于 $3$ 小时的同学共有多少人?

查看试题解析
17. 如图，已知 $C F ⊥ A E$ ， $A B ⊥ A E$ ， $∠ A B C + ∠ D F C = 180 °$

(1)、求证∶ $D F ∥ B C$ ；

(2)、若 $C F$ 平分 $∠ B C E$ ， $E F = C D = 3$ ，求 $C F$ 的长度

查看试题解析
18. 如图，直线 $y = k x + 3$ 经过点 $B (- 1 ， 4)$ 和点 $A (5 ， m)$ ，与x轴交于点C

(1)、求k ， m的值；

(2)、求 $△ A O B$ 的面积；

(3)、若点P在x轴上，当 $△ P B C$ 为等腰三角形时，直接写出此时点P的坐标

查看试题解析

四、填空题(本大题共5个小题，每小题4分，共20分，答案写在答题卡上

19. 比较大小： $\frac{\sqrt{5} - 1}{2}$ $\frac{3}{4}$ （填“＞”、“＜”或“=”）

查看试题解析
20. 若关于 $x$ 、 $y$ 的方程组 ${\begin{array}{l} x + 2 y = 3 m - 1 \\ x + y = 5 \end{array}$ 的解满足 $2 x + 3 y = 19$ ，则 $m$ 的值为．

查看试题解析
21. 若一组数据 $x_{1} ， x_{2} ， ⋯ ， x_{n}$ 的平均数为17，方差为3，则另一组数据 $2 x_{1} + 2$ ， $2 x_{2} + 2$ ， $⋯ 2 x_{n} + 2$ 的平均数是，方差是

查看试题解析
22. 如图 $1$ ，在平面直角坐标系中，等腰 $△ A B C$ 在第一象限，且 $A C ∥ x$ 轴，直线 $y = x$ 从原点 $O$ 出发沿 $x$ 轴正方向平移，在平移过程中，直线被 $△ A B C$ 截得的线段长度 $n$ 与直线在 $x$ 轴上平移的距离 $m$ 的函数图象如图 $2$ 所示，那么 $△ A B C$ 的面积为

查看试题解析
23. 如图，在平面直角坐标系中， $△ A B C$ 的顶点坐标分别为 $A (- 4 ， 1)$ ， $B (0 ， 5)$ ， $C (0 ， 1)$ ，点 $D$ 与点 $A$ 关于 $y$ 轴对称，连接 $B D$ ，在边 $A B$ 上取一点 $E$ ，在 $B D$ 的延长线上取一点 $F$ ，并且满足 $A E = D F$ ，连接 $E F$ 交边 $A D$ 于点 $G$ ，过点 $G$ 作 $E F$ 的垂线交 $y$ 轴于点 $H$ ，则点 $H$ 的坐标为

查看试题解析

五、解答题(本大题共3个小题，共30分，解答过程写在答题卡上

24. “低碳生活，绿色出行”理念的普及，新能源汽车正逐渐成为人们喜爱的交通工具，某汽车销售公司计划购进一批新能源汽车尝试进行销售；据了解， $2$ 辆 $A$ 型汽车、 $3$ 辆 $B$ 型汽车的进价共计 $80$ 万元； $3$ 辆 $A$ 型汽车、 $2$ 辆 $B$ 型汽车的进价共计 $95$ 万元

(1)、求 $A$ ， $B$ 两种型号的汽车每辆进价分别为多少万元?

(2)、若该公司计划购进以上两种型号的新能源汽车(两种型号的汽车均购买)共 $20$ 辆，且 $A$ (型汽车不超过 $6$ 辆，根据市场调查，销售 $1$ 辆 $A$ 型汽车可获利 $0.8$ 万元，销售 $1$ 辆 $B$ 型汽车可获利 $0.5$ 万元，请问怎么安排采购方案获利最大?

查看试题解析
25. 如图，在平面直角坐标系中，直线 $l$ 与 $x$ 轴交于点 $A (- 4 ， 0)$ ，与 $y$ 轴交于点 $B (0 ， 2)$ ，已如点 $C (- 2 ， 0)$ .

(1)、求直线 $l$ 的表达式；

(2)、点 $P$ 是直线 $l$ 上一动点，且 $△ B O P$ 和 $△ C O P$ 的面积相等，求点 $P$ 坐标；

(3)、在平面内是否存在点 $Q$ ，使得 $△ A B Q$ 是以 $A B$ 为底的等腰直角三角形?若存在，请求出所有符合条件的点 $Q$ 的坐标；若不存在，请说明理由.

查看试题解析
26. 在 $△ A B C$ 中， $A B = B C ， ∠ A B C = 9 0^{∘}$ ，点 $D$ 是边 $A C$ 上一点，连接 $D B$ ，过点 $C$ 作直线 $B D$ 的垂线，垂足为点 $E$

(1)、如图1，若 $A F ⊥ B D$ 于点 $F$ ，求证： $C E = B F$ ；

(2)、如图2，在线段 $E C$ 上截取 $E G = E B$ ，连接 $A G$ 交 $B D$ 于点 $H$ ，求证： $C G = 2 E H$ ；

(3)、如图3，若点 $D$ 为 $A C$ 的中点，点 $M$ 是线段 $B C$ 延长线上的一点，连接 $D M$ ，求 $C M$ ， $B M$ ， $D M$ 的数量关系

查看试题解析