四川省宜宾市叙州区2023-2024学年七年级上学期期末数学试题
试卷更新日期:2024-04-16 类型:期末考试
一、选择题(本大题共12个小题,每小题4分,共48分).在每小题给出的四个选项中,只有一项是符合题目要求的.(注意:在试题卷上作答无效)
-
1. 2024的绝对值是( )A、2024 B、 C、 D、2. 下列各数中最大的数是( )A、 B、1 C、0 D、3. 已建成的宜宾站是宜宾最大的高铁站,是现有宜宾西站面积的4倍,其建筑规模达158000平方米,将158000用科学记数法表示为( )A、 B、 C、 D、4. 如图,由4个相同的小立方块搭成的几何体,这个几何体的俯视图是( )
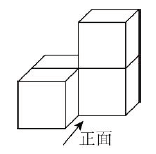 A、
A、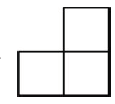 B、
B、 C、
C、 D、
D、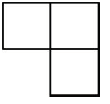 5. 下列判断正确的是( )A、的系数是2 B、与是同类项 C、单项式的次数是7 D、是二次三项式6. 已知 , 则代数式的值为( )A、3 B、 C、1 D、7. 下列式子变形正确的是( )A、 B、 C、 D、8. 如图,将一块直角三角板的直角顶点放在直尺的一边上,当时,则( )
5. 下列判断正确的是( )A、的系数是2 B、与是同类项 C、单项式的次数是7 D、是二次三项式6. 已知 , 则代数式的值为( )A、3 B、 C、1 D、7. 下列式子变形正确的是( )A、 B、 C、 D、8. 如图,将一块直角三角板的直角顶点放在直尺的一边上,当时,则( )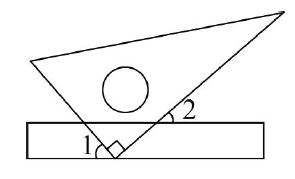 A、41° B、49° C、59° D、31°9. 若 , 则等于( )A、 B、 C、1 D、202410. 如图,是一个正方体的展开图,若相对面上的两个数互为相反数,则代数式的值是( )
A、41° B、49° C、59° D、31°9. 若 , 则等于( )A、 B、 C、1 D、202410. 如图,是一个正方体的展开图,若相对面上的两个数互为相反数,则代数式的值是( )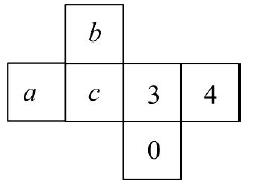 A、6 B、 C、18 D、11. 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳记数”.一位书生坚持每天五更起床读书,为了勉励自己,他用“结绳记数”的方法来记录自己读书的天数,如图1是他从右到左依次排列的绳子上打结,满七进一,表示的天数为66天.按同样的方法,图2表示的天数是( )
A、6 B、 C、18 D、11. 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳记数”.一位书生坚持每天五更起床读书,为了勉励自己,他用“结绳记数”的方法来记录自己读书的天数,如图1是他从右到左依次排列的绳子上打结,满七进一,表示的天数为66天.按同样的方法,图2表示的天数是( ) A、72 B、343 C、366 D、103212. 如图,是的角平分线, , 是的角平分线,有下列四个结论:①;②;③;④ . 其中,正确的个数为( )
A、72 B、343 C、366 D、103212. 如图,是的角平分线, , 是的角平分线,有下列四个结论:①;②;③;④ . 其中,正确的个数为( )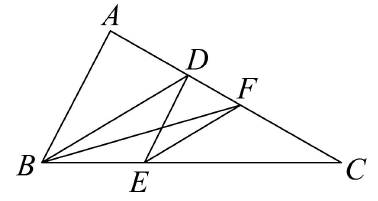 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(本大题共6个小题,每小题4分,共24分).请把答案直接填在答题卡对应题目中的横线上.(注意:在试题卷上作答无效)
-
13. 智轨已成为宜宾人生活中非常重要的交通工具.若智轨向东行驶记为正,则向西行驶记作 .14. 将多项式按字母x降幂排列为 .15. 如图,已知线段 , , 点D是线段的中点,则线段 .
 16. 已知有理数a、b、c在数轴上的位置如图所示,化简: .
16. 已知有理数a、b、c在数轴上的位置如图所示,化简: . 17. 如图,已知直线 , 点M , N分别在直线 , 上,点E为 , 之间一点,且点E在线段的右侧, . 若与的平分线相交于点 , 与的平分线相交于点 , 与的平分线相交于点 , ……以此类推,若 , 则n的值是 .
17. 如图,已知直线 , 点M , N分别在直线 , 上,点E为 , 之间一点,且点E在线段的右侧, . 若与的平分线相交于点 , 与的平分线相交于点 , 与的平分线相交于点 , ……以此类推,若 , 则n的值是 . 18. 如图,直角三角形中, , , , , 点D是边上一动点,作直线经过点C、点D , 分别过点A , B作与垂直,与垂直,垂足分别为点F , E . 设线段 , 的长度分别为 , , 则的最大值为 .
18. 如图,直角三角形中, , , , , 点D是边上一动点,作直线经过点C、点D , 分别过点A , B作与垂直,与垂直,垂足分别为点F , E . 设线段 , 的长度分别为 , , 则的最大值为 .
三、解答题:(本大题共7个小题,共78分)解答题应写出必要的文字说明,证明过程或演算步骤.(注意:在试题卷上作答无效)
-
19. 计算:(1)、(2)、20. 先化简再求值: , 其中 , .21. 完成下面的证明.如图,已知平分 , , 求证: .

证明:(已知)
▲ ( ▲ )
▲ ( ▲ )
平分(已知)
▲ (角平分线的定义)
( ▲ ).
22. 已知代数式 , .(1)、当 , 时,求的值;(2)、若的值与y的取值无关,求x的值.23. 如图,点O是直线上一点,以O为顶点作 , 平分 . (1)、当时,求的度数;(2)、若与互补,求的度数.24. 绿源超市销售茶壶、茶杯,茶壶每只定价50元,茶杯每只定价6元.春节期间,超市将开展促销活动,向顾客提供两种优惠方案:
(1)、当时,求的度数;(2)、若与互补,求的度数.24. 绿源超市销售茶壶、茶杯,茶壶每只定价50元,茶杯每只定价6元.春节期间,超市将开展促销活动,向顾客提供两种优惠方案:方案一:每买一只茶壶就赠一只茶杯;
方案二:茶壶和茶杯都按定价的90%付款.
某顾客计划到该超市购买茶壶8只和茶杯x只(茶杯数多于8只).
(1)、用含x的代数式分别表示方案一与方案二各需付款多少元?(2)、当时,请通过计算说明该顾客选择上面的两种购买方案哪种更省钱?25. 已知直线 , 点E和点F分别在直线和上. (1)、如图1,射线平分交于点G , 若 , 求的度数;(2)、如图2,射线平分 , 点M是射线上一点(不包括端点F),点N为的平分线上一点(不包括端点E),连结 , , 延长交射线于点H , 猜想与的关系,并说明理由;(3)、在(1)的条件下,若绕点G以每秒转动的速度逆时针旋转一周,同时绕点F以每秒转动的速度逆时针旋转,设转动时间为t秒,当转动结束时也随即停止转动,在整个转动过程中,当和互相平行时,请直接写出此时t的值.
(1)、如图1,射线平分交于点G , 若 , 求的度数;(2)、如图2,射线平分 , 点M是射线上一点(不包括端点F),点N为的平分线上一点(不包括端点E),连结 , , 延长交射线于点H , 猜想与的关系,并说明理由;(3)、在(1)的条件下,若绕点G以每秒转动的速度逆时针旋转一周,同时绕点F以每秒转动的速度逆时针旋转,设转动时间为t秒,当转动结束时也随即停止转动,在整个转动过程中,当和互相平行时,请直接写出此时t的值.