四川省广元市剑阁县2023-2024学年九年级上学期期末数学试题
试卷更新日期:2024-04-16 类型:期末考试
一、选择题:本题共10小题,每小题3分,共30分。每小题给出的四个选项中,只有一个符合题意,请将符合题意的选项的字母填写在答题卡上。
-
1. 在下面用数学家名字命名的图形中,既是轴对称图形又是中心对称图形的是( )
 A、斐波那契螺旋线 B、笛卡尔心形线 C、赵爽弦图 D、科克曲线2. 关于一元二次方程根的情况,下列说法中正确的是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法确定3. 下列事件中,是随机事件的是( )A、三角形中任意两边之和大于第三边 B、太阳从东方升起 C、车辆随机到达一个路口,遇到绿灯 D、一个有理数的绝对值为负数4.
A、斐波那契螺旋线 B、笛卡尔心形线 C、赵爽弦图 D、科克曲线2. 关于一元二次方程根的情况,下列说法中正确的是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法确定3. 下列事件中,是随机事件的是( )A、三角形中任意两边之和大于第三边 B、太阳从东方升起 C、车辆随机到达一个路口,遇到绿灯 D、一个有理数的绝对值为负数4.如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=65°,∠E=70°,且AD⊥BC,则∠BAC的度数为( )
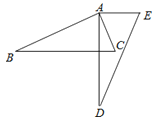 A、60° B、85° C、75° D、90°5. 关于抛物线 , 下列说法不正确的是( )A、图像开口向下 B、顶点坐标是 C、对称轴是直线 D、当时,随的增大而增大6. 如图,分别切于点 , 点是上一点,且 , 则( )
A、60° B、85° C、75° D、90°5. 关于抛物线 , 下列说法不正确的是( )A、图像开口向下 B、顶点坐标是 C、对称轴是直线 D、当时,随的增大而增大6. 如图,分别切于点 , 点是上一点,且 , 则( ) A、 B、 C、 D、7. 近年来,由于新能源汽车的崛起,燃油汽车的销量出现了不同程度的下滑,经销商纷纷开展降价促销活动.某款燃油汽车今年2月份售价为23万元,4月份售价为18.63万元,设该款汽车这两月售价的月平均降价率是 , 则所列方程正确的是( )A、 B、 C、 D、8. 如图,以为顶点的二次函数的图象与轴负半轴交于点,则一元二次方程的正数解的范围是( )
A、 B、 C、 D、7. 近年来,由于新能源汽车的崛起,燃油汽车的销量出现了不同程度的下滑,经销商纷纷开展降价促销活动.某款燃油汽车今年2月份售价为23万元,4月份售价为18.63万元,设该款汽车这两月售价的月平均降价率是 , 则所列方程正确的是( )A、 B、 C、 D、8. 如图,以为顶点的二次函数的图象与轴负半轴交于点,则一元二次方程的正数解的范围是( ) A、 B、 C、 D、9. 如图,与正六边形的边分别交于点 , 点为劣弧的中点.若 , 则的半径为( )
A、 B、 C、 D、9. 如图,与正六边形的边分别交于点 , 点为劣弧的中点.若 , 则的半径为( ) A、2 B、 C、 D、10. 已知二次函数 , 当时,的最小值为-4,则的值为( )A、或4 B、或 C、或4 D、或4
A、2 B、 C、 D、10. 已知二次函数 , 当时,的最小值为-4,则的值为( )A、或4 B、或 C、或4 D、或4二、填空题:本题共6小题,每小题4分,共24分。把正确答案直接填写在答题卡相应的位置上。
-
11. 若把二次函数化为的形式,其中为常数,则 .12. 在如图所示的电路图中,当随机闭合开关中的任意一个时,能够使小灯泡发光的概率为 .
 13. 已知点P为平面内一点,若点P 到⊙O上的点的最长距离为5,最短距离为1,则⊙O 的半径为 .
13. 已知点P为平面内一点,若点P 到⊙O上的点的最长距离为5,最短距离为1,则⊙O 的半径为 .
14. 一个不透明的箱子里装有个球,其中红球4个,这些球除颜色不同其余都相同,每次搅拌均匀后,任意摸出一个球记下颜色后再放回,大量重复试验发现,摸到红球的频率稳定在0.25附近,则可以估算出的值为 .15. 如图,在中, , 以为直径作半圆,交于点 , 交于点 , 则弧的长为(结果保留)。 16. 在如图所示的平面直角坐标系中,是边长为2的等边三角形,作与关于点成中心对称,再作与关于点成中心对称,…,如此作下去,则的顶点的坐标是 .
16. 在如图所示的平面直角坐标系中,是边长为2的等边三角形,作与关于点成中心对称,再作与关于点成中心对称,…,如此作下去,则的顶点的坐标是 .
三、解答题:(本大题共10个小题,共96分。解答时应写出必要的文字说明、证明过程或演算步骤。)
-
17. 解方程:(1)、(2)、18. 如图,在中,是直径,且交圆于 , 求证: .
 19. 已知关于的一元二次方程(1)、求证:方程有两个不相等的实数根。(2)、已知该方程的两个根为 , 且满足 , 求的值.20. 如图,在边长为1个单位长度的小正方形组成的网格中,与关于点成中心对称,与的顶点均在格点上,请按要求完成下列各题.
19. 已知关于的一元二次方程(1)、求证:方程有两个不相等的实数根。(2)、已知该方程的两个根为 , 且满足 , 求的值.20. 如图,在边长为1个单位长度的小正方形组成的网格中,与关于点成中心对称,与的顶点均在格点上,请按要求完成下列各题. (1)、在图中画出点的位置;(2)、将绕点顺时针旋转后得到 , 求线段在旋转过程中扫过的面积(结果保留)21. 如图,AB为⊙O的直径,CD是弦,且AB⊥CD于点E . 连接AC、OC、BC.
(1)、在图中画出点的位置;(2)、将绕点顺时针旋转后得到 , 求线段在旋转过程中扫过的面积(结果保留)21. 如图,AB为⊙O的直径,CD是弦,且AB⊥CD于点E . 连接AC、OC、BC. (1)、试说明:;(2)、若 , 求弦的长.22. 目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利.某校九年级某数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了人(每名学生必选一种且只能从这四种中选择一种),并将调查结果绘制成如下不完整的统计图.
(1)、试说明:;(2)、若 , 求弦的长.22. 目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利.某校九年级某数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了人(每名学生必选一种且只能从这四种中选择一种),并将调查结果绘制成如下不完整的统计图. (1)、根据图中信息求出 , ;(2)、请你帮助他们将这两个统计图补全;(3)、已知A , B两位同学都最认可“微信”,C同学最认可“支付宝”,D同学最认可“网购”,从这四名同学中抽取两名同学,请你通过树状图或表格,求出这两名同学最认可的新生事物不一样的概率.23. 为充分利用现有资源,某校“牧春园”计划用一块矩形地种植两种花卉.如图,矩形地一面靠墙(墙的长度为),另外三面用栅栏围成,中间再用栅栏把它分成两个面积相等的矩形.已知栅栏的总长度为 .
(1)、根据图中信息求出 , ;(2)、请你帮助他们将这两个统计图补全;(3)、已知A , B两位同学都最认可“微信”,C同学最认可“支付宝”,D同学最认可“网购”,从这四名同学中抽取两名同学,请你通过树状图或表格,求出这两名同学最认可的新生事物不一样的概率.23. 为充分利用现有资源,某校“牧春园”计划用一块矩形地种植两种花卉.如图,矩形地一面靠墙(墙的长度为),另外三面用栅栏围成,中间再用栅栏把它分成两个面积相等的矩形.已知栅栏的总长度为 . (1)、若矩形地的面积为 , 求的长;(2)、当边为多少时,矩形地的面积最大,最大面积是多少?24. 如图,以四边形的对角线为直径作圆,圆心为 , 过点作的延长线于点 , 已知平分 .
(1)、若矩形地的面积为 , 求的长;(2)、当边为多少时,矩形地的面积最大,最大面积是多少?24. 如图,以四边形的对角线为直径作圆,圆心为 , 过点作的延长线于点 , 已知平分 . (1)、求证:是切线;(2)、若 , 求的半径和的长.25. 在中, , 点为边上任意一点(与不重合),以为直角边构造等腰直角三角形为的中点.
(1)、求证:是切线;(2)、若 , 求的半径和的长.25. 在中, , 点为边上任意一点(与不重合),以为直角边构造等腰直角三角形为的中点. (1)、如图2,将绕点旋转,当点与重合时,求证:;(2)、如图3,将绕点旋转,当点在上且时,求证: .26. 如图,在平面直角坐标系中,二次函数的图象与轴交于两点,与轴交于点 , 点A在原点的左侧,点的坐标为 , 点是抛物线上一个动点,且在直线的上方.
(1)、如图2,将绕点旋转,当点与重合时,求证:;(2)、如图3,将绕点旋转,当点在上且时,求证: .26. 如图,在平面直角坐标系中,二次函数的图象与轴交于两点,与轴交于点 , 点A在原点的左侧,点的坐标为 , 点是抛物线上一个动点,且在直线的上方. (1)、求这个二次函数的解析式;(2)、当点运动到什么位置时,的面积最大?请求出点的坐标和面积的最大值.(3)、连接 , 并把沿翻折,得到四边形 , 那么是否存在点 , 使四边形为菱形?若存在,请求出此时点的坐标;若不存在,请说明理由.
(1)、求这个二次函数的解析式;(2)、当点运动到什么位置时,的面积最大?请求出点的坐标和面积的最大值.(3)、连接 , 并把沿翻折,得到四边形 , 那么是否存在点 , 使四边形为菱形?若存在,请求出此时点的坐标;若不存在,请说明理由.