四川省广安市邻水县2023-2024学年九年级上学期数学期末考试试卷

试卷更新日期：2024-04-16 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分．每小题只有一个选项符合题意，请将所选选项填涂在答题卡上）

1. 下列图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，点A ， B ， C均在 $⊙ O$ 上，若 $∠ B O C = 46 °$ ，则 $∠ B A C =$ （）

A、 $42 °$ B、 $25 °$ C、 $23 °$ D、 $20 °$

查看试题解析
3. 把抛物线 $y = 5 x^{2}$ 向下平移2个单位长度后，与y轴的交点的坐标为（）

A、 $(0 ， - 2)$ B、 $(- 2 ， 0)$ C、 $(2 ， 0)$ D、 $(0 ， 2)$

查看试题解析
4. 下列成语所描述的事件属于不可能事件的是（）

A、水落石出 B、水涨船高 C、水滴石穿 D、水中捞月

查看试题解析
5. 关于x的一元二次方程 $x^{2} - 3 x + 2 - m^{2} = 0$ 的根的情况（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定

查看试题解析
6. 如图，将 $R t △ A B C$ 绕点 $A$ 顺时针方向旋转到 $△ A B_{1} C_{1}$ 的位置，使得点 $C ， A$ ， $B_{1}$ 在同一条直线上， $∠ B = 25 °$ ，那么旋转角等于（）

A、 $65 °$ B、 $100 °$ C、 $115 °$ D、 $120 °$

查看试题解析
7. 如图，在 $△ A B C$ 中， $∠ B = 90 °$ ， $A B = 8 c m$ ， $B C = 6 c m$ ，动点P ， Q分别从点A ， B同时开始沿 $A B$ ， $B C$ 运动（运动方向如图所示），点P的速度为 $1 c m / s$ ，点Q的速度为 $2 c m / s$ ，当点Q移动到点C时，两点同时停止运动，设运动的时间为 $t s$ ，当 $△ P B Q$ 的面积为 $12 c m^{2}$ 时，则可列方程为（）

A、 $\frac{1}{2} t (8 - t) = 12$ B、 $2 t (8 - t) = 12$ C、 $\frac{1}{2} t (8 - 2 t) = 12$ D、 $t (8 - t) = 12$

查看试题解析
8. 如图，四边形ABCD是⊙O的外切四边形，且AB＝10，CD＝12，则四边形ABCD的周长为（　　）

A、44 B、42 C、46 D、47

查看试题解析
9. 如图，已知等边三角形 $A B C$ 的边长为2，以边 $B C$ 为直径的 $⊙ O$ 交 $A B$ 于点D ，则阴影部分的面积是（）

A、 $π$ B、 $\frac{π}{3}$ C、 $\frac{2 π}{3}$ D、 $\frac{π}{6}$

查看试题解析
10. 二次函数 $y = a x^{2} + b x + c$ （a ， b ， c是常数， $a \neq 0$ ）的自变量x与函数值y的部分对应值如下表：
x
…
$- 2$
$- 1$
0
1
2
…
$y = a x^{2} + b x + c$
…
t
m
$- 2$
$- 2$
n
…
且当 $x = - \frac{1}{2}$ 时，与其对应的函数值 $y > 0$ ．有下列结论：① $a b c < 0$ ；② $- 2$ 和3是关于x的方程 $a x^{2} + b x + c = t$ 的两个根；③ $0 < m + n < \frac{20}{3}$ ．其中，正确结论的个数是（　　）

A、0 B、1 C、2 D、3

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分．请将最简答案填写在答题卡相应位置）

11. 在平面直角坐标系中，若点 $P (1 ， - 5)$ 与点 $Q (- 1 ， m)$ 关于原点对称，则m的值是．

查看试题解析
12. 某试验小组做了可转动转盘（如图），想求当转盘停止转动后，“指针落在灰色区域内”的概率，试验数据如下表：
试验次数n
20
40
60
80
100
1000
“指针落在灰色区域内”的次数m
6
11
15
21
25
251
“指针落在灰色区域内”的频率 $\frac{m}{n}$
0.3
0.275
0.25
0.2625
0.25
0.251
根据表格，可以估计出转动转盘一次，当转盘停止转动后，“指针落在灰色区域内”的概率约是．（结果精确到0.01）

查看试题解析
13. 如图，用若干个全等的正五边形排成圆环状，图中所示的是其中3个正五边形的位置．要完成这一圆环排列，共需要正五边形的个数是个．

查看试题解析
14. 在为期3天的广安市第五届运动会（青少年组）三人制篮球比赛中，某同学进行了一次投篮，篮球准确落入篮框内，建立如图所示的平面直角坐标系，篮球的运行轨迹可看作抛物线 $y = - x^{2} + 2 x + 2.6$ 的一部分，则篮球在空中运行的最大高度为 $m$ ．

查看试题解析
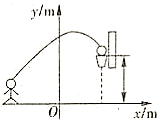15. 如图，在平面直角坐标系中，线段 $O A$ 与x轴正方向的夹角为 $45 °$ ，且 $O A = 2$ ，若将线段 $O A$ 绕点O沿逆时针方向旋转 $105 °$ 得到线段 $O A^{^{'}}$ ，则此时点 $A^{'}$ 的坐标为．

查看试题解析
16. 已知a是方程 $x^{2} - 2024 x + 1 = 0$ 一个根，则 $a^{2} - 2023 a + \frac{2024}{a^{2} + 1}$ 的值为．

查看试题解析

三、解答题（本大题共4小题，第17小题5分，第18、19、20小题各6分，共23分）

17. 解方程： ${(x + 6)}^{2} = 7 (x + 6)$ ．

查看试题解析
18. 如图，在 $△ A B C$ 中，以 $A B$ 为直径的 $⊙ O$ 交 $A C$ 于点D ．若 $A B = 6$ ， $∠ A = 54 °$ ，求劣弧 $\overset{⌢}{A D}$ 的长．（结果保留 $π$ ）

查看试题解析
19. 已知抛物线 $y = - \frac{1}{4} x^{2} + x + 5$ ．

(1)、求抛物线的开口方向和对称轴；

(2)、当 $- 1 \leq x \leq 3$ 时，求y的取值范围．

查看试题解析
20. 如图，在 $△ A B C$ 中， $B A = B C$ ，以 $A B$ 为直径作 $⊙ O$ ，交 $A C$ 于点 $D$ ，连接 $D B$ ，过点 $D$ 作 $D E ⊥ B C$ ，垂足为 $E$ ．

(1)、求证： $A D = C D$ ；

(2)、求证： $D E$ 为 $⊙ O$ 的切线．

查看试题解析

四、实践应用题（本大题共4小题，第21小题6分，第22、23、24小题各8分，共30分）

21. 如图，在 $4 \times 4$ 的方格中，有4个小方格被涂黑成“L形”．

(1)、在图1中再涂黑4格，使新涂黑的图形与原来的“L形”关于点O成中心对称；

(2)、在图2中再涂黑4格，使新涂黑的图形与原来的“L形”所组成的新图形既是轴对称图形又是中心对称图形．

查看试题解析
22. 寒假期间，小赵的爸爸准备带小赵去广安旅游．由于时间关系，原计划去的华蓥山和天意谷只能去其中一个，现决定用抽扑克牌的方式来决定，具体方法如下：把四张牌面数字分别是2，3，4，5的扑克牌背面向上放置于桌面上，洗匀后，小赵先从中任意抽出一张，然后爸爸再从剩下的三张中任意抽出一张，如果两人的牌面数字之和大于7，就去华蓥山；否则，就去天意谷．

(1)、如果小赵抽出的牌面数字是4，那么他们去华蓥山的概率为；

(2)、请利用画树状图或列表的方法分析他们去华蓥山和天意谷哪个地方的概率大．

查看试题解析
23. 如图1，圆形拱门屏风是家庭中常见的装饰隔断，既美观又实用，彰显出中国元素的韵味．如图2是一款拱门的示意图，其中C为 $A B$ 的中点，D为拱门最高点，线段 $C D$ 经过圆心O ，已知拱门的半径为 $1.5 m$ ，拱门最下端 $A B = 1.8 m$ ．

(1)、求拱门最高点D到地面的距离；

(2)、现需要给房间内搬进一张长和宽均为 $2 m$ 、高为 $1.2 m$ 的桌子，已知搬桌子的两名工人在搬运时所抬高度相同，且高度为 $0.5 m$ ，判断搬运该桌子时是否能够通过拱门．（参考数据： $\sqrt{5} \approx 2.236$ ）

查看试题解析
24. 在国家积极政策的鼓励下，环保意识日渐深入人心，新能源汽车的市场需求逐年上升．

(1)、某汽车企业2020年到2022年这两年新能源汽车的销售总量增长了96%．求该汽车企业这两年新能源汽车销售总量的平均年增长率；

(2)、某汽车企业下属的一个专卖店经销一款进价为15万元/辆的新能源汽车，经销一段时间后发现：当该款汽车售价定为25万元/辆时，平均每周售出8辆；售价每降低0.5万元，平均每周多售出1辆．若该店计划下调售价使平均每周的销售利润为96万元，并且尽量让利于顾客，求下调后每辆汽车的售价．

查看试题解析

五、推理论证题（9分）

25. 如图1，P为正方形 $A B C D$ 内一点， $P A ： P B ： P C = 1 ： 2 ： 3$ ，求 $∠ A P B$ 的度数．
小明同学的想法是：不妨设 $P A = x$ ， $P B = 2 x$ ， $P C = 3 x$ ，设法把 $P A ， P B ， P C$ 相对集中，于是他将 $△ B C P$ 绕点B顺时针旋转 $90 °$ 得到 $△ B A E$ （如图2），然后连接 $P E$ ，问题得以解决．

(1)、求出图2中 $∠ A P B$ 的度数；

(2)、请你参考小明同学的方法，解答下列问题：
如图3，P是等边三角形 $A B C$ 内一点， $P A ： P B ： P C = 3 ： 4 ： 5$ ，求 $∠ A P B$ 的度数．

查看试题解析

六、拓展探究题（10分）

26. 综合与探究
如图，抛物线 $y = a x^{2} + 2 x + c$ 经过 $A (- 1 ， 0)$ ， $C (0 ， 3)$ 两点，与x轴的另一个交点为点B ，点D在y轴上，且 $O B = 3 O D$ ．

(1)、求该抛物线的函数表达式；

(2)、设该抛物线上的一个动点P的横坐标为t ，当 $0 < t < 3$ 时，求四边形 $C D B P$ 的面积S与t的函数关系式，并求出S的最大值；

(3)、设该抛物线上的一个动点P的横坐标为t ，点Q在直线 $B C$ 上，若以 $C D$ 为边，点 $C 、 D 、 Q 、 P$ 为顶点的四边形是平行四边形，请求出所有符合条件的点P的坐标．

查看试题解析

x	…	$- 2$	$- 1$	0	1	2	…
$y = a x^{2} + b x + c$	…	t	m	$- 2$	$- 2$	n	…

试验次数n	20	40	60	80	100	1000
“指针落在灰色区域内”的次数m	6	11	15	21	25	251
“指针落在灰色区域内”的频率 $\frac{m}{n}$	0.3	0.275	0.25	0.2625	0.25	0.251