四川省绵阳市游仙区2023-2024学年九年级上学期数学期末考试试卷
试卷更新日期:2024-04-16 类型:期末考试
一、选择题(每小题3分,满分36分)
-
1. 下列事件是必然事件的是( )A、抛出的篮球会下落 B、抛掷一个均匀硬币,正面朝上 C、打开电视机,正在播广告 D、买一张电影票,座位号是奇数号2. 围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史.下列由黑白棋子摆成的图案是中心对称图形的是( )A、
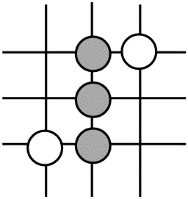
B、
B、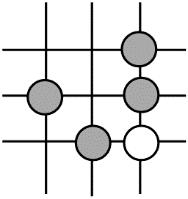
C、
C、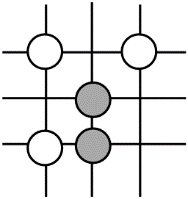
D、
D、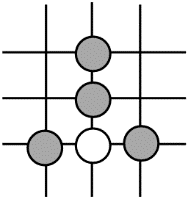
3. 下列是一元二次方程的是( )A、 B、 C、 D、4. 已知抛物线与轴的两个交点在两旁,则关于的方程的根的情况是( )A、有两个正数根 B、有两个负数根 C、有一个正根和一个负根 D、无实数根5. 如图,AB为 的直径,P为BA延长线上的一点,D在 上(不与点A,点B重合),连结PD交 于点C,且PC=OB.设 ,下列说法正确的是( )
3. 下列是一元二次方程的是( )A、 B、 C、 D、4. 已知抛物线与轴的两个交点在两旁,则关于的方程的根的情况是( )A、有两个正数根 B、有两个负数根 C、有一个正根和一个负根 D、无实数根5. 如图,AB为 的直径,P为BA延长线上的一点,D在 上(不与点A,点B重合),连结PD交 于点C,且PC=OB.设 ,下列说法正确的是( )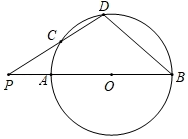 A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则6. 从十二边形的一个顶点引对角线,可把这个多边形分成( )个三角形.A、10 B、11 C、12 D、137. 如图, , 是的切线,A , B是切点,若 , , 则的长为( )
A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则6. 从十二边形的一个顶点引对角线,可把这个多边形分成( )个三角形.A、10 B、11 C、12 D、137. 如图, , 是的切线,A , B是切点,若 , , 则的长为( ) A、 B、 C、 D、8. 如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置.若四边形AECF的面积为36,DE=2,则AF的长为( )
A、 B、 C、 D、8. 如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置.若四边形AECF的面积为36,DE=2,则AF的长为( ) A、6 B、 C、8 D、9. 若关于x的方程ax2﹣(3a+1)x+2(a+1)=0有两个不相等的实数根x1 , x2 , 且有x1﹣x1x2+x2=1﹣a,则a的值是( )A、﹣1 B、1 C、1或﹣1 D、210.
A、6 B、 C、8 D、9. 若关于x的方程ax2﹣(3a+1)x+2(a+1)=0有两个不相等的实数根x1 , x2 , 且有x1﹣x1x2+x2=1﹣a,则a的值是( )A、﹣1 B、1 C、1或﹣1 D、210.如图,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)交于A,B两点,且点A的横坐标是﹣2,点B的横坐标是3,则以下结论:
①抛物线y=ax2(a≠0)的图象的顶点一定是原点;
②x>0时,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)的函数值都随着x的增大而增大;
③AB的长度可以等于5;
④△OAB有可能成为等边三角形;
⑤当﹣3<x<2时,ax2+kx<b,
其中正确的结论是( )
 A、①②④ B、①②⑤ C、②③④ D、③④⑤11. 如图,在平面直角坐标系中,边长为 的正方形 的边 轴,顶点 的坐标为 .二次函数 的图象的顶点在正方形 的边上运动,则 的值可以( ).
A、①②④ B、①②⑤ C、②③④ D、③④⑤11. 如图,在平面直角坐标系中,边长为 的正方形 的边 轴,顶点 的坐标为 .二次函数 的图象的顶点在正方形 的边上运动,则 的值可以( ).
 A、 B、 C、 D、12. 如图,边长为12的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB , 将线段BM绕点B逆时针旋转60°得到BN , 连结HN . 则在点M运动过程中,线段HN长度的最小值是( )
A、 B、 C、 D、12. 如图,边长为12的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB , 将线段BM绕点B逆时针旋转60°得到BN , 连结HN . 则在点M运动过程中,线段HN长度的最小值是( ) A、6 B、3 C、2 D、1.5
A、6 B、3 C、2 D、1.5二、填空题(每小题4分,满分24分)
-
13. 已知函数的图象是抛物线,则 .14. 在一个不透明的空袋子里,放入分别标有数字1,2,3,5的四个小球(除数字外其他完全相间),从中随机摸出2个小球,摸到的2个小球的数字之和恰为偶数的概率是 .15. 已知圆锥的底面半径为 , 它的侧面积是 , 则这个圆锥的母线长为 .16. 某商场将进价为30元的台灯以单价40元售出,平均每月能售出600个.调查表明:这种台灯的单价每上涨1元,其销售量将减少10个.为实现平均每月10000元的销售利润,从消费者的角度考虑,商场对这种台灯的售价应定为元.17. 二次函数的图像如图,若一元二次方程有实数根,则的最小值为.
 18. 如图,∠BAC=60°,∠ABC=45°,AB= , D是线段BC上的一个动点,以AD为直径画⊙O分别交AB , AC于E , F , 连接EF , 则线段EF长度的最小值为 .
18. 如图,∠BAC=60°,∠ABC=45°,AB= , D是线段BC上的一个动点,以AD为直径画⊙O分别交AB , AC于E , F , 连接EF , 则线段EF长度的最小值为 .
三、解答题(满分90分)
-
19. 已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
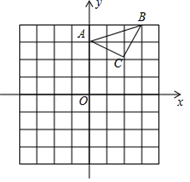 (1)、画出△ABC向下平移4个单位,再向左平移1个单位得到的△A1B1C1 , 并直接写出C1点的坐标;(2)、画出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2 , 并直接写出C2点的坐标;(3)、请求出(2)中△ABC旋转过程中所扫过的面积为 .20. 某中学准备举办一次演讲比赛,每班限定两人报名,初三(1)班的三位同学(两位女生,一位男生)都想报名参加,班主任李老师设计了一个摸球游戏,利用已学过的概率知识来决定谁去参加比赛,游戏规则如下:在一个不透明的箱子里放3个大小质地完全相同的乒乓球,在这3个乒乓球上分别写上 、 、 (每个字母分别代表一位同学,其中 、 分别代表两位女生, 代表男生),搅匀后,李老师从箱子里随机摸出一个乒乓球,不放回,再次搅匀后随机摸出第二个乒乓球,根据乒乓球上的字母决定谁去参加比赛。(1)、求李老师第一次摸出的乒乓球代表男生的概率;(2)、请用列表或画树状图的方法求恰好选定一名男生和一名女生参赛的概率.21. 如图,若二次函数的图象与轴交于 , 两点(点在点的左侧),与轴交于点.
(1)、画出△ABC向下平移4个单位,再向左平移1个单位得到的△A1B1C1 , 并直接写出C1点的坐标;(2)、画出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2 , 并直接写出C2点的坐标;(3)、请求出(2)中△ABC旋转过程中所扫过的面积为 .20. 某中学准备举办一次演讲比赛,每班限定两人报名,初三(1)班的三位同学(两位女生,一位男生)都想报名参加,班主任李老师设计了一个摸球游戏,利用已学过的概率知识来决定谁去参加比赛,游戏规则如下:在一个不透明的箱子里放3个大小质地完全相同的乒乓球,在这3个乒乓球上分别写上 、 、 (每个字母分别代表一位同学,其中 、 分别代表两位女生, 代表男生),搅匀后,李老师从箱子里随机摸出一个乒乓球,不放回,再次搅匀后随机摸出第二个乒乓球,根据乒乓球上的字母决定谁去参加比赛。(1)、求李老师第一次摸出的乒乓球代表男生的概率;(2)、请用列表或画树状图的方法求恰好选定一名男生和一名女生参赛的概率.21. 如图,若二次函数的图象与轴交于 , 两点(点在点的左侧),与轴交于点. (1)、求顶点坐标和 , 两点的坐标;(2)、若为二次函数图象上一点且 , 求点的坐标.22. 如图,在Rt△ABC中, , D为AB的中点,以CD 为直径的分别交AC , BC于点E , F两点,过点F作于点G .
(1)、求顶点坐标和 , 两点的坐标;(2)、若为二次函数图象上一点且 , 求点的坐标.22. 如图,在Rt△ABC中, , D为AB的中点,以CD 为直径的分别交AC , BC于点E , F两点,过点F作于点G . (1)、试判断FG与的位置关系,并说明理由;(2)、若 , , 求FG的长.23. 完成下列各题
(1)、试判断FG与的位置关系,并说明理由;(2)、若 , , 求FG的长.23. 完成下列各题 (1)、问题的提出:如图1,中, , 求证: .(2)、知识的运用:如图2,四边形是正方形, , , 点是边上一点, , 且 , 连 . 求的度数.(3)、拓展与延伸:如图3,四边形中, , , , 为四边形边上一点,连 , 若 , 且 , 探究与的数量关系.直接写出结果,不需说明理由.
(1)、问题的提出:如图1,中, , 求证: .(2)、知识的运用:如图2,四边形是正方形, , , 点是边上一点, , 且 , 连 . 求的度数.(3)、拓展与延伸:如图3,四边形中, , , , 为四边形边上一点,连 , 若 , 且 , 探究与的数量关系.直接写出结果,不需说明理由.

 图2
图2