四川省达州市重点中学2023-2024学九年级上学期数学期中考试试卷

试卷更新日期：2024-04-16 类型：期中考试

进入出卷网下载

一、选择题：(每小题4分，共40分。)

1. 下列方程中是关于x的一元二次方程的是（）

A、 $x^{2} + \frac{1}{x^{2}} = 0$ B、 $a^{2} + b x + c = 0$ C、 $(x - 1) (x + 2) = 1$ D、 $3 x^{2} - 2 x y - 5 y^{2} = 0$

查看试题解析
2. 已知四边形ABCD是平行四边形，对角线AC与BD相交于点O，下列结论中不正确的是（　　）

A、当AB=BC时，四边形ABCD是菱形 B、当AC⊥BD时，四边形ABCD是菱形 C、当OA=OB时，四边形ABCD是矩形 D、当∠ABD=∠CBD时，四边形ABCD是矩形

查看试题解析
3. 端午节吃粽子是中华民族的传统习俗，妈妈买了2只红豆粽、3只碱水粽、5只咸肉粽，粽子除内部馅料不同外其他均相同，小颖随意吃一个，吃到红豆粽的概率是(　　)

A、 $\frac{1}{10}$ B、 $\frac{1}{5}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
4. 如图，正方形ABCD的边长是4，∠DAC的平分线交DC于点E，若点P、Q分别是AD和AE上的动点，则DQ+PQ的最小值（　　）

A、 $2 \sqrt{2}$ B、2 C、4 D、 $4 \sqrt{2}$

查看试题解析
5. 已知△ABC如图所示，则下列4个三角形中，与△ABC相似的是（）

A、 B、 C、 D、

查看试题解析
6. 若 $\frac{a}{5} = \frac{b}{7} = \frac{c}{8}$ ，且 $3 a - 2 b + c = 3$ ，则 $2 a + 4 b - 3 c$ 的值是（）

A、14 B、42 C、7 D、 $\frac{14}{3}$

查看试题解析
7. 某城市前年底已有绿化面积300公顷，经过两年绿化，绿化面积逐年增加，到今年底增加到363公顷。设绿化面积平均每年的增长率为 $x$ ，由题意，所列方程正确的是（）

A、 $300 (1 + x) = 363$ B、 $300 (1 + x)_{}^{2} = 363$ C、 $300 (1 + 2 x) = 363$ D、 $363 (1 - x)_{}^{2} = 300$

查看试题解析
8. 张华在一次数学活动中，利用“在面积一定的矩形中，正方形的周长最短”的结论，推导出“式子x+ $\frac{1}{x}$ （x＞0）的最小值是2”．其推导方法如下：在面积是1的矩形中设矩形的一边长为x ，则另一边长是 $\frac{1}{x}$ ，矩形的周长是2（x+ $\frac{1}{x}$ ）；当矩形成为正方形时，就有x= $\frac{1}{x}$ （x＞0），解得x=1，这时矩形的周长2（x+ $\frac{1}{x}$ ）=4最小，因此x+ $\frac{1}{x}$ （x＞0）的最小值是2．模仿张华的推导，你求得式子 $\frac{x_{}^{2} + 25}{x}$ （x＞0）的最小值是（）

A、10 B、5 C、15 D、20

查看试题解析
9. 如图，点 $C$ 是线段 $A B$ 的黄金分割点（ $A C > B C$ ），下列结论错误的是（）

A、 $\frac{A C}{A B} = \frac{B C}{A C}$ B、 $B C^{2} = A C • A B$ C、 $\frac{A C}{A B} = \frac{\sqrt{5} - 1}{2}$ D、 $\frac{B C}{A C} \approx 0.618$

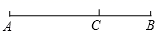查看试题解析
10. .如图，在△ABC中∠A=60°，BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，连接PM，PN，则下列结论：①PM=PN；②；③△PMN为等边三角形；④当∠ABC=45°时，BN=PC．其中正确的个数是（　　）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题：（本大题共6小题，每小题4分，满分24分。）

11. 菱形的两条对角线长分别是方程x²-14x+48=0的两实根，则菱形的面积为。

查看试题解析
12. 已知关于x的方程 x²-mx-6=0 的一个根为2，则m= ，另一根是.

查看试题解析
13. 关于x的方程 $k x^{2} - 2 x + 1 = 0$ 有两个不相等的实数根，则k的取值范围是。

查看试题解析
14. 如图，在△ABC中，DE∥BC， $\frac{D E}{B C} = \frac{2}{3}$ ， △ADE的面积为8，则△ABC的面积为.

查看试题解析
15. 将一副三角尺如图所示叠放在一起，则 $\frac{A E}{E D}$ 的值是．

查看试题解析
16. 在平面直角坐标系中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2）．延长CB交x轴于点A₁ ，作正方形A₁B₁C₁C；延长C₁B₁交x轴于点A₂ ，作正方形A₂B₂C₂C₁…按这样的规律进行下去，第2014个正方形的面积为

查看试题解析

三、解答题：（本大题4个小题，共86分）解答时每小题需给出必要的演算过程或推理步骤。

17. 解方程：

(1)、2x²-2x-1=0

(2)、(x－2)²－3(x－2)＝0．

查看试题解析
18. 如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别为A（-1，2），B（-3，4）C（-2，6）

(1)、画出△ABC绕点A顺时针旋转90°后得到的△A₁B₁C₁

(2)、以原点O为位似中心，画出将△A₁B₁C₁三条边放大为原来的2倍后的△A₂B₂C₂ ．

查看试题解析
19. 已知关于x的一元二次方程x²+（2k-1）x-k-1=0．

(1)、试判断此一元二次方程根的存在情况；

(2)、若方程有两个实数根x₁和x₂ ，且满足 $\frac{1}{x_{1}^{}} + \frac{1}{x_{2}^{}} = 1$ ，求k的值．

查看试题解析
20. 第三届亚洲沙滩运动会服务中心要在某校选拔一名志愿者．经笔试、面试，结果小明和小颖并列第一．评委会决定通过抓球来确定人选．抓球规则如下：在不透明的布袋里装有除颜色之外均相同的2个红球和1个绿球，小明先取出一个球，记住颜色后放回，然后小颖再取出一个球．若取出的球都是红球，则小明胜出；若取出的球是一红一绿，则小颖胜出．你认为这个规则对双方公平吗？请用列表法或画树状图的方法进行分析．

查看试题解析
21. 某水果批发商场经销一种水果，如果每千克盈利10元，每天可售出400千克．经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克．

(1)、若商场只要求保证每天的盈利为4320元，同时又可使顾客得到实惠，每千克应涨价多少元？

(2)、若该商场经理想让这种水果每天的盈利为4600元，商场经理的想法能实现吗？如果能请求出每千克应涨价多少元，如果不能请说明理由。

查看试题解析
22. 如图，△ABC中，AB=AC，AD是∠BAC的角平分线，点O为AB的中点，连接DO并延长到点E，使OE=OD，连接AE，BE．

(1)、求证：四边形AEBD是矩形；

(2)、当△ABC满足什么条件时，矩形AEBD是正方形，并说明理由．

查看试题解析
23. 如图，在△ABC中，∠C=90°，AD是∠CAB的角平分线，BE⊥AE，垂足为点E．
求证：BE²=DE•AE．

查看试题解析
24. 阅读理解：
如图1，在四边形ABCD的边AB上任取一点E（点E不与点A、点B重合），分别连接ED，EC，可以把四边形ABCD分成三个三角形，如果其中有两个三角形相似，我们就把E叫做四边形ABCD的边AB上的相似点；如果这三个三角形都相似，我们就把E叫做四边形ABCD的边AB上的强相似点．解决问题：

(1)、如图1，∠A=∠B=∠DEC=55°，试判断点E是否是四边形ABCD的边AB上的相似点，并说明理由；

(2)、如图2在矩形ABCD中，AB=5，BC=2，且A，B，C，D四点均在正方形网格（网格中每个小正方形的边长为1）的格点（即每个小正方形的顶点）上，试在图2中画出矩形ABCD的边AB上的一个强相似点E；

(3)、拓展探究：
如图3，将矩形ABCD沿CM折叠，使点D落在AB边上的点E处．若点E恰好是四边形ABCM的边AB上的一个强相似点，当BC= $\sqrt{3}$ 时，试求出AB的值．

查看试题解析
25. 如图，在平面直角坐标系内，已知点A（0，6）、点B（8，0），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动，同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动，设点P、Q移动的时间为t秒．

(1)、求直线AB的解析式；

(2)、当t为何值时，△APQ与△AOB相似。

(3)、当t为何值时，△APQ的面积为 $\frac{16}{5}$ 个平方单位。

查看试题解析

四川省达州市重点中学2023-2024学九年级上学期数学期中考试试卷

一、 选择题：(每小题4分，共40分。)

二、 填空题：（本大题共6小题，每小题4分，满分24分。）

三、解答题：（本大题4个小题，共86分）解答时每小题需给出必要的演算过程或推理步骤。

一、选择题：(每小题4分，共40分。)

二、填空题：（本大题共6小题，每小题4分，满分24分。）