四川省广元市旺苍县2023-2024学年七年级上学期数学期末考试试卷
试卷更新日期:2024-04-16 类型:期末考试
一、单选题(下列每小题给出的四个选项中,只有一个是符合题意的.每小题3分,共30分)
-
1. 如果向东走2米记作米,那么向西走3米记作( )A、米 B、米 C、米 D、米2. 下列图形中,不是正方体的展开图的是( )
A、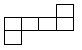 B、
B、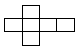 C、
C、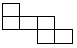 D、
D、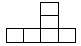 3. 2023年2月10号,神舟十五号航天员乘组圆满完成了他们的首次出舱任务,飞船的速度约为每小时 28000000 米, 28000000用科学记数法表示应为( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 已知 , 则的补角等于( )A、 B、 C、 D、6. 若是关于x的方程的解,则a的值为( )A、7 B、1 C、 D、7. 如图,已知线段 ,点N在AB上, ,M是AB中点,那么线段MN的长为
3. 2023年2月10号,神舟十五号航天员乘组圆满完成了他们的首次出舱任务,飞船的速度约为每小时 28000000 米, 28000000用科学记数法表示应为( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 已知 , 则的补角等于( )A、 B、 C、 D、6. 若是关于x的方程的解,则a的值为( )A、7 B、1 C、 D、7. 如图,已知线段 ,点N在AB上, ,M是AB中点,那么线段MN的长为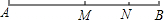 A、6cm B、5cm C、4cm D、3cm8. 我国古代数学名著《张丘建算经》中记载:“今有清酒一斗值粟十斗,醑酒一斗值粟三斗,今持粟三斛,得酒五斗,问清、醑酒各几何?”意思是:现在一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清、醑酒各几斗,设清酒有x斗,那么可列方程为( )A、 B、 C、 D、9. 已知下列一组数:1, ,…;用代数式表示第n个数,则第n个数是( )
A、6cm B、5cm C、4cm D、3cm8. 我国古代数学名著《张丘建算经》中记载:“今有清酒一斗值粟十斗,醑酒一斗值粟三斗,今持粟三斛,得酒五斗,问清、醑酒各几何?”意思是:现在一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清、醑酒各几斗,设清酒有x斗,那么可列方程为( )A、 B、 C、 D、9. 已知下列一组数:1, ,…;用代数式表示第n个数,则第n个数是( )
A、 B、 C、 D、10. 已知有理数a , b满足∶ . 如图,在数轴上,点O是原点,点A所对应的数是a , 线段在直线上运动(点B在点C的左侧),且 , 下列结论:
① , ; ②当点B与点O重合时,;③当点C与点A重合时, 若点P是线段延长线上的点, 则;④在线段运动过程中,若M为线段的中点,N 为线段的中点,则线段的长度不变. 其中正确的有( )
A、1个 B、2个 C、3个 D、4个二、填空题(把正确答案直接写在答题卡对应题目的横线上,每小题4分,共24分)
-
11. 比较大小: (填 “” 或 “” 或 “” )12. 已知单项式与是同类项,那么 m-2n=.13. 计算: .14. 已知关于x的一元一次方程的解是正整数,则所有满足题意的整数k的和是 .15. 代数式的值为7,则代数式的值是16. 如图,点、是线段上两点,、分别是线段、的中点,给出下列结论:①若 , 则;②;则;③;其中正确的有(请填写序号)

三、解答题(要求写出必要的解答步骤或证明过程.共96分)
-
17. 计算:(1)、;(2)、 .18. 先化简, 在求值∶ , 其中x是最大的负整数,y是最小的正偶数.19. 解方程:(1)、(2)、20. 有理数a、 b、 c在数轴上的位置如下图所示:
 (1)、比较、 b、 c的大小(用“”连接) ;(2)、化简 .21. 当 , 时,求的值.一名同学做题时,错把看成 , 但结果也正确,且计算过程无误,求的值.22. 如图,O是直线上一点, , 平分 , . 求的度数.
(1)、比较、 b、 c的大小(用“”连接) ;(2)、化简 .21. 当 , 时,求的值.一名同学做题时,错把看成 , 但结果也正确,且计算过程无误,求的值.22. 如图,O是直线上一点, , 平分 , . 求的度数. 23. 出租车司机张师傅某一天下午的营运全是在东西走向的新华街进行的,并在电影院接到第一位乘客,假定向东为正,向西为负,他这天下午的行车记录(单位:)如下∶ , , , , , , .(1)、最后一位乘客下车时,张师傅在电影院的东方还是西方? 此时距电影院多少千米?(2)、若该出租车的耗油量为 , 则这天下午该出租车共耗油多少升?24. 为了保障广大师生的身体健康,某校初三返校复学后,采购了甲种免洗消毒液20瓶,乙种免洗消毒液30瓶,已知甲消毒液的单价比乙贵10元,两种消毒液的采购费用相等.(1)、甲种消毒液和乙种消毒液的单价分别是多少元?(2)、初一和初二年级复学后,学校再次采购甲、乙两种消毒液,甲消毒液的采购数量是第一次采购数量的2倍,采购单价比第一次提高了 , 乙消毒液比第一次多采购了瓶,单价与第一次采购单价相同,结果第二次采购的总费用是第一次总费用的2倍,求的值.25. 若有理数p , q满足 , 则称“ p , q”为“等效有理数对”,如:“2,2”,因为 , 所以“2 ,2”是“等效有理数对”.(1)、通过计算判断“3 , ”是不是“等效有序数对” ;(2)、若“ , 4”是“等效有理数对”, 求x的值;(3)、已知“p , q”是“等效有理数对”, 求代数式的值.26. 如图,A , B分别为数轴上的两点,点A对应的数是 , 点B对应的数是8.现有点P从点A出发,以4个单位长度/秒的速度向右运动,同时另一点Q从点B出发,以1个单位长度/秒的速度向右运动,设运动时间为秒.
23. 出租车司机张师傅某一天下午的营运全是在东西走向的新华街进行的,并在电影院接到第一位乘客,假定向东为正,向西为负,他这天下午的行车记录(单位:)如下∶ , , , , , , .(1)、最后一位乘客下车时,张师傅在电影院的东方还是西方? 此时距电影院多少千米?(2)、若该出租车的耗油量为 , 则这天下午该出租车共耗油多少升?24. 为了保障广大师生的身体健康,某校初三返校复学后,采购了甲种免洗消毒液20瓶,乙种免洗消毒液30瓶,已知甲消毒液的单价比乙贵10元,两种消毒液的采购费用相等.(1)、甲种消毒液和乙种消毒液的单价分别是多少元?(2)、初一和初二年级复学后,学校再次采购甲、乙两种消毒液,甲消毒液的采购数量是第一次采购数量的2倍,采购单价比第一次提高了 , 乙消毒液比第一次多采购了瓶,单价与第一次采购单价相同,结果第二次采购的总费用是第一次总费用的2倍,求的值.25. 若有理数p , q满足 , 则称“ p , q”为“等效有理数对”,如:“2,2”,因为 , 所以“2 ,2”是“等效有理数对”.(1)、通过计算判断“3 , ”是不是“等效有序数对” ;(2)、若“ , 4”是“等效有理数对”, 求x的值;(3)、已知“p , q”是“等效有理数对”, 求代数式的值.26. 如图,A , B分别为数轴上的两点,点A对应的数是 , 点B对应的数是8.现有点P从点A出发,以4个单位长度/秒的速度向右运动,同时另一点Q从点B出发,以1个单位长度/秒的速度向右运动,设运动时间为秒. (1)、直接写出A , B两点之间的距离;(2)、当时,求P、Q两点之间的距离;(3)、在运动过程中,线段、、中是否会有两条线段相等?若有,请求出此时的值;若没有,请说明理由.
(1)、直接写出A , B两点之间的距离;(2)、当时,求P、Q两点之间的距离;(3)、在运动过程中,线段、、中是否会有两条线段相等?若有,请求出此时的值;若没有,请说明理由.