湖南省长沙市明德教育集团2023-2024学年九年级上学期数学期末考试试卷
试卷更新日期:2024-04-16 类型:期末考试
一、选择题(在下列各题的四个选项中,只有一项是正确答案,请在答题卡中填涂符合题
-
1. 下列实数中,为有理数的是( )A、 B、π C、 D、12. 下列立体图形中,主视图是圆的是( )A、
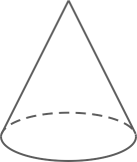 B、
B、 C、
C、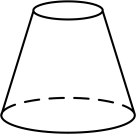 D、
D、 3. 近期感染肺炎支原体学生骤增,引发了人们的关注和担心.据了解,支原体没有细胞壁,只有细胞膜,所以支原体的形态可以随机变化,是目前发现的能在无生命培养基中生长繁殖的最小最简单的细胞,直径约为0.0000001m . 把0.0000001可以用科学记数法表示为( )A、1×10﹣7 B、1×10﹣9 C、10×10﹣8 D、100×10﹣64. 下列运算正确的是( )A、a2+a3=a5 B、a6÷a3=a2 C、(﹣a4)3=﹣a12 D、(a﹣b)2=a2﹣b25. 2023年12月6日,第十九届中国中学生篮球锦标赛落下帷幕.长沙市明德中学男子篮球队夺得第十九届CSBA男子组全国总冠军!在“无体育不明德,无运动不青春”理念下,某校组织了篮球兴趣小组,共40名学生进行定期训练,他们的年龄分布如下表:他们年龄的中位数是( )
3. 近期感染肺炎支原体学生骤增,引发了人们的关注和担心.据了解,支原体没有细胞壁,只有细胞膜,所以支原体的形态可以随机变化,是目前发现的能在无生命培养基中生长繁殖的最小最简单的细胞,直径约为0.0000001m . 把0.0000001可以用科学记数法表示为( )A、1×10﹣7 B、1×10﹣9 C、10×10﹣8 D、100×10﹣64. 下列运算正确的是( )A、a2+a3=a5 B、a6÷a3=a2 C、(﹣a4)3=﹣a12 D、(a﹣b)2=a2﹣b25. 2023年12月6日,第十九届中国中学生篮球锦标赛落下帷幕.长沙市明德中学男子篮球队夺得第十九届CSBA男子组全国总冠军!在“无体育不明德,无运动不青春”理念下,某校组织了篮球兴趣小组,共40名学生进行定期训练,他们的年龄分布如下表:他们年龄的中位数是( )年龄/岁
15
16
17
18
人数
7
18
12
3
A、15 B、16 C、17 D、186. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、 B、
B、 C、
C、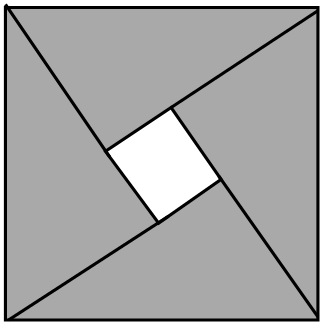 D、
D、 7. 我国古代《孙子算经》记载“多人共车”问题:“今有三人共车,二车空;二人共车,九人步问人与车各几何?”意思是说“每三人共乘一辆车,最终剩余2辆车;每2人共乘一辆车,最终有9人无车可乘.问人和车的数量各是多少?”若设有x个人,则可列方程是( )A、3(x+2)=2x﹣9 B、3(x﹣2)=2x+9 C、2 D、28. 如图,AB∥CD , ∠A=125°,∠CED=60°,则∠D的度数为( )
7. 我国古代《孙子算经》记载“多人共车”问题:“今有三人共车,二车空;二人共车,九人步问人与车各几何?”意思是说“每三人共乘一辆车,最终剩余2辆车;每2人共乘一辆车,最终有9人无车可乘.问人和车的数量各是多少?”若设有x个人,则可列方程是( )A、3(x+2)=2x﹣9 B、3(x﹣2)=2x+9 C、2 D、28. 如图,AB∥CD , ∠A=125°,∠CED=60°,则∠D的度数为( ) A、45° B、60° C、65° D、75°9. 如图,四边形ABCD内接于⊙O , OC⊥弦BD , 若∠CBD=30°,则∠A的大小为( )
A、45° B、60° C、65° D、75°9. 如图,四边形ABCD内接于⊙O , OC⊥弦BD , 若∠CBD=30°,则∠A的大小为( ) A、30° B、60° C、65° D、70°10. 二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1,其中结论正确的为( )
A、30° B、60° C、65° D、70°10. 二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1,其中结论正确的为( ) A、abc<0 B、b2﹣4ac=0 C、a﹣b+c>0 D、4a+2b+c<0
A、abc<0 B、b2﹣4ac=0 C、a﹣b+c>0 D、4a+2b+c<0二、填空题(本大题共6个小题,每小题3分,共18分)
-
11. 因式分解:a2﹣4a= .12. 已知函数 , 则自变量x的取值范围是 .13. 已知关于x的一元二次方程2x2﹣kx+8=0有两个相等的实数根,则k的值是 .14. 如图,在▱ABCD中,F是边AB的中点,连接DF交AC于点E . 若CE=4,则AC的长是 .
 15. 如图点A(x , y)在反比例函数的图象上,且四边形ABCD为平行四边形,S▱ABCD=4,则k= .
15. 如图点A(x , y)在反比例函数的图象上,且四边形ABCD为平行四边形,S▱ABCD=4,则k= . 16. 如图,在平面直角坐标系中,△A'B'C'与△ABC是以原点O为位似中心的位似图形,且△A'B'C'与△ABC位似比为1:2,若A的坐标为(﹣5,6),则A'的坐标为 .
16. 如图,在平面直角坐标系中,△A'B'C'与△ABC是以原点O为位似中心的位似图形,且△A'B'C'与△ABC位似比为1:2,若A的坐标为(﹣5,6),则A'的坐标为 .
三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题6分,第22、23每小题6分,第24、25每小题6分,共72分)
-
17. 计算: .18. 先化简,后求值: , 其中x=﹣4,19. 如图所示是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横断面⊙O的圆心,支架CD与水平面AE垂直,AB=131厘米,真空集热管AB的斜面坡度为 , 另一根辅助支架DE=70厘米,∠CED=57°.
(参考数据:sin57°≈0.8,cos57°≈0.6)
 (1)、求垂直支架CE的长度.(2)、求水箱半径的长度.20. 安全无小事,长沙市教育局要求各中小学校在期末考试后进行寒假安全教育.某校在典礼上开展了休学典礼——学生安全知识竞赛,赛后发现所有参赛学生会的成绩都高于50分.为了了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分为100分)作为样本进行统计分析,得到如下不完整的统计图表,请根据图标中的信息解答下列各题:
(1)、求垂直支架CE的长度.(2)、求水箱半径的长度.20. 安全无小事,长沙市教育局要求各中小学校在期末考试后进行寒假安全教育.某校在典礼上开展了休学典礼——学生安全知识竞赛,赛后发现所有参赛学生会的成绩都高于50分.为了了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分为100分)作为样本进行统计分析,得到如下不完整的统计图表,请根据图标中的信息解答下列各题:成绩(分)
频数
频率
50<x≤60
10
a
60<x≤70
20
0.10
70<x≤80
30
0.15
80<x≤90
b
0.30
90<x≤100
80
0.40
 (1)、频数分布表中a= , 请补全频数分布直方图;(2)、若该校共有学生3200人,分数为60<x≤90分的记为良好,请你估计该校安全知识竞赛良好的学生人数;(3)、该校安全知识竞赛成绩满分共有4人,其中男生2名,女生2名,为了激励学生增强安全意识,现需要从这4人中随机抽取2人介绍学习经验,请用“列表法”或“画树状图”,求恰好选到一男一女的概率.21. 如图,菱形ABCD的对角线AC、BD相交于点O , 过点D作DE∥AC且 , 连接AE交OD于点F , 连接CE、OE .
(1)、频数分布表中a= , 请补全频数分布直方图;(2)、若该校共有学生3200人,分数为60<x≤90分的记为良好,请你估计该校安全知识竞赛良好的学生人数;(3)、该校安全知识竞赛成绩满分共有4人,其中男生2名,女生2名,为了激励学生增强安全意识,现需要从这4人中随机抽取2人介绍学习经验,请用“列表法”或“画树状图”,求恰好选到一男一女的概率.21. 如图,菱形ABCD的对角线AC、BD相交于点O , 过点D作DE∥AC且 , 连接AE交OD于点F , 连接CE、OE . (1)、求证:四边形OCED为矩形;(2)、若菱形ABCD的边长为12,∠ABC=60°,求△ADE的面积.22. 已知甲种玩具的售价为每个16元,乙种玩具的售价为每个13元.若超市购进甲种玩具10个和乙种玩具4个需要110元,购进甲种玩具7个和乙种玩具8个需要103元.(1)、求甲、乙两种玩具的进价;(2)、该超市决定每天购进甲、乙两种玩具共100个,且投入资金不少于660元又不多于688元,设购买甲种玩具m个,求有几种购买方案?哪种方案下超市获得的利润最大?最大利润为多少?23. 如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,BD平分∠ABC , 过点D作DE⊥BC交BC的延长线于点E .
(1)、求证:四边形OCED为矩形;(2)、若菱形ABCD的边长为12,∠ABC=60°,求△ADE的面积.22. 已知甲种玩具的售价为每个16元,乙种玩具的售价为每个13元.若超市购进甲种玩具10个和乙种玩具4个需要110元,购进甲种玩具7个和乙种玩具8个需要103元.(1)、求甲、乙两种玩具的进价;(2)、该超市决定每天购进甲、乙两种玩具共100个,且投入资金不少于660元又不多于688元,设购买甲种玩具m个,求有几种购买方案?哪种方案下超市获得的利润最大?最大利润为多少?23. 如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,BD平分∠ABC , 过点D作DE⊥BC交BC的延长线于点E . (1)、求证:DE是⊙O的切线;(2)、若AD=4, , 求和CE的长.24. 定义:对于两个关于x的函数,如果存在x取某一值时,两个函数的函数值相等,那么称两个函数互为“明盟函数”,其中x的值叫做这两个函数的“明盟点”,相等的函数值叫做“明盟值”.例如:对于函数y1=2x与y2=﹣x+3,当x=1时,y1=y2=2,因此,y1、y2互为“明盟函数”,x=1是这两个函数的“明盟点”,“明盟值”为2.(1)、下列函数中是y=﹣2x的“明盟函数”的有 (填序号);
(1)、求证:DE是⊙O的切线;(2)、若AD=4, , 求和CE的长.24. 定义:对于两个关于x的函数,如果存在x取某一值时,两个函数的函数值相等,那么称两个函数互为“明盟函数”,其中x的值叫做这两个函数的“明盟点”,相等的函数值叫做“明盟值”.例如:对于函数y1=2x与y2=﹣x+3,当x=1时,y1=y2=2,因此,y1、y2互为“明盟函数”,x=1是这两个函数的“明盟点”,“明盟值”为2.(1)、下列函数中是y=﹣2x的“明盟函数”的有 (填序号);①y=x﹣2;②;③y=x2+1.
(2)、已知函数y1=m(x+2)﹣3与函数y2 , 若y1与y2只存在一个“明盟点”,求m的值或取值范围;(3)、若无论n取何值,为常数)与函数y=x2﹣(2n﹣3)x+4n﹣1(n为常数,﹣1<n≤4)始终是“明盟函数”,且只有一个“明盟点”,求w的值以及“明盟值”的范围.25. 如图,⊙O为△ABC的外接圆,点B为的中点,点M为上一点,连接AM , 且∠AMB=60°,连接BM交AC于D点,过M点作⊙O的切线交AC延长线于E点. (1)、判断△ABC的形状;(2)、求证:EM=ED;(3)、已知⊙O的半径为r , 且BC平分∠EBM;
(1)、判断△ABC的形状;(2)、求证:EM=ED;(3)、已知⊙O的半径为r , 且BC平分∠EBM;①求AM•BE;
②是否为定值,若是请求出定值,若不是请说明理由.(结果用r表示)