四川省乐山市沐川县2023-2024学年七年级上学期数学期末考试试卷

试卷更新日期：2024-04-16 类型：期末考试

进入出卷网下载

一、选择题（共36分，每小题3分．本大题共12个小题，在每小题给出的四个选项中，只有一个选项是符合题目要求的，每小题选出答案后，直接将番号填在题后的括号内．）

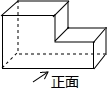
1. 2的相反数是（）

A、2 B、 $- 2$ C、 $- \frac{1}{2}$ D、4

查看试题解析
2. 下列各数比﹣3小的数是（）

A、0 B、1 C、﹣4 D、﹣1

查看试题解析
3. 原子钟是以原子的规则振动为基础的各种守时装置的统称，其中氢脉泽钟的精度达到了1700000年误差不超过1秒.数据1700000用科学记数法表示（）

A、 $17 \times 10^{5}$ B、 $1.7 \times 10^{6}$ C、 $0.17 \times 10^{7}$ D、 $1.7 \times 10^{7}$

查看试题解析
4. 如图所示的几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
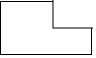5. 下列运算中，正确的是（　　）

A、 $6 + (- 6) \div (- 3) = 4$ B、 $- 2 (m - 1) = - 2 m + 1$ C、 $5 a^{2} b - 5 b a^{2} = 0$ D、 $1.901 \approx 1.9$ （精确到 $0.01$ ）

查看试题解析
6. 已知 $∠ 1 = 42 °$ ， $∠ 2$ 与 $∠ 1$ 互余，则 $∠ 2$ 的补角是（）

A、132° B、138° C、122° D、128°

查看试题解析
7. 一个正方体的展开图如图所示，如果正方体相对的两个面所标的数字均互为相反数，那么 $x + y$ 的值为（）

A、 $- 2$ B、 $- 3$ C、 $- 4$ D、 $- 5$

查看试题解析
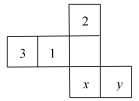8. 下列说法中，正确的是（　　）

A、 $a^{2}$ 与 $- 2 a$ 是同类项 B、单项式 $- 3 x^{2} y$ 的系数是3 C、多项式 $x y - 2 x^{2} y + y^{2}$ 是三次三项式 D、 $- 5$ 不是单项式

查看试题解析
9. 如图1，A、B两个村庄在一条河l（不计河的宽度）的两侧，现要建一座码头，使它到A、B两个村庄的距离之和最小．如图2，连接AB ，与l交于点C ，则C点即为所求的码头的位置，这样做的理由是（）

A、垂线段最短 B、两点确定一条直线 C、两点之间，线段最短 D、平行于同一条直线的两条直线平行

查看试题解析
10. 如图，快艇从P处向正北航行到A处时，向右转 $60 °$ 航行到B处，再向左转 $90 °$ 继续航行，此时的航行方向为（　　）

A、北偏西 $30 °$ B、北偏西 $60 °$ C、北偏东 $30 °$ D、北偏东 $60 °$

查看试题解析
11. 已知a、b、c在数轴上位置如图，则 $| a + b | + | a + c | - | c - b | =$ （）

A、 $0$ B、 $2 a + 2 b$ C、 $2 b - 2 c$ D、 $2 a + 2 c$

查看试题解析
12. 如图， $A B / / E F$ ， C点在EF上， $∠ E A C = ∠ E C A$ ， BC平分 $∠ D C F$ ，且 $A C ⊥ B C$ ．下列结论：
①AC平分 $∠ D C E$ ；② $A E / / C D$ ；③ $∠ 1 + ∠ B = 90 °$ ；④ $∠ B D C = 2 ∠ 1$ ．其中结论正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（共24分，每小题3分）

13. 中国是最早采用正负数表示相反意义的量的国家，一艘潜水艇向上浮50米记为 $+ 50$ 米，则向下潜15米记为米．

查看试题解析
14. 若 $- 2 x^{3} y^{m}$ 与 $x^{n} y$ 是同类项，则 $m + 2 n$ 的值为．

查看试题解析
15. 用代数式表示“ $m$ 的3倍与 $n$ 的平方的差”是．

查看试题解析
16. 如图，三条线相交于点O ， $C O ⊥ A B$ ， $∠ 1 = 52 °$ ，则 $∠ 2$ 等于．

查看试题解析
17. 已知数轴上两点A和B ，点A表示数是1，点B与A相距3个单位长度，则点B表示的数是．

查看试题解析
18. 如图，C，D是线段AB上两点，若CB= $4 ㎝$ ，DB= $7 ㎝$ ，且D是AC的中点，则AB的长等于．

查看试题解析
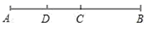19. 欢欢观察“抖空竹”时发现，可以将某一时刻的情形抽象成数学问题：如图，已知AB∥CD，∠BAE＝92°，∠DCE＝115°，则∠E的度数是°．

查看试题解析
20. $a$ 是不为1的有理数，我们把 $\frac{1}{1 - a}$ 称为 $a$ 的差倒数，如：2的差倒数是 $\frac{1}{1 - 2} = - 1$ ， $- 1$ 的差倒数是 $\frac{1}{1 - (- 1)} = \frac{1}{2}$ ．已知 $a_{1} = - \frac{1}{3}$ ， $a_{2}$ 是 $a_{1}$ 的差倒数， $a_{3}$ 是 $a_{2}$ 的差的倒数，……，以此类推，则 $a_{3} =$ ， $a_{2024} =$ ．

查看试题解析

三、（本大题共3个小题，每小题9分，共27分）

21. 计算： $12 + 4 \times (- 3) - 8 \div (- 2)$ ．

查看试题解析
22. 计算： $2 (3 a^{2} + a b - 2 b^{2}) - (6 a^{2} - 4 b^{2})$ ．

查看试题解析
23. 如图，点C在直线 $A B$ 上方，按下列要求画图并填空：

(1)、连结线段 $A C$ ；

(2)、过点C作直线 $A B$ 的垂线段 $C D$ ，垂足为点D；

(3)、过点B作直线 $B F ∥ A C$ ；

(4)、点C到点A的距离是线段的长度，点C到直线 $A B$ 的距离是线段的长度．

查看试题解析

四、（本大题共3个小题，每小题9分，共27分）

24. 计算： $[{(- 1)}^{2022} - \frac{2}{3}] \div \frac{1}{6} + {(- 3)}^{2} \times | - 1 | - {(- 2)}^{3}$ ．

查看试题解析
25. 先化简，再求值： $4 a^{3} - 3 (2 a^{3} b + a^{2} b) + [3 a^{2} b - 2 (3 a^{3} b + 2 a^{3} - 1)]$ ，其中 ${(a - \frac{1}{2})}^{2} + | b + 1 | = 0$ ．

查看试题解析
26. 请把以下证明过程补充完整，并在下面的括号内填上推理理由：已知：如图， $∠ 1 = ∠ 2 ， ∠ A = ∠ D$ ，则 $A B$ 与 $C D$ 平行吗？
解：∵ $∠ 1 = ∠ 2$ （已知），
又∵ $∠ 1 = ∠ 3$ （    ），
∴ $∠ 2 =$      ▲     （等量代换）．
∴ $A E ∥ F D$ （    ），
∴ $∠ A = ∠ B F D$ （    ）．
∵ $∠ A = ∠ D$ （已知），
∴ $∠ B F D =$      ▲  （等量代换），
∴ $A B ∥ C D$ （    ）．

查看试题解析

五、（本大题共2个小题，每小题9分，共18分）

27. 某班将买一些乒乓球和乒乓球拍，现了解情况如下：甲、乙两家出售同样品牌的乒乓球和乒乓球拍，乒乓球拍每副定价40元，乒乓球每盒10元．经洽谈后，甲店每买一副球拍赠送一盒乒乓球；乙店全部按定价的9折优惠．该班需购买球拍6副，乒乓球 $x$ $(x > 6)$ 盒．

(1)、用代数式表示：在甲店购买需付款元；在乙店购买需付款元；

(2)、当购买乒乓球盒数为20盒时，到哪家商店购买比较合算？请说明理由．

查看试题解析
28. 已知：如图， $E F$ $∥$ $C D$ ， $∠ 1 + ∠ 2 = 180 °$ .

(1)、判断GD和CA的位置关系，并说明理由

(2)、若DG平分 $∠ C D B$ ，且 $∠ A C D = 40 °$ ，求 $∠ A$ 的度数.

查看试题解析

六、（本大题共2个小题，每小题9分，共18分）

29. 阅读：如图，已知数轴上有A、B、C三点，它们表示的数分别是 $- 18 ， - 8 ， 8$ ．点A到点C的距离用 $A C$ 表示，计算方法：点C表示的数8，点A表示的数 $- 18$ ， $8 > - 18$ ，用 $8 - (- 18)$ ，用式子表示为： $A C = 8 - (- 18) = 26$ ．根据阅读完成下列问题：

(1)、应用： $A B =$ ， $B C =$ ；

(2)、拓展：若点C沿数轴向右以每秒9个单位长度的速度运动，则 $t$ 秒时，点C走到的位置所对应的数是，此时 $A C =$ （用含 $t$ 的代数式表示）；

(3)、探究：若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒4个单位长度和9个单位长度的速度向右运动，请问： $B C - A B$ 的值是否随着时间 $t$ 的变化而改变？若变化，请说明理由；若不变，请求其值．

查看试题解析
30.   阅读并补充下面推理过程：

(1)、如图1，已知点A是BC外一点，连接AB ， AC ．
求∠BAC+∠B+∠C的度数．
解：过点A作ED∥BC ，所以∠B=     ▲  ，∠C=     ▲  ．
又因为∠EAB+∠BAC+∠DAC=180°．
所以∠B+∠BAC+∠C=180°．

(2)、方法运用：如图2，已知AB∥ED ，求∠B+∠BCD+∠D的度数．

(3)、深化拓展：已知AB∥CD ，点C在点D的右侧，∠ADC=70°，BE平分∠ABC ， DE平分∠ADC ， BE ， DE所在的直线交于点E ，点E在AB与CD两条平行线之间．
①.如图3，点B在点A的左侧，若∠ABC=60°，则∠BED的度数为▲  °．
②.如图4，点B在点A的右侧，且AB＜CD ， AD＜BC ．若∠ABC=n°，则∠BED的度数为▲  °．（用含n的代数式表示）

查看试题解析