四川省达州市宣汉县2023-2024学年八年级上学期数学期末考试试卷

试卷更新日期：2024-04-16 类型：期末考试

进入出卷网下载

一、选择题（本大题共10个小题，每小题4分，共40分，每小题均有四个选项，其中只有一项符合题目要求。）

1. 下列各组线段中，不能构成直角三角形的是（　　）

A、3，4，5 B、5，12，13 C、6，7，9 D、8，15，17

查看试题解析
2. 在 $\frac{7}{22} ， 3.33 ， \frac{π}{2} ， - 2 \frac{1}{2} ， 0 ， 0.454455444555 . . . . . . ， \sqrt[3]{\frac{1}{27}} ， - \sqrt{0.9} ， 127$ 中，无理数的个数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
3. 在平面直角坐标系中，点 $P (2 ， - 3)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 估算 $\sqrt{31}$ 的大小在下列哪个数之间（）

A、5与5.5 B、5.5与6 C、6与6.5 D、6.5与7

查看试题解析
5. 下列命题中的真命题是（）

A、无理数的相反数是有理数 B、相等的角是对顶角 C、如果一个数有立方根，那么它一定有平方根 D、内错角相等，两直线平行

查看试题解析
6. 已知直线y＝x﹣2与y＝mx﹣n相交于点M（3，b），则关于x ， y的二元一次方程组 ${\begin{array}{l} y + 2 = x \\ m x - y = n \end{array}$ 的解为（）

A、 ${\begin{array}{l} x = 3 \\ y = 1 \end{array}$ B、 ${\begin{array}{l} x = 1 \\ y = 3 \end{array}$ C、 ${\begin{array}{l} x = 1 \\ y = - 1 \end{array}$ D、 ${\begin{array}{l} x = 3 \\ y = 5 \end{array}$

查看试题解析
7. 已知函数 $y = (m + 1) x^{m^{2} - 3}$ 是正比例函数，且图像在第二、四象限内，则 $m$ 的值是（）

A、2 B、 $- 2$ C、 $\pm 2$ D、 $- \frac{1}{2}$

查看试题解析
8. 如图，给出下列条件.① $∠ 3 = ∠ 4$ ；② $∠ 1 = ∠ 2$ ；③ $∠ 4 + ∠ B C D = 180 °$ ，且 $∠ D = ∠ 4$ ；④ $∠ 3 + ∠ 5 = 180 °$ 其中，能推出 $A D ∥ B C$ 的条作为（）

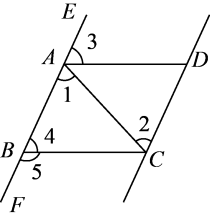A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析
9. 小锦和小丽购买了价格分别相同的中性笔和笔芯，小锦买了20支笔和2盒笔芯，用了56元；小丽买了2支笔和3俞笔芯，仅用了28元.设每支中性笔x元和每盒笔芯y元，根据题意列方程组正确的是（）

A、 ${\begin{array}{l} 2 x + 20 y = 56 \\ 2 x + 3 y = 28 \end{array}$ B、 ${\begin{array}{l} 20 x + 2 y = 56 \\ 2 x + 3 y = 28 \end{array}$ C、 ${\begin{array}{l} 20 x + 2 y = 28 \\ 2 x + 3 y = 56 \end{array}$ D、 ${\begin{array}{l} 2 x + 2 y = 28 \\ 20 x + 3 y = 56 \end{array}$

查看试题解析
10. 如图①，在边长为 $4 c m$ 的正方形 $A B C D$ 中，点 $P$ 以每秒 $2 c m$ 的速度从点 $A$ 出发，沿 $A B \to B C$ 的路径运动，到点 $C$ 停止．过点 $P$ 作 $P Q ∥ B D$ ， $P Q$ 与边 $A D$ （或边 $C D$ ）交于点 $Q$ ， $P Q$ 的长度 $y (c m)$ 与点 $P$ 的运动时间 $x$ （秒）的函数图象如图②所示．当点 $P$ 运动 $2.5$ 秒时， $P Q$ 的长是（）．

A、 $2 \sqrt{2} c m$ B、 $3 \sqrt{2} c m$ C、 $4 \sqrt{2} c m$ D、 $5 \sqrt{2} c m$

查看试题解析

二、填空题（本大题共5个小题，每小题4分，共20分）

11. $\sqrt{16}$ 的算术平方根为； $\sqrt{2}$ 的倒数是

查看试题解析
12. 已知 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ 是二元一次方程组 ${\begin{array}{l} 3 + 2 n y = m \\ n x - y = 1 - m \end{array}$ 的解，则 $n - m$ 的值是

查看试题解析
13. 如图，透明的圆柱形玻璃容器（容器厚度忽略不计）的高为 $16 c m$ ，在容器内壁离容器底部 $4 c m$ 的点B处有一滴蜂蜜，此时一只蚂蚁正好在容器外壁，位于离容器上沿 $4 c m$ 的点A处，若蚂蚁吃到蜂蜜需爬行的最短路径为 $20 c m$ ，则该圆柱底面周长为 $c m$ ．

查看试题解析
14. 如图，BP是△ABC中∠ABC的平分线，CP是∠ACB的外角的平分线，如果∠ABP=20°，∠ACP=50°，则∠A+∠P= ．

查看试题解析
15. 如图所示，已知直线 $y = - \frac{\sqrt{3}}{3} x + 1$ 与x、y轴交于B、C两点， $A (0 ， 0)$ ，在 $△ A B C$ 内依次作等边三角形，使一边在x轴上，另一个顶点在BC边上，作出的等边三角形分别是第1个 $△ A A_{1} B_{1}$ ，第2个 $△ B_{1} A_{2} B_{2}$ ，第3个 $△ B_{2} A_{3} B_{3}$ ， …则第n个等边三角形的边长等于．

查看试题解析

三、解答题（解答时应写出必要的文字说明、证明过程或演算步骤，共90分）

16. 计算

(1)、 $3 \sqrt{48} + 4 \sqrt{\frac{1}{8}} - 3 \sqrt{27}$

(2)、 ${(- \sqrt{3})}^{0} + 2^{- 2} - | - \frac{4}{4} | + {(- 2)}^{2}$

查看试题解析
17. 解下列方程组

(1)、 ${\begin{array}{l} 4 x - y = 3 \\ 3 x + 2 y = 5 \end{array}$

(2)、 ${\begin{array}{l} \frac{x}{2} + \frac{y}{3} = - 2 \\ 3 x - 4 y = 6 \end{array}$

查看试题解析
18. 已知 $2 a - 1$ 的算术平方根是3，b是8的立方根，c是 $\sqrt{13}$ 的整数部分.

(1)、求 $a + b + c$ 的值.

(2)、求 $\sqrt{a + b + 3 c}$ 的平方根.

查看试题解析
19. 在边长为1的小正方形网格中， $△ A O B$ 的顶点均在格点上，

(1)、 $B$ 点关于 $y$ 轴的对称点坐标为．

(2)、将 $△ A O B$ 向左平移3个单位长度得到 $△ A_{1} O_{1} B_{1}$ ，请画出 $△ A_{1} O_{1} B_{1}$ ；

(3)、在（2）的条件下， $A_{1}$ 的坐标为， $△ A_{1} O_{1} B_{1}$ 的面积为

查看试题解析
20. 巴川中学STEAM创新教育学部为提高学生的安全意识和安全技能，组织七、八年级学生进入区消防支队进行了实地学习和体验，并在学习结束后开展了一次消防知识竞赛．成绩分别为A、B、C、D四个等级，其中相应等级的得分依次记为10分、9分、8分、7分．学校分别从七、八年级各抽取25名学生的竞赛成绩整理并绘制成如下统计图表，请根据提供的信息解答下列问题：
年级
平均分
中位数
众数
方差
七年级
$8.76$
a
9
$1.06$
八年级
$8.76$
8
b
$1.38$

(1)、根据以上信息可以求出：a＝， b＝，并把七年级竞赛成绩统计图补充完整；

(2)、依据数据分析表，你认为七年级和八年级哪个年级的成绩更好，并说明理由；

(3)、若STEAM创新教育学部七、八年级共有800人参加本次知识竞赛，且规定9分及以上成绩为优秀，请估计该学部七、八年级参加本次知识竞赛的学生中成绩为优秀的学生共有多少人？

查看试题解析
21. 如图，在△ABC中，∠B=46°，∠C=54°，AD平分∠BAC交BC于点D，点E是边AC上一点，连接DE，若∠ADE=40°，求证：DE∥AB．

查看试题解析
22. 如图，折叠矩形的一边 $A D$ ，使点 $D$ 落在 $B C$ 边的点 $F$ 处，已知 $A B = 8 c m$ ， $B C = 10 c m$ ，求 $E C$ 的长．

查看试题解析
23. 春节即将来临，抗击新冠疫情防控工作至关重要，某公司加紧生产酒精消毒液与额温枪两种抗疫物质，其两种物资的生产成本和销售单价如表所示：

种类

生产成本（元/件）

销售单价（元/件）

酒精消毒液

56

62

额温枪

84

100

(1)、若该公司2020年12月生产两种物资共100万件，生产总成本为7280万元，请用列二元一次方程组的方法，求该月酒精消毒液和额温枪两种物资各生产了多少万件？

(2)、该公司2021年1月生产两种物资共150万件，根据市场需求，该月将举办迎新年促销活动，其中酒精消毒液的销售单价降低2元，额温枪打9折销售.若设该月生产酒精消毒液x万件，该月销售完这两种物资的总利润为y万元，求y与x之间的函数关系式.

查看试题解析
24. 阅读下列解题过程∶
$\frac{1}{\sqrt{7} + \sqrt{6}} = \frac{1 \times (\sqrt{7} - \sqrt{6})}{(\sqrt{7} + \sqrt{6}) (\sqrt{7} - \sqrt{6})} = \frac{\sqrt{7} - \sqrt{6}}{{(\sqrt{7})}^{2} - {(\sqrt{6})}^{2}} = \sqrt{7} - \sqrt{6}$
请回答下列问题∶

(1)、仿照上面的解题过程化简∶ $\frac{1}{\sqrt{6} + \sqrt{5}} =$ $=$ $=$ ．

(2)、请直接写出 $\frac{1}{\sqrt{n + 1} + \sqrt{n}}$ 的化简结果∶ ．

(3)、利用上面所提供的想法，求 $\frac{1}{1 + \sqrt{2}} + \frac{1}{\sqrt{2} + \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{4}} + . . . . . . . + \frac{1}{\sqrt{98} + \sqrt{99}} + \frac{1}{\sqrt{99} + \sqrt{100}}$ 的值．

(4)、利用上面的结论，不计算近似值，试比较 $(\sqrt{12} - \sqrt{11})$ 与 $(\sqrt{13} - \sqrt{12})$ 的大小，并说明理由．

查看试题解析
25.

【探索发现】如图1，等腰直角三角形 $A B C$ 中， $∠ A C B = 90 °$ ， $C B = C A$ ，直线 $D E$ 经过点 $C$ ，过 $A$ 作 $A D ⊥ D E$ 于点 $D$ ．过 $B$ 作 $B E ⊥ D E$ 于点 $E$ ，则 $△ B E C ≌ △ C D A$ ，我们称这种全等模型为“k型全等”．（不需要证明）

【迁移应用】已知：直线 $y = k x + 6 (k \neq 0)$ 的图象与x轴、y轴分别交于A、B两点．

(1)、如图2，当 $k = 2$ 时，在第二象限构造等腰直角 $△ A B C$ ， $∠ C A B ＝ 90 °$ ；
①直接写出 $O A =$ ， $O B =$ ；

②点C的坐标是；

(2)、如图3，当k的取值变化，点A随之在x轴负半轴上运动时，在y轴左侧过点B作 $B N ⊥ A B$ ，并且 $B N = A B$ ，连接 $O N$ ，问 $△ O B N$ 的面积是否发生变化？若不变，请求出这个定值．若变，请说明理由；

(3)、【拓展应用】如图4，在平面直角坐标系，点 $B (6 ， 4)$ ，过点B作 $A B ⊥ y$ 轴于点A，作 $B C ⊥ x$ 轴于点C，P为线段 $B C$ 上的一个动点，点 $Q (a ， 2 a - 4)$ 位于第一象限．问点A，P，Q能否构成以点Q为直角顶点的等腰直角三角形，若能，请求出a的值；若不能，请说明理由．

查看试题解析

年级	平均分	中位数	众数	方差
七年级	$8.76$	a	9	$1.06$
八年级	$8.76$	8	b	$1.38$

种类	生产成本（元/件）	销售单价（元/件）
酒精消毒液	56	62
额温枪	84	100