2023-2024学年北师大版八年级下学期数学期中仿真模拟卷二【范围:1-3章】
试卷更新日期:2024-04-15 类型:期中考试
一、选择题(每题3分,共36分)
-
1. 若等腰三角形的两边长分别为和 , 则这个三角形的周长为( )A、 B、 C、 D、或2. 下列图形中,属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如果 , 那么下列各式中正确的是( )A、 B、 C、 D、4. 如图,沿方向平移到的位置,若 , 则平移的距离是( )
3. 如果 , 那么下列各式中正确的是( )A、 B、 C、 D、4. 如图,沿方向平移到的位置,若 , 则平移的距离是( ) A、6 B、2 C、1 D、35. 下列各组数是三角形的三边,不能组成直角三角形的一组数是( )A、3,4,5 B、6,8,10 C、1.5,2,2.5 D、 , ,6. 满足-2<x≤1的数在数轴上表示为( )A、
A、6 B、2 C、1 D、35. 下列各组数是三角形的三边,不能组成直角三角形的一组数是( )A、3,4,5 B、6,8,10 C、1.5,2,2.5 D、 , ,6. 满足-2<x≤1的数在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、 7. 如图,把两根木条和的一端用螺栓固定在一起,木条自由转动至位置.在转动过程中,下面的量是常量的是( )
7. 如图,把两根木条和的一端用螺栓固定在一起,木条自由转动至位置.在转动过程中,下面的量是常量的是( )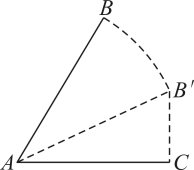 A、的度数 B、的面积 C、的长度 D、的长度8. 如图,一次函数与的图像交于点P,下列结论:①;②;③当时,;④;⑤ . 所有正确结论的序号为( ).
A、的度数 B、的面积 C、的长度 D、的长度8. 如图,一次函数与的图像交于点P,下列结论:①;②;③当时,;④;⑤ . 所有正确结论的序号为( ).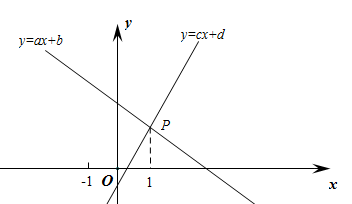 A、①②③ B、①②④ C、②③⑤ D、②④⑤9. 如图,三条公路两两相交,现计划修建一个油库,要求油库到这三条公路的距离相等,那么选择油库的位置有( )处.
A、①②③ B、①②④ C、②③⑤ D、②④⑤9. 如图,三条公路两两相交,现计划修建一个油库,要求油库到这三条公路的距离相等,那么选择油库的位置有( )处.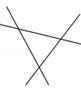 A、1 B、2 C、3 D、410. 如图,在△ABC中,已知AB=AC,BC=6cm,△CBD的周长为14cm,分别以A、B两点为圆心,大于AB的长为半径画弧,两弧相交于点M,N,连接MN与AC相交于点D,则△ACB的周长为( )
A、1 B、2 C、3 D、410. 如图,在△ABC中,已知AB=AC,BC=6cm,△CBD的周长为14cm,分别以A、B两点为圆心,大于AB的长为半径画弧,两弧相交于点M,N,连接MN与AC相交于点D,则△ACB的周长为( )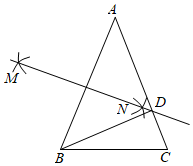 A、22cm B、16cm C、17cm D、20cm11. 铁路部门规定旅客免费携带行李箱的长、宽、高之和不超过160 cm,某厂家生产符合该规定的行李箱,已知行李箱的高为30 cm,长与宽的比为3∶2,则该行李箱的长的最大值为( )A、30 cm B、160 cm C、26 cm D、78 cm12. 如图,等边内部有一点 , , , , 在、上分别有一动点、 , 且 , 则的最小值是( )
A、22cm B、16cm C、17cm D、20cm11. 铁路部门规定旅客免费携带行李箱的长、宽、高之和不超过160 cm,某厂家生产符合该规定的行李箱,已知行李箱的高为30 cm,长与宽的比为3∶2,则该行李箱的长的最大值为( )A、30 cm B、160 cm C、26 cm D、78 cm12. 如图,等边内部有一点 , , , , 在、上分别有一动点、 , 且 , 则的最小值是( )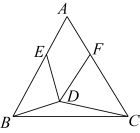 A、5 B、 C、 D、7
A、5 B、 C、 D、7二、填空题(每题4分,共20分)
-
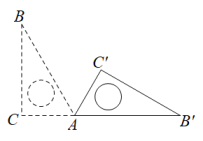
13. 等腰三角形一腰上的高与另一腰的夹角是 , 则它的底角度数是 .14. 已知点与关于原点对称,则 .15. 关于x的一元一次不等式组恰有一个整数解,则m的取值范围是 .16. 若关于y的不等式组的解集为 , 且关于x的分式方程 的解是非负整数,则所有满足条件的整数a的值之和是 .17. 如图,将直角三角板ABC绕顶点A顺时针旋转到 , 点恰好落在CA的延长线上,∠B=30°,∠C=90°,则=°
三、解答题(共7题,共64分)
-
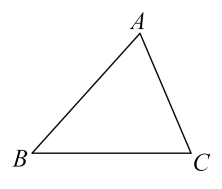
18. 解下列不等式组 , 并把它的解集表示在数轴上.19. 如图是一块三角形草坪,现要在草坪上建一个凉亭P供大家休息,且凉亭P到草坪三边的距离相等,利用直尺和圆规 , 确定凉亭P的位置.(保留作图痕迹,不写作法)
 20. 正方形的花坛内准备种植两种不同颜色的花卉,要求种植的花卉能组成轴对称或中心对称图案,下面是三种不同设计方案中的一部分,请把图1、图2补成既是轴对称图形,又是中心对称图形,并画出一条对称轴,把图3补成只是中心对称图形,并把对称中心标上字母 . (在你所设计的图案中用阴影部分和非阴影部分表示两种不同颜色的花卉.)
20. 正方形的花坛内准备种植两种不同颜色的花卉,要求种植的花卉能组成轴对称或中心对称图案,下面是三种不同设计方案中的一部分,请把图1、图2补成既是轴对称图形,又是中心对称图形,并画出一条对称轴,把图3补成只是中心对称图形,并把对称中心标上字母 . (在你所设计的图案中用阴影部分和非阴影部分表示两种不同颜色的花卉.) 21. 如图,已知直线经过点 , , 与直线交于C点、
21. 如图,已知直线经过点 , , 与直线交于C点、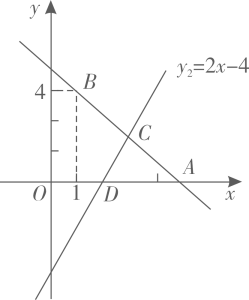 (1)、求直线的解析式以及以与x轴的交点D的坐标;(2)、求C点的坐标;(3)、根据图象,直接写出关于的不等式时x的取值范围.22. 已知:在中, .
(1)、求直线的解析式以及以与x轴的交点D的坐标;(2)、求C点的坐标;(3)、根据图象,直接写出关于的不等式时x的取值范围.22. 已知:在中, .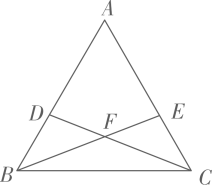 (1)、如图,点D在边上,点E在边上, , 与交于点F . 求证: ;(2)、若点D是边上的一个动点,点E是边上的一个动点,且 , 与交于点F . 当是等腰三角形时,求的度数.23. 围棋起源于中国,古代称为“弈”,是棋类鼻祖,围棋距今已有4000多年的历史,中国象棋也是中华民族的文化瑰宝,它源远流长,趣味浓厚,基本规则简明易懂.某学校为活跃学生课余生活,欲购买一批象棋和围棋,已知购买3副象棋和1副围棋共需125元,购买2副象棋和3副围棋共需165元.(1)、求每副象棋和围棋的价格;(2)、若学校准备购买象棋和围棋总共100副,且总费用不超过3200元,则最多能购买多少副围棋?24. 在学习完勾股定理这一章后,小梦和小璐进行了如下对话.
(1)、如图,点D在边上,点E在边上, , 与交于点F . 求证: ;(2)、若点D是边上的一个动点,点E是边上的一个动点,且 , 与交于点F . 当是等腰三角形时,求的度数.23. 围棋起源于中国,古代称为“弈”,是棋类鼻祖,围棋距今已有4000多年的历史,中国象棋也是中华民族的文化瑰宝,它源远流长,趣味浓厚,基本规则简明易懂.某学校为活跃学生课余生活,欲购买一批象棋和围棋,已知购买3副象棋和1副围棋共需125元,购买2副象棋和3副围棋共需165元.(1)、求每副象棋和围棋的价格;(2)、若学校准备购买象棋和围棋总共100副,且总费用不超过3200元,则最多能购买多少副围棋?24. 在学习完勾股定理这一章后,小梦和小璐进行了如下对话.小梦:如果一个三角形的三边长a,b,c满足 , 那我们称这个三角形为“类勾股三角形”,例如的三边长分别是 , 和2,因为 , 所以是“类勾股三角形”.
小璐:那等边三角形一定是“类勾股三角形”!
根据对话回答问题:
(1)、判断:小璐的说法(填“正确”或“错误”)(2)、已知的其中两边长分别为1, , 若为“类勾股三角形”,则另一边长为;(3)、如果是“类勾股三角形”,它的三边长分别为x,y,z(x,y为直角边长且 , z为斜边长),用只含有x的式子表示其周长和面积.