人教版初中数学2023-2024学年八年级下学期课时基础练习第二十章数据的分析

试卷更新日期：2024-04-15 类型：同步测试

进入出卷网下载

一、选择题

1. 已知一组数据：1，2，a，b，5，8的平均数和中位数都是4（a，b均为正整数，在去掉其中的一个最大数后，该组数据的（）

A、中位数不变 B、众数不变 C、平均数不变 D、方差不变

查看试题解析
2. 一组由小到大排列的数据为 $- 1$ ， 0，4， $x$ ， 6，16，这组数据的中位数为5，则这组数据的众数可能是 $($ 　　 $)$

A、5 B、6 C、 $- 1$ D、5.5

查看试题解析
3. 一次数学考试后，某个四人学习小组中有三个人的成绩分别为90分、90分、80分，若整个学习小组成绩的中位数为85分，则第4个同学的成绩可能为（）

A、80分 B、85分 C、90分 D、100分

查看试题解析
4. 已知一组数据x₁，x₂，x₃，平均数是2，方差是3，则另一组数2x₁-1，2x₂-1，2x₃-1的平均数和方差分别是（）

A、2， $\frac{2}{3}$ B、3，3 C、3，12 D、3，4

查看试题解析
5. 在一次献爱心的捐款活动中，某班50名同学的捐款金额如图所示，则在这次捐款活动中，该班同学捐款金额的平均数是（）

A、14.2元 B、15元 C、16.2元 D、20.25元

查看试题解析
6. 某超市销售A，B，C，D四种矿泉水，它们的单价依次是5元、3元、2元、1元，某天的销售情况如图所示，则这天销售矿泉水的平均单价是（）

A、1.95元 B、2.15元 C、2.25 元 D、2.75 元

查看试题解析
7. 已知一组数据 x₁，x₂，x₃ 的平均数是7，则 $x_{1}$ $+ 3 ， x_{2} + 2 ， x_{3} + 4$ 的平均数是（）

A、7 B、8 C、9 D、10

查看试题解析
8. 下列说法正确的是（）

A、为了解我国中学生课外阅读的情况，应采用全面调查的方式 B、一组数据1，2，5，5，5，3，3的中位数和众数都是5 C、抛掷一枚硬币200次，一定有100次"正面朝上” D、若甲组数据的方差是0.03，乙组数据的方差是0.1，则甲组数据比乙组数据稳定

查看试题解析
9. 某招聘考试规定按笔试成绩占 $60 %$ ，面试成绩占 $40 %$ 计算最终得分，小李笔试90分、面试80分；小吴笔试80分、面试90分；小叶笔试60分、面试70分，则最终得分最高的是（）

A、小李 B、小吴 C、小叶 D、小李和小吴一样最高

查看试题解析
10. 五名学生投篮训练，规定每人投10次，记录他们每人投中的次数，得到五个数据，经分析这五个数据的中位数为6，唯一众数是7，则他们投中次数占投篮总次数的百分率可能是（）

A、 $40 %$ B、 $56 %$ C、 $60 %$ D、 $62 %$

查看试题解析

二、填空题

11. 为了解“睡眠管理”落实情况，某校随机调查了46名学生每天平均睡眠时间，并将样本数据绘制成如图所示的统计图(其中有两个数据被遮盖).有以下关于睡眠时间的统计量：①平均数，②中位数，③众数，④方差，其中与被遮盖的数据无关的是(填序号).

查看试题解析
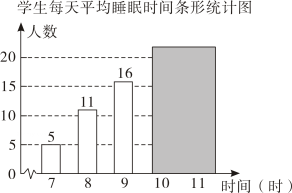12. 已知一组数据的方差计算如下： $S^{2} = \frac{1}{7} [(x_{1} - 3)$ $+ {(x_{2} - 3)}^{2} + \dots + {(x, - 3)}^{2}] ，$ ，则这组数据的和是

查看试题解析
13. 已知一组数据x₁，x₂，x₃，…，x。的方差是 1.5，则另一组数据 2x₁，2x₂， 2x₃，…，2x，的方差是.

查看试题解析
14. 两组数据： $3$ ， $x$ ， $2 y$ ， $5$ 与 $x$ ， $6$ ， $y$ 的平均数都是 $6$ ，若将这两组数据合并为一组新数据： $3$ ， $x$ ， $2 y$ ， $5$ ， $x$ ， $6$ ， $y$ ，则这组新数据的众数为．

查看试题解析
15. 我校全体师生迎“五四”诗词大赛决赛中，25名参赛同学得分情况如图所示．这些同学成绩的中位数是分．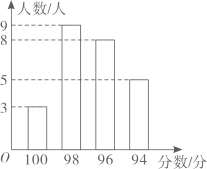

查看试题解析

三、解答题

16. 某校对八年级400名学生进行了一次体育测试，并随机抽取甲、乙两个班各50名学生的测试成绩(成绩均为整数，满分为50分)进行整理、描述和分析，制成了如下统计图表(用x表示成绩，数据分成5组：A：30≤x<34，B：34≤x<38，C：38≤x<42，D：42≤x<46，E：46≤x≤50).
班级
甲班
乙班
平均分
44.1
44.1
中位数
44.5
n
众数
m
42
方差
7.7
17.4
乙班成绩在D组的具体分数是42，42，42，42，42，42，42，42，42，42，43，44，45，45.
根据以上信息，回答下列问题：

(1)、求m，n的值.

(2)、小明这次的测试成绩是43分，在班上排名属中游略偏上，小明是甲、乙哪个班的学生?请说明理由.

(3)、假设该校八年级学生都参加此次测试，成绩达到45分及45分以上为优秀，请通过优秀率估计该校本次测试成绩优秀的学生人数.

查看试题解析
17. 学校准备从甲、乙两位选手中选择一位，代表学校参加所在地区的汉字听写大赛，总评成绩由“表达能力、阅读理解、综合素质和汉字听写”四部分组成，甲、乙两位选手的成绩(单位：分)如下表所示.
选手
表达能力
阅读理解
综合素质
汉字听写
甲
85
78
85
73
乙
73
80
82
83
请解答下列问题：

(1)、由表中成绩已算得甲的平均成绩为 80.25分，请计算乙的平均成绩.

(2)、已知四部分占总评成绩的比例如图所示.
①求图中表示“阅读理解”的扇形的圆心角度数.
②按照图中比例计算甲、乙两名选手的总评成绩，判断学校派谁参加比赛比较合适.

查看试题解析
18. 为贯彻习近平总书记提出的“绿水青山就是金山银山”的重要思想，某校举办了“绿水青山，生态文明”知识竞赛(每一项的满分为 10分，得分均为整数).在这次竞赛中张山与李仕两位同学表现优秀，他们的四项成绩分布的条形统计图如图所示，根据该图解答下列问题.
两位同学四项成绩分布的条形统计图

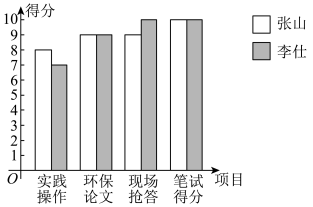(1)、完成下表：
姓名
平均数(分)
中位数(分)
众数(分)
方差(分²)
张山
9

9

李仕

9.5

1.5

(2)、根据(1)中数据，分别从中位数、方差两个角度比较分析两位同学各自的优势.

(3)、若实践操作、环保论文、现场抢答、笔试得分按4：1：2：3的比例折合成综合得分，请通过计算说明哪位同学的综合得分更高.

查看试题解析
19. 某校举行了“少年强则国强”作文大赛，并组织七、八年级各200名学生参加.现分别在七、八两个年级中各随机抽取10名学生，记录并整理了这部分学生的比赛成绩.
【收集数据】
七年级10名同学的比赛成绩分别为72，83，72，92，79，69，78，85，76，94；
八年级10名同学的比赛成绩分别为86，71，93，83，80，74，75，80，76，82.
【整理数据】
两组数据各分数段人数如下表所示：
成绩x(分)
60≤x<70
70≤x<80
80≤x<90
90≤x<100
七年级
1
5
a
2
八年级
0
4
5
1
【分析数据】
两组数据的平均数、中位数、众数、方差如下表所示：

平均数(分)
中位数(分)
众数(分)
方差(分²)
七年级
80
c
72
64.4
八年级
b
80
d
37.6
【问题解决】
根据以上信息解答下列问题：

(1)、a= ， c= ， b= ， d=.

(2)、请你估计哪个年级的比赛成绩更稳定.

(3)、按照比赛规定，90分及以上算优秀，请估计这两个年级比赛成绩达到优秀的学生人数是多少.

查看试题解析
20. 某校开展“书香校园”主题阅读活动，并实施阅读时间目标管理.为确定一个合理的目标，学校随机抽取了 30 名学生，将其一周累计主题阅读时间（单位：h）的数据作为一个样本，并对这些数据进行了收集、整理和分析，过程如下：
【数据收集】
7 8 6 5 9 10 4 6 7 5 11 12 8 7 6
4 6 3 6 8 9 10 10 13 6 7 8 3 5 10
【数据整理】
将收集的 30个数据按 A，B，C，D，E 五组进行整理统计，绘制了如图所示的不完整的条形统计图（说明：A.3≤t<5，B.5≤t<7，C.7≤t<9，D.9≤t<11，E.11≤t≤13，其中t（h）表示主题阅读时间）.
【数据分析】
统计量
平均数
众数
中位数
阅读时间（h）
7.3
m
7
请根据以上信息解答下列问题：

(1)、填空：m=.

(2)、补全条形统计图.

(3)、如果学校将目标确定为每周主题阅读时间不少于 7 h，该校有 600名学生，那么估计有多少名学生能完成目标？你认为这个目标合理吗？请说明理由.

查看试题解析

班级	甲班	乙班
平均分	44.1	44.1
中位数	44.5	n
众数	m	42
方差	7.7	17.4

选手	表达能力	阅读理解	综合素质	汉字听写
甲	85	78	85	73
乙	73	80	82	83

姓名	平均数(分)	中位数(分)	众数(分)	方差(分²)
张山	9		9
李仕		9.5		1.5

成绩x(分)	60≤x<70	70≤x<80	80≤x<90	90≤x<100
七年级	1	5	a	2
八年级	0	4	5	1

统计量	平均数	众数	中位数
阅读时间（h）	7.3	m	7