2024年重庆中考数学模拟试卷二(A卷)
试卷更新日期:2024-04-15 类型:中考模拟
一、单选题
-
1. -2的相反数为( )A、0 B、-1 C、2 D、12. 如图,这是一个由5个完全相同的小正方体组成的立体图形,它的主视图是( )
 A、
A、 B、
B、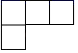 C、
C、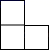 D、
D、 3. 下列函数是反比例函数的是( )A、 B、 C、 D、y=-x+54. 如果△ABC∽△DEF,且相似比为2:3,则它们对应边上的高之比为( )A、2:3 B、4:9 C、3:5 D、9:45. 如图,直线AB、CD相交于点E,DF∥AB.若∠AEC=100°,则∠D等于( )
3. 下列函数是反比例函数的是( )A、 B、 C、 D、y=-x+54. 如果△ABC∽△DEF,且相似比为2:3,则它们对应边上的高之比为( )A、2:3 B、4:9 C、3:5 D、9:45. 如图,直线AB、CD相交于点E,DF∥AB.若∠AEC=100°,则∠D等于( )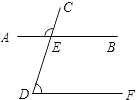 A、70° B、80° C、90° D、100°6. 估计 介于 之间.( )A、1.4与1.5 B、1.5与1.6 C、1.6与1.7 D、1.7与1.87. 希腊人常用小石子在沙滩上摆成各种形状来研究数.例如:他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16…这样的数成为正方形数.下列数中既是三角形数又是正方形数的是( )
A、70° B、80° C、90° D、100°6. 估计 介于 之间.( )A、1.4与1.5 B、1.5与1.6 C、1.6与1.7 D、1.7与1.87. 希腊人常用小石子在沙滩上摆成各种形状来研究数.例如:他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16…这样的数成为正方形数.下列数中既是三角形数又是正方形数的是( )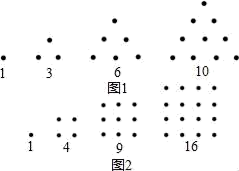 A、289 B、1024 C、1225 D、13788.
A、289 B、1024 C、1225 D、13788.如图,在平面直角坐标系中,点P在第一象限,⊙P与x轴相切于点Q,与y轴交于M(0,2),N(0,8)两点,则点P的坐标是( )
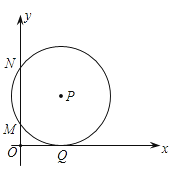 A、(5,3) B、(3,5) C、(5,4) D、(4,5)9. 如图,在正方形中,顶点在坐标轴上,且 , 以为边构造菱形 . 将菱形与正方形组成的图形绕点逆时针旋转,每次旋转 , 则第2020次旋转结束时,点的坐标为( )
A、(5,3) B、(3,5) C、(5,4) D、(4,5)9. 如图,在正方形中,顶点在坐标轴上,且 , 以为边构造菱形 . 将菱形与正方形组成的图形绕点逆时针旋转,每次旋转 , 则第2020次旋转结束时,点的坐标为( )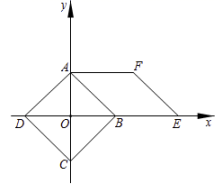 A、 B、 C、 D、10. 已知点在二次函数的图象上,其中 , 令 . 为的个位数字(为正整数),下列说法:①;②的最小值为 , 此时;③的个位数字为8.其中正确的个数是( )A、0 B、1 C、2 D、3
A、 B、 C、 D、10. 已知点在二次函数的图象上,其中 , 令 . 为的个位数字(为正整数),下列说法:①;②的最小值为 , 此时;③的个位数字为8.其中正确的个数是( )A、0 B、1 C、2 D、3二、填空题
-
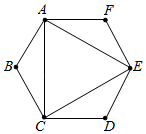
11. 计算: 的结果是 .12. 如图,正六边形 的边长为2,则 的周长为.
 13. 有三张大小、形状及背面完全相同的卡片,卡片正面分别画有正三角形、正方形、圆,从这三张卡片中任意抽取一张,卡片正面的图形既是轴对称图形又是中心对称图形的概率是.14. 某街道2020年用于绿化投资20万元,预计2022年用于绿化投资达到25万元,设这两年绿化投资的平均增长率为x , 由题意可列方程为 .15. 如图,在 中,点D、E分别 、 上的点, 与 交于点O . 给出下列三个条件:① ;② ;③ .利用其中两个条件可以证明 是等腰三角形,这两个条件可以是 .
13. 有三张大小、形状及背面完全相同的卡片,卡片正面分别画有正三角形、正方形、圆,从这三张卡片中任意抽取一张,卡片正面的图形既是轴对称图形又是中心对称图形的概率是.14. 某街道2020年用于绿化投资20万元,预计2022年用于绿化投资达到25万元,设这两年绿化投资的平均增长率为x , 由题意可列方程为 .15. 如图,在 中,点D、E分别 、 上的点, 与 交于点O . 给出下列三个条件:① ;② ;③ .利用其中两个条件可以证明 是等腰三角形,这两个条件可以是 .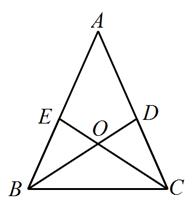 16. 六边形象征六合、六顺之意,比如首饰盒、古建筑的窗户、古井口、佛塔等等,化学上一些分子结构、物理学上的螺母,也采用六边形.从工程角度来看,正六边形是最稳定和对称的.如图,正六边形内接于 , 若正六边形的边长为6,则劣弧的长为(结果保留).
16. 六边形象征六合、六顺之意,比如首饰盒、古建筑的窗户、古井口、佛塔等等,化学上一些分子结构、物理学上的螺母,也采用六边形.从工程角度来看,正六边形是最稳定和对称的.如图,正六边形内接于 , 若正六边形的边长为6,则劣弧的长为(结果保留).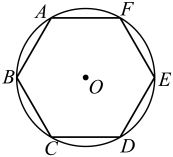 17. 已知关于 的不等式组 恰好有 个整数解,则 的取值范围为 .18. 如图, , 点是平分线上一点, , 作 , , 垂足分别为点 , , 以为边作等边三角形;作 , , 垂足分别为点 , , 以为边作等边三角形;作 , , 垂足分别为点 , , 以为边作等边三角形;…按这样的方法继续下去,则的面积为(用含正整数n的代数式表示).
17. 已知关于 的不等式组 恰好有 个整数解,则 的取值范围为 .18. 如图, , 点是平分线上一点, , 作 , , 垂足分别为点 , , 以为边作等边三角形;作 , , 垂足分别为点 , , 以为边作等边三角形;作 , , 垂足分别为点 , , 以为边作等边三角形;…按这样的方法继续下去,则的面积为(用含正整数n的代数式表示).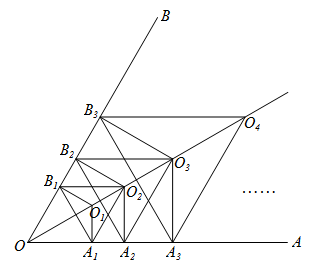
三、解答题
-
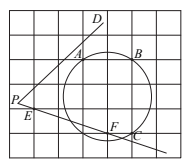
19. 计算:(1)、(x+ y)(x-y)+y(y-2)(2)、20. 如图,在每个小正方形的边长为1的网格中,圆上的点A,B,C及的一边上的点E,F均在格点上.
 (1)、线段的长等于;(2)、若点M,N分别在射线上,满足且 . 请用无刻度的直尺,在如图所示的网格中,画出点M,N,并简要说明点M,N的位置是如何找到的(不要求证明) .21. 为落实课后服务工作的相关要求,某学校于周一下午同时开设了四门特色课程供七年级学生选择(每个学生必选且只选一门):A.花样跳绳;B.趣味地理;C.创意剪纸;D.音乐欣赏.该校七年级学生共有450人,全体七年级学生的选课情况统计如图①.
(1)、线段的长等于;(2)、若点M,N分别在射线上,满足且 . 请用无刻度的直尺,在如图所示的网格中,画出点M,N,并简要说明点M,N的位置是如何找到的(不要求证明) .21. 为落实课后服务工作的相关要求,某学校于周一下午同时开设了四门特色课程供七年级学生选择(每个学生必选且只选一门):A.花样跳绳;B.趣味地理;C.创意剪纸;D.音乐欣赏.该校七年级学生共有450人,全体七年级学生的选课情况统计如图①.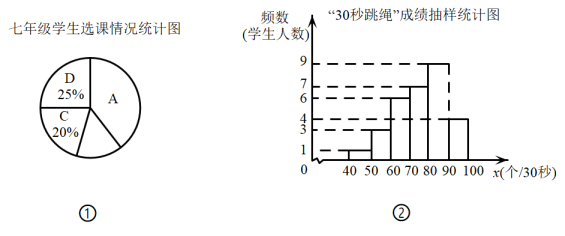 (1)、求该校七年级学生中选择A课程的学生共有多少人?(2)、为了解A课程的学习效果,对七年级选择A课程的所有学生进行了一次“30秒跳绳”成绩检测,并从中随机抽取了30名学生的“30秒跳绳”成绩进行统计,将他们的成绩绘制成频数分布直方图(如图②).
(1)、求该校七年级学生中选择A课程的学生共有多少人?(2)、为了解A课程的学习效果,对七年级选择A课程的所有学生进行了一次“30秒跳绳”成绩检测,并从中随机抽取了30名学生的“30秒跳绳”成绩进行统计,将他们的成绩绘制成频数分布直方图(如图②).①其中这一组的数据为75,72,73,74,77,77,79,则这组数据的中位数是 ▲ , 众数是 ▲ ;
②根据以上信息,估计七年级选择A课程的所有学生本次检测的“30秒跳绳”成绩超过77个的有多少人?
22. 某玩具店用2000元购进一批玩具,面市后,供不应求,于是店主又购进同样的玩具,所购的数量是第一批数量的3倍,但每件进价贵了4元,结果购进第二批玩具共用了6300元.若两批玩具的售价都是每件120元,且两批玩具全部售完。(1)、第一次购进了多少件玩具?(2)、求该玩具店销售这两批玩具共盈利多少元?23. 如图,一次函数 的图象交x轴于点A,交y轴于点B,点C在线段 上(不与点A,B重合),过点C分别作 , 的垂线,垂足为D,E,设矩形 的面积为S,点C的横坐标为x.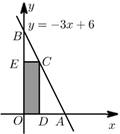 (1)、写出S与x的函数关系式.(2)、当矩形 的面积最大时,求点C的坐标.24. 如图所示,无人机在生活中的使用越来越广泛,小明用无人机测量大楼的高度.无人机悬停在空中处,测得楼楼顶的俯角是 , 楼的楼顶的俯角是 , 已知两楼间的距离米,楼的高为10米,从楼的处测得楼的处的仰角是、、、、在同一平面内).
(1)、写出S与x的函数关系式.(2)、当矩形 的面积最大时,求点C的坐标.24. 如图所示,无人机在生活中的使用越来越广泛,小明用无人机测量大楼的高度.无人机悬停在空中处,测得楼楼顶的俯角是 , 楼的楼顶的俯角是 , 已知两楼间的距离米,楼的高为10米,从楼的处测得楼的处的仰角是、、、、在同一平面内).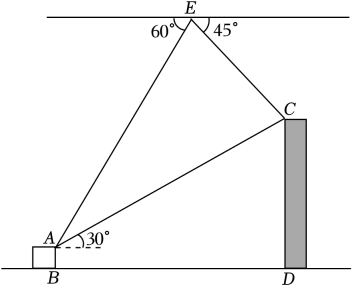 (1)、求楼的高;(2)、小明发现无人机电量不足,仅能维持60秒的飞行时间,为了避免无人机掉落砸伤人,站在点的小明马上控制无人机从处匀速以5米秒的速度沿方向返航,无人机能安全返航吗?25. 如图,抛物线 的对称轴是直线 ,与轴相交于 , 两点,与 轴交于点 ,点 的坐标为 .
(1)、求楼的高;(2)、小明发现无人机电量不足,仅能维持60秒的飞行时间,为了避免无人机掉落砸伤人,站在点的小明马上控制无人机从处匀速以5米秒的速度沿方向返航,无人机能安全返航吗?25. 如图,抛物线 的对称轴是直线 ,与轴相交于 , 两点,与 轴交于点 ,点 的坐标为 .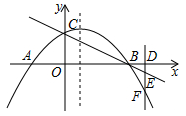 (1)、求抛物线的解析式;(2)、若点 是第四象限内抛物线上一点,过点 作 轴于点 ,交直线 于点 ,当 时,求四边形 的面积;(3)、在(2)的条件下,若点 在抛物线上,点 在抛物线的对称轴上,是否存在以点 , , , 为顶点的四边形是平行四边形?若存在,请求出所有符合条件的点 的坐标;若不存在,请说明理由.26. 在Rt△ABC中,∠A=90°,AB= AC,BC=6.
(1)、求抛物线的解析式;(2)、若点 是第四象限内抛物线上一点,过点 作 轴于点 ,交直线 于点 ,当 时,求四边形 的面积;(3)、在(2)的条件下,若点 在抛物线上,点 在抛物线的对称轴上,是否存在以点 , , , 为顶点的四边形是平行四边形?若存在,请求出所有符合条件的点 的坐标;若不存在,请说明理由.26. 在Rt△ABC中,∠A=90°,AB= AC,BC=6.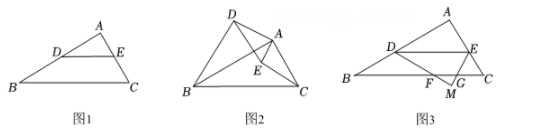 (1)、如图1,D是AB上一点,DE∥BC,交AC于E点,则BD,CE的数量关系为;(2)、如图2,将(1)中△ADE绕着点A顺时针旋转,旋转角为α(0°<α<90°),连接CE,BD,请问(1)中BD,EC的数量关系还成立吗?说明理由;(3)、如图3,将(1)中△ADE沿DE对折,A的对应点是M,使点M在BC下方,△MDE与Rt△ABC重叠部分面积记为y,BD的长记为x,求y关于x的函数关系式,并求y的最大值.
(1)、如图1,D是AB上一点,DE∥BC,交AC于E点,则BD,CE的数量关系为;(2)、如图2,将(1)中△ADE绕着点A顺时针旋转,旋转角为α(0°<α<90°),连接CE,BD,请问(1)中BD,EC的数量关系还成立吗?说明理由;(3)、如图3,将(1)中△ADE沿DE对折,A的对应点是M,使点M在BC下方,△MDE与Rt△ABC重叠部分面积记为y,BD的长记为x,求y关于x的函数关系式,并求y的最大值.