2023-2024学年沪科版初中数学八年级上册 15.3等腰三角形 同步分层训练 培优卷
试卷更新日期:2024-04-15 类型:同步测试
一、选择题
-
1. 下列条件中不能确定是等腰三角形的是( )A、三条边都相等的三角形 B、有一个锐角是45°的直角三角形 C、一个外角的平分线平行于三角形一边的三角形 D、一条中线把面积分成相等的两部分的三角形2. 如图,在中,是的角平分线,过点分别作 , 垂足分别是点E,F,则下列结论错误的是( )
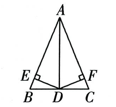 A、∠ADC=90° B、 C、 D、3. 如图,分别以A,B为圆心,大于的长度为半径作弧,交点分别为M,N,连接MN交AC于点 , 下列说法一定正确的是( )
A、∠ADC=90° B、 C、 D、3. 如图,分别以A,B为圆心,大于的长度为半径作弧,交点分别为M,N,连接MN交AC于点 , 下列说法一定正确的是( ) A、是直角三角形 B、是等腰三角形 C、是等腰三角形 D、是等腰三角形4. 在△ABC和中,.已知 , 则( )A、 B、 C、或 D、或5. 如图,在等边△PQB中,点A为PQ上一动点(不与P,Q重合),再以AB为边作等边△ABC,连接PC.有以下结论:①PB平分∠ABC;②AQ=CP;③PC//QB;④PB=PA+PC;⑤当 BC⊥BQ时,△ABC的周长最小,其中一定正确的有( )
A、是直角三角形 B、是等腰三角形 C、是等腰三角形 D、是等腰三角形4. 在△ABC和中,.已知 , 则( )A、 B、 C、或 D、或5. 如图,在等边△PQB中,点A为PQ上一动点(不与P,Q重合),再以AB为边作等边△ABC,连接PC.有以下结论:①PB平分∠ABC;②AQ=CP;③PC//QB;④PB=PA+PC;⑤当 BC⊥BQ时,△ABC的周长最小,其中一定正确的有( )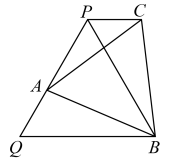 A、①②③ B、②③④ C、③④⑤ D、②③④⑤6. 如图,在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 点是线段的中点,点是轴上的一个动点,连接 , 以为直角边,点为直角顶点作等腰直角 , 连接 . 则长度的最小值是( )
A、①②③ B、②③④ C、③④⑤ D、②③④⑤6. 如图,在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 点是线段的中点,点是轴上的一个动点,连接 , 以为直角边,点为直角顶点作等腰直角 , 连接 . 则长度的最小值是( )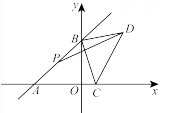 A、1 B、2 C、 D、37. 如图, , , , 分别平分的内角 , 外角 , 外角 . 以下结论:①;②;③;④和都是等腰三角形.其中正确的结论有( )
A、1 B、2 C、 D、37. 如图, , , , 分别平分的内角 , 外角 , 外角 . 以下结论:①;②;③;④和都是等腰三角形.其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个8. 如图,是等边三角形,D、E分别是的边、上的点,且 , 与相交于点P,于点F, , , 则的长为( )
A、1个 B、2个 C、3个 D、4个8. 如图,是等边三角形,D、E分别是的边、上的点,且 , 与相交于点P,于点F, , , 则的长为( ) A、8 B、13 C、16 D、17
A、8 B、13 C、16 D、17二、填空题
-
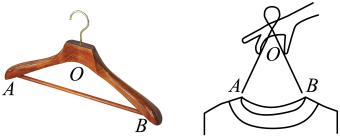
9. 由于木质的衣架没有柔性,在挂置衣服的时候不太方便操作.小敏设计了一种衣架,在使用时能轻易收拢,然后套进衣服后松开即可.如图1,衣架杆 . 若衣架收拢时, , 如图2,则此时A , B两点间的距离是cm.
 10. 如图,在中, , , D是AB上一点,且 , E是BC上一点,把沿DE翻折得 , 线段与BC交于点F,当所在的直线与的一边垂直时,DF的长是 .
10. 如图,在中, , , D是AB上一点,且 , E是BC上一点,把沿DE翻折得 , 线段与BC交于点F,当所在的直线与的一边垂直时,DF的长是 . 11. 如图,是直线上一点, , 平分 , 交于点 , , 于点 , 则 .
11. 如图,是直线上一点, , 平分 , 交于点 , , 于点 , 则 .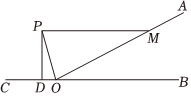 12. 如图,在△ABC中,∠C=60°,AC=5,BC=4,点D为CB延长线上一点.当点D在CB延长线上运动时,AD-BD的最小值为 .
12. 如图,在△ABC中,∠C=60°,AC=5,BC=4,点D为CB延长线上一点.当点D在CB延长线上运动时,AD-BD的最小值为 . 13. 如图,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交点于 ,且 ,以 为边长作等边三角形 ,过点 作 平行于 轴,交直线 于点 ,以 为边长作等边三角形 ,过点 作 平行于 轴,交直线 于点 ,以 为边长作等边三角形 ,…,按此规律进行下去,则点 的横坐标是.
13. 如图,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交点于 ,且 ,以 为边长作等边三角形 ,过点 作 平行于 轴,交直线 于点 ,以 为边长作等边三角形 ,过点 作 平行于 轴,交直线 于点 ,以 为边长作等边三角形 ,…,按此规律进行下去,则点 的横坐标是.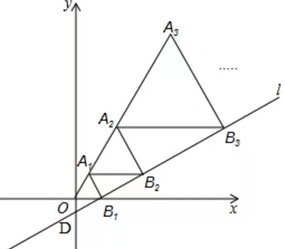
三、解答题
-
14. 如图,在中, , , 点D为内部一点,且.
 (1)、连接BD,求证:;(2)、若 , 延长AD至点E,使.
(1)、连接BD,求证:;(2)、若 , 延长AD至点E,使.①求证:DE平分;
②在DE上截取DF,使 , 连接BF,请判断EF,CD的数量关系,并给出证明.
15. 如图,∠BCD=90°,BC=CD , CD⊥AD , AC、BD交于点E , DA=DE , BN平分∠DBC , 交AC于点M , 交DC于点N . (1)、求∠ACD的度数;(2)、求证:DB=DA+DC;(3)、求证:AE=2MN .
(1)、求∠ACD的度数;(2)、求证:DB=DA+DC;(3)、求证:AE=2MN .四、综合题

