2023-2024学年沪科版初中数学七年级下册 7.2 一元一次不等式 同步分层训练 培优卷

试卷更新日期：2024-04-15 类型：同步测试

进入 出卷网 下载

一、选择题

  • 1. 若关于x ， y的二元一次方程组{x−3y=4m−13x+5y=5的解满足x+y≤0 ， 则m的取值范围是（ ）
    A、m≤2 B、m<2 C、m>2 D、m≥2

    查看试题解析

  • 2. 某业主贷款2.2万元购进一台机器，生产某种产品．已知产品的成本是每个5元，售价是每个8元，应付的税款和其他费用是售价的10%，若每个月能生产、销售2000个产品，问至少几个月后能赚回这台机器的贷款？（    ）
    A、4 B、5 C、6 D、7

    查看试题解析

  • 3. 不等式组的解集在数轴上表示如图所示，则该不等式组可能为（ ）

    A、{x≤2x>−1 B、{x<2x≥−1 C、{x≤2x≥−1 D、{x≥2x<−1

    查看试题解析

  • 4. m，n为实数，若关于x、y的方程组 {x−my=2n2x+3y=5无解，则关于a的不等式ma＞1n2的解集是（　　）
    A、a＞-13 B、a＞-3 C、a＜-13 D、a＜-3

    查看试题解析

  • 5. 在数轴上表示不等式组{x<2x>1的解集，其中正确的是（   ）
    A、 B、 C、 D、

    查看试题解析

  • 6. 关于 x 的不等式 (m+1)x≥m+1 ，下列说法正确的是（    ）
    A、解集为 x≥1 B、解集为 x≤1 C、解集为 x 取任何实数 D、无论 m 取何值，不等式肯定有解

    查看试题解析

  • 7. 已知不等式4x-a≤0的正整数解是1，2，则a的取值范围是（  ）
    A、8＜a＜12 B、8≤a＜12 C、8＜a≤12 D、8≤a≤12

    查看试题解析

  • 8. 某商品的标价比成本价高m%，根据市场需要，该商品需降价n%出售，为了不亏本，n应满足（   ）
    A、n≤m B、n≤ 100m100+m C、n≤ m100+m D、n≤ 100m100−m

    查看试题解析

二、填空题

  • 9. 某大型超市从生产基地购进一批水果，运输及销售中估计有10%的苹果正常损耗，苹果的进价是每千克2.7元，商家要避免亏本，需把售价至少定为元/千克．

    查看试题解析

  • 10. 对于任意实数a，b，都有a⊗b=a(a-b)+1，例如：3⊗2=3×(3-2)+1=4，那么不等式2⊗x≥3的非负整数解是.

    查看试题解析

  • 11. 已知△ABC是等腰三角形，它的底边长为6cm ， 则它的腰长x的取值范围是 ．

    查看试题解析

  • 12. 某同学到学校食堂买饭，看到1号、2号两个窗口前排队的人一样多（设为a人，a>8），就站到1号窗口队伍的后面，过了2分钟，他发现1号窗口每分钟有4人买饭离开，2号窗口每分钟有6人买饭离开且2号窗口后面每分钟增加5人。若此时该同学迅速从1号窗口队伍转移到2号窗口队伍后面重新排队，且到达2号窗口所花的时间比继续在1号窗口排队到达1号窗口所花的时间少（不考虑其它因素），则a的最小值为。

    查看试题解析

  • 13. 设[x]表示不超过x的最大整数{例如：[3]=3 ， [−5]=−5 ， [2.5]=2 ， [−2.7]=−3请你认真理解[x]的意义，当0<a<1 ， 若[a+180]+[a+280]+⋯+[a+7880]+[a+7980]=32 ， 则[10a]的值为 ．

    查看试题解析

三、解答题

  • 14. 2022年北京冬奥会掀起“一墩难求”热潮，由于供货紧张，某商场第一次采购雪容融10个和冰墩墩15个，采购总价为510元，第二次采购冰墩墩20个，采购雪容融数量是冰墩墩的34 ， 采购总价720元．
    (1)、雪容融和冰墩墩的进货单价各是多少元？
    (2)、商家决定采购冰墩墩的数量比雪容融数量的32倍多15个，在采购总价不超过1290元的情况下，冰墩墩最多能购进多少个？

    查看试题解析

  • 15. 十字形的路口，东西、南北方向的行人车辆来来往往，车水马龙．为了不让双方挤在一起，红绿灯就应动而生，一个方向先过，另一个方向再过．如在南稍门的十字路口，红灯绿灯的持续时间是不同的，红灯的时间总比绿灯长．即当东西方向的红灯亮时，南北方向的绿灯要经过若干秒后才亮．这样方可确保十字路口的交通安全．

    那么，如何根据实际情况设置红绿灯的时间差呢？

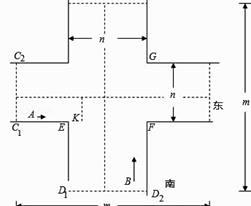
    如图所示，假设十字路口是对称的，宽窄一致．设十字路口长为m米，宽为n米．当绿灯亮时最后一秒出来的骑车人A，不与另一方向绿灯亮时出来的机动车辆B相撞，即可保证交通安全．

    根据调查，假设自行车速度为4m/s，机动车速度为8m/s．若红绿灯时间差为t秒．通过上述数据，请求出时间差t要满足什么条件时，才能使车人不相撞．当十字路口长约64米，宽约16米，路口实际时间差t=8s时，骑车人A与机动车B是否会发生交通事故？

    查看试题解析

四、综合题

  • 16. 骑行过程中佩戴安全头盔，可以保护头部，减少伤害．某商店经销甲、乙两种安全头盔，下表是近两天的销售情况：                                                                                                                                      

    时间

    甲头盔销量（个）

    乙头盔销量（个）

    销售额（元）

    第一天

    10

    15

    1150

    第二天

    6

    12

    810
    (1)、求甲、乙两种头盔的销售单价．
    (2)、若甲、乙两种安全头盔的进价分别为40元/个、30元/个，商店准备用不超过3400元的资金，再购进这两种头盔共100个．

    ①最多能购进甲种头盔多少个？

    ②商店销售完这100个头盔能否实现利润为1300元的目标？若能，请给出相应的进货方案；若不能，请说明理由．（注：利润=售价-进价，进价、售价均保持不变．）

    查看试题解析

  • 17. 某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇，下表是近两周的销售情况：                                                                                                                                                         

    销售时段

    销售数量

    销售收入

             A种型号

             B种型号

    第一周

    3台

    4台

    1200元

    第二周

    5台

    6台

    1900元

    （进价、售价均保持不变，利润=销售收入－进货成本）

    (1)、求A、B两种型号的电风扇的销售单价；
    (2)、超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台，

    ①求A种型号的电风扇最多能采购多少台？

    ②若超市销售完这50台电风扇能实现利润超过1850元的目标，有几种采购方案？

    查看试题解析