2023-2024学年湖北省七年级下学期数学期中仿真模拟卷三
试卷更新日期:2024-04-14 类型:期中考试
一、选择题(共10小题,每小题3分,共30分)
-
1. 下列实数中,最大的一个数是( )A、-5 B、 C、 D、2. 计算:的平方根等于( )A、 B、 C、 D、3. 下列命题是真命题的有( )
( 1 )相等的角是对顶角;(2)两条直线被第三条直线所截,同位角相等;(3)在同一平面内,过两点有且只有一条直线与已知直线垂直;(4)经过直线外一点,有且只有一条直线与已知直线平行;(5)一个角的余角一定大于这个角.
A、0个 B、1个 C、2个 D、3个4. 在平面直角坐标系中,点A(x,y),B(3,4),AB=5,且AB∥x轴,则A点坐标为( )A、(﹣3,4) B、(8,4) C、(3,9)或(﹣2,4) D、(﹣2,4)或(8,4)5. 如图,下列说法错误的是( ) A、因为 , 所以 B、因为 , 所以 C、因为 , 所以 D、因为 , 所以6.
A、因为 , 所以 B、因为 , 所以 C、因为 , 所以 D、因为 , 所以6.如图,点A、D在射线AE上,直线AB∥CD,∠CDE=140°,那么∠A的度数为( )
 A、140° B、60° C、50° D、40°7. 在平面直角坐标系中,横、纵坐标都是整数的点称为整点,已知 , , n为正整数,且线段AB上共有2024个整点,则n的值是( )A、1348 B、1349 C、1011 D、10128. 如图,已知AB∥CD, , .则 与 之间满足的数量关系是( )
A、140° B、60° C、50° D、40°7. 在平面直角坐标系中,横、纵坐标都是整数的点称为整点,已知 , , n为正整数,且线段AB上共有2024个整点,则n的值是( )A、1348 B、1349 C、1011 D、10128. 如图,已知AB∥CD, , .则 与 之间满足的数量关系是( ) A、 B、 C、 D、9. 如图,平面直角坐标系中,长方形的四个顶点坐标分别为 , , , , 点P从点A出发,沿长方形的边顺时针运动,速度为每秒2个长度单位,点Q从点A出发,沿长方形的边逆时针运动,速度为每秒3个长度单位,记P,Q在长方形边上第1次相遇时的点为 , 第二次相遇时的点为 , 第三次相遇时的点为 , ……,则点的坐标为( )
A、 B、 C、 D、9. 如图,平面直角坐标系中,长方形的四个顶点坐标分别为 , , , , 点P从点A出发,沿长方形的边顺时针运动,速度为每秒2个长度单位,点Q从点A出发,沿长方形的边逆时针运动,速度为每秒3个长度单位,记P,Q在长方形边上第1次相遇时的点为 , 第二次相遇时的点为 , 第三次相遇时的点为 , ……,则点的坐标为( ) A、 B、 C、 D、10. 如图1,当光从空气进入水中时,会发生折射,满足入射角∠1 与折射角∠2 的度数比为4:3.如图2,在同一平面上,两条光线同时从空气进入水中,两条入射光线与水面的夹角分别为α,β,水中两条折射光线的夹角为γ,则α,β,γ三者之间的数量关系为( )
A、 B、 C、 D、10. 如图1,当光从空气进入水中时,会发生折射,满足入射角∠1 与折射角∠2 的度数比为4:3.如图2,在同一平面上,两条光线同时从空气进入水中,两条入射光线与水面的夹角分别为α,β,水中两条折射光线的夹角为γ,则α,β,γ三者之间的数量关系为( )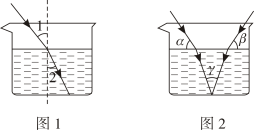 A、 B、 C、α+β=γ D、
A、 B、 C、α+β=γ D、二、填空题(共6小题,每小题3分,共18分)
-
11. 在等式中,( )内的数等于 .12. 已知 ,则 .13. 若点在x轴上,点在y轴上,则代数式的值是 .14. 为保证安全,某两段铁路两旁安置了两座可旋转探照灯A,B,探照灯的光线可看作射线如图,灯A的光线从射线开始,绕点A顺时针旋转至射线上便立即回转,灯B光线从射线开始,绕点B顺时针旋转至射线便立即回转,两灯不停交叉照射巡视.已知 , 连接 , , 则;若灯B的光线先转动,每秒转动 , 45秒后灯A的光线才开始转动,每秒转动 , 在灯B的光线第一次到达之前,灯A的光线转动秒时,两灯的光线互相平行.
 15. 在平面直角坐标系中中,线段平移至位置.若的对应点是 , 则的对应点的坐标是 .16. 如图,AB∥EG,CD∥EF,BC∥DE.若. =30°,则 z=°.
15. 在平面直角坐标系中中,线段平移至位置.若的对应点是 , 则的对应点的坐标是 .16. 如图,AB∥EG,CD∥EF,BC∥DE.若. =30°,则 z=°.
三、解答题(共8小题,共72分)
-
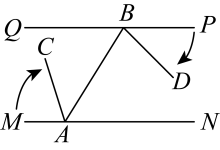
17. 求下列式子中的x的值:(1)、(2)、18. 计算:(1)、;(2)、 .19. 如图,点在上,已知 , 平分 , 平分 . 请说明的理由.
解:因为(已知),
( ),
所以( ).
因为平分 ,
所以( ).
因为平分 ,
所以 ▲ ,
得(等量代换),
所以 ▲ ( ).
20. 已知的立方根是 , 的算术平方根是4,求的平方根.21. 在如图所示的网格中,画图并填空: (1)、画出三角形ABC向右平移6个小格得到的三角形A1B1C1;(2)、画出三角形A1B1C1向下平移2个小格得到的三角形A2B2C2;(3)、如果点M是三角形ABC内一点,点M随三角形ABC经过(1)、(2)两次平移后得到的对应点是M2 , 那么线段MM2与线段AA2的位置关系是: .22. 大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,但是由于12,所以的整数部分为1,将减去其整数部分1,差就是小数部分为(1).
(1)、画出三角形ABC向右平移6个小格得到的三角形A1B1C1;(2)、画出三角形A1B1C1向下平移2个小格得到的三角形A2B2C2;(3)、如果点M是三角形ABC内一点,点M随三角形ABC经过(1)、(2)两次平移后得到的对应点是M2 , 那么线段MM2与线段AA2的位置关系是: .22. 大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,但是由于12,所以的整数部分为1,将减去其整数部分1,差就是小数部分为(1).解答下列问题:
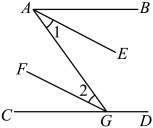
(1)、的整数部分是 , 小数部分是;(2)、如果的小数部分为a;的整数部分为b,求a+b的值;(3)、已知15x+y,出其中x是整数,且0<y<1,求x-y的相反数.23. 已知:如图,AB∥CD,EF⊥AB于点O,FG交CD于点P,当∠1=30°,求∠EFG的度数.下面提供三种思路:
思路一:过点F作MN∥CD(如图甲);
思路二:过P作PN∥EF,交AB于点N;
思路三:过O作ON∥FG,交CD于点N.

解答下列问题:
(1)、根据思路一(图甲),可求得∠EFG的度数为 ;(2)、根据思路二、三分别在图乙和图丙中作出符合要求的辅助线;(3)、请你从思路二、思路三中任选其中一种,写出求度数的解答过程.24. 如图所示, 轴于点A , 点B的坐标为 ,将线段BA沿x轴方向平移6个单位,平移后的线段为CD .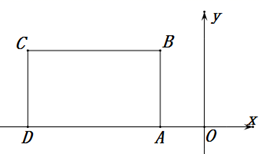 (1)、点C的坐标为;线段BC与线段AD的位置关系是;(2)、在四边形 中,点P从点A出发,沿“ ”移动,移动到点D停止.若点P的速度为每秒1个单位长度,设运动时间为t秒,回答下列问题:
(1)、点C的坐标为;线段BC与线段AD的位置关系是;(2)、在四边形 中,点P从点A出发,沿“ ”移动,移动到点D停止.若点P的速度为每秒1个单位长度,设运动时间为t秒,回答下列问题:①当点P在线段AB上运动时,若三角形ADP的面积为 ,则此时 .
②当点P在线段BC上运动时,直接写出点P在运动过程中的坐标为()(用含t的式子表示);
③在②的情况下,当四边形 的面积是四边形 面积的 时,点P的横坐标为 .